语音识别:MFCC特征参数提取
网上很多关于MFCC提取的文章,但本文纯粹我自己手码,本来不想写的,但这东西忘记的快,所以记录我自己看一个python demo并且自己本地debug的过程,在此把这个demo的步骤记下来,所以文章主要倾向说怎么做,而不是道理论述。由于python的matplotlib.pyplot库没有下载成功不会画图,文中大部分图片是我网上找的。
必备基础知知识:
1. 对数指数自然对数正弦余弦求和求积向量相乘导数一阶二阶微分
2. 矩阵及其乘法,A[i][j],i行j列,A[m][n]*B[x][y]必须满足n=x,此处为了提高用户体验度,我一般用二维数组来描述矩阵,不到万不得已我不会搬出矩阵来吓人。
3. 傅利叶变换,容易忘记,忘记就参考[傅里叶变换 掐死教程]
4. 格式为.wav的音频文件,注意注意不是.avi,.wav文件简单理解就是无损音频文件,该种格式文件可以通过c#快速编写一个录音程序得到。个人理解这种文件其实存储的是录音设备按固定频率采取的真实声波的某个点,并记录下该刻度值,从而做到从真实信号到模拟信号的转换。比如声波在实际中是一个连续的波形,但弱水三千只取一瓢饮,录音设备每隔很短的时间就取一个点,把这些点记录下来,成为离散的值,如果间隔时间足够短的话可以基本反映声音的特征。

5.采样定律,第4步说的每隔很短的时间就采取一个点,那究竟是多短?答案是大概1秒钟采取8000或16000个点,这8000和16000也叫做采样频率,采样频率需要满足真实信号最大频率处的2倍,这样可以基本真实还原声音。比如声卡采样率是8000HZ,那么可以认为原始信号的最大频率处是4000HZ,注意,原始信号的源头是声带一张一合把肺部气体排出,这一张一合的频率叫做基音频率(声音波由3个阶段,声带发出的基音频率是第一阶段;第二阶段是气体声波经过长约17cm的声道,据说第二阶段作为声音音色音质以及文本无关声纹识别中的重要部位,也是共振峰产生的场所;第三阶段是唇口鼻舌,这些部位影响声音的发音,比如元音辅音等),为了理解清晰,原始信号的频率可以默认为是声带一张一合的频率,而声卡采样频率则是1秒钟采取多少个点,所以这两者有本质的区别,但都是频率。
---------------------------------------------------------------------------------------------------------------------------
 好了,发车!
好了,发车!
一,处理.wav格式的音频文件,得到信号数据和采样频率
首先是拿到.wav格式的音频文件,其它格式比如.mp3需要进行转换,转换软件或方法有很多,不在本文讨论范围。大家很好奇该文件究竟存的什么东西,我一言以蔽之,其实除了文件头以外,就是声音波形图按照某一刻度刻画出来的离散点的值,粗暴点可以描述为信号signal = [ 0 0 -1 ..., 627 611 702],这是我自己demo的数据(接下来都以这一数据作研究)。.wav文件进行处理后就是含有107000个元素的数组,怎么从 .wav文件得到这个数组,参考python(scipy和numpy库)的(rate,signal) = scipy.io.wavfile.read("Ansel.wav"),python库的这一个方法就可以读取到.wav文件的信号数组signal和该声音文件的采样频率,此处频率rate=8000HZ。
二,预加重,{A(1*107000)}
预加重我至今没完全理解,看了一些资料,也专门加了qq群去问人,也没问到,可能我资质太低,我一直不理解时域上的采样点为啥有高低频之分,时域采样点都是固定的采样频率(8000HZ或16000HZ),所以我对下面这段话:
[语音和图像信号低频段能量大,高频段能量小...低频段信噪比大,高频信噪比低...增大高频段信噪比....]
我的理解:
这里说的高频低频是指时域上采样点分帧后的频率,针对每一帧,作傅利叶变换得到频域的N个分量,这N个分量按照频率为横坐标,振幅为纵坐标。如果没有噪音,这N个分量振幅值应该随着频率增大逐渐递减,但因为噪音存在,在某一高频段处,振幅值出现反常,变得很大,导致信噪比很小,而预加重就是为了把高频段的信号都放大,从而增大高频段的信噪比。
我的理解极有可能是错的,但我知道预加重的做法,还是以我做的demo做数据,signal = [ 0 0 -1 ..., 627 611 702]含有107000个点,预加重做法就是针对这些点,套用公式signal[i]=signal[i+1]-0.97*signal[i],因此得到一个新的数组A=[ 0. 0. -1. ..., -40.36 2.81 109.33],数组大小还是107000。系数0.97可以自己选取,据说0.95左右。
三,分帧,{B(1336*200)}
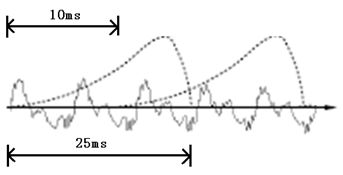
分帧原理就不说了,我说下做法:把上述数组A的元素值,200个为一帧,80个为帧移,总共可以得到1336帧,因为不是整除,1336*80+200=107080,多出的80个点用0填补,所以得到1336*200的二维数组B。
上述200个为一帧,80个为帧移是这样来的,因为默认语音信号具有短时平稳性,这平稳性不是说短时采样得到的值相等,而是认为短时间内声带、声道、唇口鼻腔这3个声音信号源头具有平稳性,据说是人体肌肉活动短时平稳。短时默认是0.025s,两个相邻短时间隔默认是0.01s,因为我分析的.wav文件是8000HZ, 所以0.025s内有0.025*8000=200个采样点,帧移0.01*8000=80个采样点。
四,加窗,{C(1336*200)}
需要一个1336*200的窗数组C,这里默认元素值都初始化为1(为了简单,用的矩形窗),实际中需用汉明窗,其实汉明窗一样道理,只不过用汉明窗的的话,这1336*200的二维数组元素值需要根据汉明窗函数计算得到。汉明窗函数是一个余弦函数,作用是为了使帧和帧之间变得平滑,消除吉布斯效应(傅利叶变换时无法得到边界值,据说是傅利叶打败拉格朗日的跨历史争执),接下来说下具体怎么加窗。
分帧后的数组B和窗函数数组C具有相同的维度,把它们对应位置的元素值相乘,即可以得到加窗后的二维数组C,C[i[j]=B[i][j]*C[i][j]],因为我用的矩形窗,C[i][j]值都为1,所以C=B。五,离散傅利叶变换(FFT),{D(1336*257),E(1336*257),F(1336*1)}
首先还是温习下[傅里叶变换 掐死教程],看完这个教程我认为,已知经过加窗后的信号C具有1336*200维,也就是说有1336行(帧),每行200个点,每相邻两行之间有120个重合点(帧移80)。那么对它做傅利叶变换,粗暴的理解为,对有1336帧,每一帧都作N=512的傅利叶变换,这个过程可以认为每一帧分解为257个分量,每个分量其实是一个正/余弦波的振幅,也就把短时的时域帧(200个点)分解为频域上的257个分量,有点像力学分解...
因此可以得到1336*257维的频域信号D,帧数还是1336,对每一帧的257个点的值(个人认为是振幅)取平方,再乘以1/512,便得到能量,这个公式我不理解,我只记得高中时有印象振幅好像代表能量,但是平方再除以512,我就不明白为啥,难道跟面积/边长计算类似?不管怎样,得到1336*257的能量普E,然后对每一帧的257个能量值简单相加,得到该帧的能量总值,一共有1336帧,于是有1336个能量总值,即拥有1336个元素值,记为数组F,数组中每个元素值代表一帧的能量总值。
六,获得梅尔滤波器{G(26*257)}
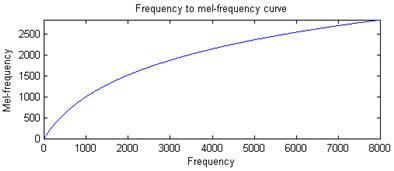
如上图,梅尔值是一个新的量度,据说相比频率量度,梅尔更接近人耳的听觉机理,通俗的说,就像纳米和米一样,如果我们用纳米衡量我们身边的事物会是一种什么感受?所以频率的某一个值对应着梅尔的某一个值,该印射关系可以用这个公式描述,梅尔值f(f)=2595*lg(1+f/700.0),如果要反过来,频率f(m)=700*(10**(m/2595.0)-1),10**(m/2595.0)意思是10的(m/2595.0)次方。我们看第一个公式,我们的采样频率除以2就是真实信号的最大频率,真实信号的最小频率为0,依据公式的单调性,我们以这个最大频率和最小频率为界限分别得到梅尔刻度的最大最小值,可以把信号的所有频率值刻画在这个梅尔区间之内。
梅尔滤波器个数一般默认26个,前期准备工作需要在上述最大最小梅尔区间等间距插入26个值,包括边界,就是28个值,然后把这28个值的频率值也算出来,得到28个频率和梅尔的一一对应关系。接下来对这28个频率值,依次代入公式y=(512+1)*x/8000),便可以得到28个y值。我不明白这个公式干嘛的,只知道,512是傅利叶变换的N,8000是采样频率,。
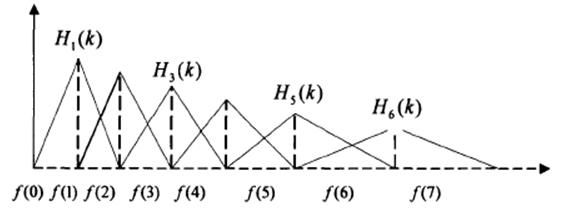
接下来计算26个滤波器的二维数组,先初始化为元素值都为0的26*257二维数组G,然后通过循环填补该二维数组的值,过程大致是针对G的每一行,根据行下标(0~25),再结合上述的28个y值,计算出每行的各个元素值,其计算过程是把相邻两个y值相减作分母,分子是每行的元素值下标减去28个元素的下标为行元素值下标的值,再用28个元素的下标为行元素值下标的值减去每行的元素值下标。针对每一行,这样可以得到三角形形状的数据分布,三角形顶点为1,除此三角形数据分布之外的点都为0,这个二维数组G经过转化之后便得到每行只有一部分有值,其余值为0的二维矩阵,而且有值部分数据呈三角形分布。此处很难解释,没图说个j*,用文字简直不可描述,还是上图来说明。如下所示,图中H1(k)是G的第一行元素值分布,H3(k)是G的第二行元素值分布,H26(k)是G的第26行元素分布,每一行都有257个元素值,比如H1(k),也就是G的第一行,只有开头几个元素值有值,其余200多个值均为0,且有值部分值大小先线形增大到1,再线性减小到0。
七,得到能量特征参数的和能量总值{H(1336*26)}
把第五步得到的二维矩阵能量谱E(1336*257),乘以第六部的二维数组梅尔滤波器G(26*257)的逆,矩阵的逆可得到257*26的矩阵,然后满足矩阵乘法定律,得到参数H=E*G.T,此处的H其实是1336*26的二维矩阵。还有个参数是第五步计算出来的每帧能量总值F(1336*1),即拥有1336个元素值的一维数组F。
八,作自然对数运算,离散余弦变换(DCT)和升倒谱运算{J(1336*13),K(13*1),L(1336*13),feat[1336*13]}
对H的每一个元素值做ln运算,即H[i][j]=ln(H[i][j]),此处我也不明白原理,但很多资料记载说需要做这一部操作,好像是什么公式。接着对feat的每一行做离散余弦变换(离散余弦变换类似傅利叶变换,只不过作用在实数范围)。据说离散余弦变换后的数据分布可以把冗余数据分开,而且大部分信号数据一般集中在变换后的低频区,所以对每一帧只取前13个数据就好了,于是得到1336*13的二维数组J。
针对1336*13的二维数组J做升倒谱操作,默认升倒谱系数为22,这个过程做法是先产生一个拥有13个元素的一维数组K,这13个元素的值K[i]=1+(22 /2)*sin(pi*i/22),其中22是升倒谱系数,pi是圆周率3.1415926。得到这个数组K之后,针对1336*13的二维数组J,J[i][j] = J[i][j]*K[j],得到1336*13的二维数组L,这其实就是mfcc参数的第一组。如果这组参数想要加上能量作为其表示方式,可以把这1336帧,也就是每一行的的第一个元素用一维数组F的每个值替换,即L[i][0] = F[i]。
我们把这经过错综复杂得到的L记为feat,它是个二维数组,拥有1336*13个值,这也是mfcc参数的基础参数,也是第一组,默认是有3组,接下来计算第二和第三组参数。
九,计算第二组和第三组参数{feat[1336*13],feat'[1336*13],feat''[1336*13]}
一言以蔽之,第二组参数其实就是在已有的基础参数下作一阶微分操作,第三组参数在第二组参数下作一阶微分操作,相当于对基础参数导数的导数。微分(dx)如果忘了,就把他理解为自变量增长为1的函数值的变化量,准确点描述是要计算离散点之间的变换率,而不是连续函数的导数,但原理类似。

具体操作是这样的,抽取一个计算一阶微分的函数,然后把1336*13的二维数组feat作为参数传入,返回feat的一阶微分feat‘,feat'同样有1336*13个元素值。这个函数有点复杂,我把python函数贴上来。我简要说两句,其实这个过程是把feat按照行作循环,每一行拥有13个元素值,如果不考虑边际效应,feat'[i][j]={feat[i][j+1]-feat[i][j-1] + 2(feat[i][j+2]-feat[i][j-2]) + 3(feat[i][j+3]-feat[i][j-3]) + ... + n(feat[i][j+n]-feat[i][j-n])} / M,M作为分母,是这个函数输入的big_theta来决定的,big_theta默认值是2,此处的M值可以算出是10,过程参照函数代码。这个公式可能还是太复杂,如果大家对一阶展开式或者泰勒展开式还有印象,对这些应该就不会陌生,上述公式可以再简化点,大概长成这样f’(x)={f(x+1)-f(x-1) + 2(f(x+2)-f(x-2)) + 3(f(x+3)-f(x-3)) + ...+ n(f(x+n)-f(x-n)) } / M,这个就平易近人了,所以此处的计算一阶微分函数,大致过程就是这样。最后得到的输出是1336*13的二维数组feat',也是mfcc参数的第二组参数。
第三组参数同上,把feat'作为参数运用抽取出来的函数作计算,得到输出记为feat'',feat''二维数组同样有1336*13个元素值,这是mfcc参数的第三组参数。
十,得到最后输出{mfcc(1336*39)}
由前八步和第九步,可以得到feat,feat'和feat'',这3个参数都是拥有1336*13个元素值的二维数组,而且这三个二维数组的每一行第一个元素值可以根据需要,用该行(帧)的能量总值替换。把feat,feat‘和feat''拼在一起,即基于feat,每一行横向追加feat'和feat''每行的元素值,得到拥有1336*39个元素值的一个二维数组,也就是mfcc系数,这就是最后得到的结果。
得到的mfcc系数,可供语音识别或声纹识别(文本无关,文本相关)等技术,但语音识别需要语料库,因此还需要建立语音模型来训练语音,经典的语音模型有HMM,新兴的有神经元模型,但不管怎样,语音模型的建立难度应该比mfcc更大...
1.对音频信号进行分割为帧
#coding=utf-8
#对音频信号处理程序
#张泽旺,2015-12-12
# 本程序主要有四个函数,它们分别是:
# audio2frame:将音频转换成帧矩阵
# deframesignal:对每一帧做一个消除关联的变换
# spectrum_magnitude:计算每一帧傅立叶变换以后的幅度
# spectrum_power:计算每一帧傅立叶变换以后的功率谱
# log_spectrum_power:计算每一帧傅立叶变换以后的对数功率谱
# pre_emphasis:对原始信号进行预加重处理
import numpy
import math
def audio2frame(signal,frame_length,frame_step,winfunc=lambda x:numpy.ones((x,))):
'''将音频信号转化为帧。
参数含义:
signal:原始音频型号
frame_length:每一帧的长度(这里指采样点的长度,即采样频率乘以时间间隔)
frame_step:相邻帧的间隔(同上定义)
winfunc:lambda函数,用于生成一个向量
'''
signal_length=len(signal) #信号总长度
frame_length=int(round(frame_length)) #以帧帧时间长度
frame_step=int(round(frame_step)) #相邻帧之间的步长
if signal_length<=frame_length: #若信号长度小于一个帧的长度,则帧数定义为1
frames_num=1
else: #否则,计算帧的总长度
frames_num=1+int(math.ceil((1.0*signal_length-frame_length)/frame_step))
pad_length=int((frames_num-1)*frame_step+frame_length) #所有帧加起来总的铺平后的长度
zeros=numpy.zeros((pad_length-signal_length,)) #不够的长度使用0填补,类似于FFT中的扩充数组操作
pad_signal=numpy.concatenate((signal,zeros)) #填补后的信号记为pad_signal
indices=numpy.tile(numpy.arange(0,frame_length),(frames_num,1))+numpy.tile(numpy.arange(0,frames_num*frame_step,frame_step),(frame_length,1)).T #相当于对所有帧的时间点进行抽取,得到frames_num*frame_length长度的矩阵
indices=numpy.array(indices,dtype=numpy.int32) #将indices转化为矩阵
frames=pad_signal[indices] #得到帧信号
win=numpy.tile(winfunc(frame_length),(frames_num,1)) #window窗函数,这里默认取1
return frames*win #返回帧信号矩阵
def deframesignal(frames,signal_length,frame_length,frame_step,winfunc=lambda x:numpy.ones((x,))):
'''定义函数对原信号的每一帧进行变换,应该是为了消除关联性
参数定义:
frames:audio2frame函数返回的帧矩阵
signal_length:信号长度
frame_length:帧长度
frame_step:帧间隔
winfunc:对每一帧加window函数进行分析,默认此处不加window
'''
#对参数进行取整操作
signal_length=round(signal_length) #信号的长度
frame_length=round(frame_length) #帧的长度
frames_num=numpy.shape(frames)[0] #帧的总数
assert numpy.shape(frames)[1]==frame_length,'"frames"矩阵大小不正确,它的列数应该等于一帧长度' #判断frames维度
indices=numpy.tile(numpy.arange(0,frame_length),(frames_num,1))+numpy.tile(numpy.arange(0,frames_num*frame_step,frame_step),(frame_length,1)).T #相当于对所有帧的时间点进行抽取,得到frames_num*frame_length长度的矩阵
indices=numpy.array(indices,dtype=numpy.int32)
pad_length=(frames_num-1)*frame_step+frame_length #铺平后的所有信号
if signal_length<=0:
signal_length=pad_length
recalc_signal=numpy.zeros((pad_length,)) #调整后的信号
window_correction=numpy.zeros((pad_length,1)) #窗关联
win=winfunc(frame_length)
for i in range(0,frames_num):
window_correction[indices[i,:]]=window_correction[indices[i,:]]+win+1e-15 #表示信号的重叠程度
recalc_signal[indices[i,:]]=recalc_signal[indices[i,:]]+frames[i,:] #原信号加上重叠程度构成调整后的信号
recalc_signal=recalc_signal/window_correction #新的调整后的信号等于调整信号处以每处的重叠程度
return recalc_signal[0:signal_length] #返回该新的调整信号
def spectrum_magnitude(frames,NFFT):
'''计算每一帧经过FFY变幻以后的频谱的幅度,若frames的大小为N*L,则返回矩阵的大小为N*NFFT
参数说明:
frames:即audio2frame函数中的返回值矩阵,帧矩阵
NFFT:FFT变换的数组大小,如果帧长度小于NFFT,则帧的其余部分用0填充铺满
'''
complex_spectrum=numpy.fft.rfft(frames,NFFT) #对frames进行FFT变换
return numpy.absolute(complex_spectrum) #返回频谱的幅度值
def spectrum_power(frames,NFFT):
'''计算每一帧傅立叶变换以后的功率谱
参数说明:
frames:audio2frame函数计算出来的帧矩阵
NFFT:FFT的大小
'''
return 1.0/NFFT * numpy.square(spectrum_magnitude(frames,NFFT)) #功率谱等于每一点的幅度平方/NFFT
def log_spectrum_power(frames,NFFT,norm=1):
'''计算每一帧的功率谱的对数形式
参数说明:
frames:帧矩阵,即audio2frame返回的矩阵
NFFT:FFT变换的大小
norm:范数,即归一化系数
'''
spec_power=spectrum_power(frames,NFFT)
spec_power[spec_power<1e-30]=1e-30 #为了防止出现功率谱等于0,因为0无法取对数
log_spec_power=10*numpy.log10(spec_power)
if norm:
return log_spec_power-numpy.max(log_spec_power)
else:
return log_spec_power
def pre_emphasis(signal,coefficient=0.95):
'''对信号进行预加重
参数含义:
signal:原始信号
coefficient:加重系数,默认为0.95
'''
return numpy.append(signal[0],signal[1:]-coefficient*signal[:-1])2.对每一帧提取39个MFCC+delta+delta_delta系数
#coding=utf-8
# 计算每一帧的MFCC系数
# 张泽旺,2015-12-13
import numpy
from sigprocess import audio2frame
from sigprocess import pre_emphasis
from sigprocess import spectrum_power
from scipy.fftpack import dct
#首先,为了适配版本3.x,需要调整xrange的使用,因为对于版本2.x只能使用range,需要将xrange替换为range
try:
xrange(1)
except:
xrange=range
def calcMFCC_delta_delta(signal,samplerate=16000,win_length=0.025,win_step=0.01,cep_num=13,filters_num=26,NFFT=512,low_freq=0,high_freq=None,pre_emphasis_coeff=0.97,cep_lifter=22,appendEnergy=True):
'''计算13个MFCC+13个一阶微分系数+13个加速系数,一共39个系数
'''
feat=calcMFCC(signal,samplerate,win_length,win_step,cep_num,filters_num,NFFT,low_freq,high_freq,pre_emphasis_coeff,cep_lifter,appendEnergy) #首先获取13个一般MFCC系数
result1=derivate(feat)
result2=derivate(result1)
result3=numpy.concatenate((feat,result1),axis=1)
result=numpy.concatenate((result3,result2),axis=1)
return result
def calcMFCC_delta(signal,samplerate=16000,win_length=0.025,win_step=0.01,cep_num=13,filters_num=26,NFFT=512,low_freq=0,high_freq=None,pre_emphasis_coeff=0.97,cep_lifter=22,appendEnergy=True):
'''计算13个MFCC+13个一阶微分系数
'''
feat=calcMFCC(signal,samplerate,win_length,win_step,cep_num,filters_num,NFFT,low_freq,high_freq,pre_emphasis_coeff,cep_lifter,appendEnergy) #首先获取13个一般MFCC系数
result=derivate(feat) #调用derivate函数
result=numpy.concatenate((feat,result),axis=1)
return result
def derivate(feat,big_theta=2,cep_num=13):
'''计算一阶系数或者加速系数的一般变换公式
参数说明:
feat:MFCC数组或者一阶系数数组
big_theta:公式中的大theta,默认取2
'''
result=numpy.zeros(feat.shape) #结果
denominator=0 #分母
for theta in numpy.linspace(1,big_theta,big_theta):
denominator=denominator+theta**2
denominator=denominator*2 #计算得到分母的值
for row in numpy.linspace(0,feat.shape[0]-1,feat.shape[0]):
tmp=numpy.zeros((cep_num,))
numerator=numpy.zeros((cep_num,)) #分子
for t in numpy.linspace(1,cep_num,cep_num):
a=0
b=0
s=0
for theta in numpy.linspace(1,big_theta,big_theta):
if (t+theta)>cep_num:
a=0
else:
a=feat[row][t+theta-1]
if (t-theta)<1:
b=0
else:
b=feat[row][t-theta-1]
s+=theta*(a-b)
numerator[t-1]=s
tmp=numerator*1.0/denominator
result[row]=tmp
return result
def calcMFCC(signal,samplerate=16000,win_length=0.025,win_step=0.01,cep_num=13,filters_num=26,NFFT=512,low_freq=0,high_freq=None,pre_emphasis_coeff=0.97,cep_lifter=22,appendEnergy=True):
'''计算13个MFCC系数
参数含义:
signal:原始音频信号,一般为.wav格式文件
samplerate:抽样频率,这里默认为16KHz
win_length:窗长度,默认即一帧为25ms
win_step:窗间隔,默认情况下即相邻帧开始时刻之间相隔10ms
cep_num:倒谱系数的个数,默认为13
filters_num:滤波器的个数,默认为26
NFFT:傅立叶变换大小,默认为512
low_freq:最低频率,默认为0
high_freq:最高频率
pre_emphasis_coeff:预加重系数,默认为0.97
cep_lifter:倒谱的升个数??
appendEnergy:是否加上能量,默认加
'''
feat,energy=fbank(signal,samplerate,win_length,win_step,filters_num,NFFT,low_freq,high_freq,pre_emphasis_coeff)
feat=numpy.log(feat)
feat=dct(feat,type=2,axis=1,norm='ortho')[:,:cep_num] #进行离散余弦变换,只取前13个系数
feat=lifter(feat,cep_lifter)
if appendEnergy:
feat[:,0]=numpy.log(energy) #只取2-13个系数,第一个用能量的对数来代替
return feat
def fbank(signal,samplerate=16000,win_length=0.025,win_step=0.01,filters_num=26,NFFT=512,low_freq=0,high_freq=None,pre_emphasis_coeff=0.97):
'''计算音频信号的MFCC
参数说明:
samplerate:采样频率
win_length:窗长度
win_step:窗间隔
filters_num:梅尔滤波器个数
NFFT:FFT大小
low_freq:最低频率
high_freq:最高频率
pre_emphasis_coeff:预加重系数
'''
high_freq=high_freq or samplerate/2 #计算音频样本的最大频率
signal=pre_emphasis(signal,pre_emphasis_coeff) #对原始信号进行预加重处理
frames=audio2frame(signal,win_length*samplerate,win_step*samplerate) #得到帧数组
spec_power=spectrum_power(frames,NFFT) #得到每一帧FFT以后的能量谱
energy=numpy.sum(spec_power,1) #对每一帧的能量谱进行求和
energy=numpy.where(energy==0,numpy.finfo(float).eps,energy) #对能量为0的地方调整为eps,这样便于进行对数处理
fb=get_filter_banks(filters_num,NFFT,samplerate,low_freq,high_freq) #获得每一个滤波器的频率宽度
feat=numpy.dot(spec_power,fb.T) #对滤波器和能量谱进行点乘
feat=numpy.where(feat==0,numpy.finfo(float).eps,feat) #同样不能出现0
return feat,energy
def log_fbank(signal,samplerate=16000,win_length=0.025,win_step=0.01,filters_num=26,NFFT=512,low_freq=0,high_freq=None,pre_emphasis_coeff=0.97):
'''计算对数值
参数含义:同上
'''
feat,energy=fbank(signal,samplerate,win_length,win_step,filters_num,NFFT,low_freq,high_freq,pre_emphasis_coeff)
return numpy.log(feat)
def ssc(signal,samplerate=16000,win_length=0.025,win_step=0.01,filters_num=26,NFFT=512,low_freq=0,high_freq=None,pre_emphasis_coeff=0.97):
'''
待补充
'''
high_freq=high_freq or samplerate/2
signal=sigprocess.pre_emphasis(signal,pre_emphasis_coeff)
frames=sigprocess.audio2frame(signal,win_length*samplerate,win_step*samplerate)
spec_power=sigprocess.spectrum_power(frames,NFFT)
spec_power=numpy.where(spec_power==0,numpy.finfo(float).eps,spec_power) #能量谱
fb=get_filter_banks(filters_num,NFFT,samplerate,low_freq,high_freq)
feat=numpy.dot(spec_power,fb.T) #计算能量
R=numpy.tile(numpy.linspace(1,samplerate/2,numpy.size(spec_power,1)),(numpy.size(spec_power,0),1))
return numpy.dot(spec_power*R,fb.T)/feat
def hz2mel(hz):
'''把频率hz转化为梅尔频率
参数说明:
hz:频率
'''
return 2595*numpy.log10(1+hz/700.0)
def mel2hz(mel):
'''把梅尔频率转化为hz
参数说明:
mel:梅尔频率
'''
return 700*(10**(mel/2595.0)-1)
def get_filter_banks(filters_num=20,NFFT=512,samplerate=16000,low_freq=0,high_freq=None):
'''计算梅尔三角间距滤波器,该滤波器在第一个频率和第三个频率处为0,在第二个频率处为1
参数说明:
filers_num:滤波器个数
NFFT:FFT大小
samplerate:采样频率
low_freq:最低频率
high_freq:最高频率
'''
#首先,将频率hz转化为梅尔频率,因为人耳分辨声音的大小与频率并非线性正比,所以化为梅尔频率再线性分隔
low_mel=hz2mel(low_freq)
high_mel=hz2mel(high_freq)
#需要在low_mel和high_mel之间等间距插入filters_num个点,一共filters_num+2个点
mel_points=numpy.linspace(low_mel,high_mel,filters_num+2)
#再将梅尔频率转化为hz频率,并且找到对应的hz位置
hz_points=mel2hz(mel_points)
#我们现在需要知道这些hz_points对应到fft中的位置
bin=numpy.floor((NFFT+1)*hz_points/samplerate)
#接下来建立滤波器的表达式了,每个滤波器在第一个点处和第三个点处均为0,中间为三角形形状
fbank=numpy.zeros([filters_num,NFFT/2+1])
for j in xrange(0,filters_num):
for i in xrange(int(bin[j]),int(bin[j+1])):
fbank[j,i]=(i-bin[j])/(bin[j+1]-bin[j])
for i in xrange(int(bin[j+1]),int(bin[j+2])):
fbank[j,i]=(bin[j+2]-i)/(bin[j+2]-bin[j+1])
return fbank
def lifter(cepstra,L=22):
'''升倒谱函数
参数说明:
cepstra:MFCC系数
L:升系数,默认为22
'''
if L>0:
nframes,ncoeff=numpy.shape(cepstra)
n=numpy.arange(ncoeff)
lift=1+(L/2)*numpy.sin(numpy.pi*n/L)
return lift*cepstra
else:
return cepstra3.测试代码
#coding=utf-8
#测试文件
from sigprocess import *
from calcmfcc import *
import scipy.io.wavfile as wav
import numpy
(rate,sig) = wav.read("wav1.wav")
mfcc_feat = calcMFCC_delta_delta(sig,rate)
print(mfcc_feat.shape)