十、表示与描述

一，背景

令S表示一幅图像中像素的子集。若S中的两个像素p,q之间存在完全由像素组成的路径，则p,q在S中是连接的。对于S中任意像素p,在S中连接到该像素的一组像素称为连接分量。若该像素仅有一个连接分量，则S称为一个连接集。图像中像素的子集R是一个连接集时，则将其称为图像的一个区域。
区域的边界定义为该区域内一组像素的集合，但这组像素有一个或多个不属于该区域的相邻像素。
提取区域及边界的函数
函数bwlabel计算二值图像中所有的连通分量（区域），调用语法为

[L,num] = bwlabel(f,conn)

其中f是输入图像，conn指定期望的连通性，num是找到的连通分量数，L是标记矩阵。

函数bwperim 产生一幅包括边界的二值图像，语法调用：

g = bwperim(f,conn)

其中，g是返回的二值图像，包含f中所有的边界像素。需要注意的是，这个函数具有特殊性，conn默认的连通数是4连通。为了获得4连通的区域边界，可以将conn指定为4；同理，为了获得8连通的区域边界，把conn设置为8即可。

函数bwboundaries用于提取二值图像f中所有区域的真实边界坐标，调用语法为：

B = bwboundaries(f,conn,options)

其中，f是二值图像，conn是8（default）或4，options可以选择’holes’（提取区域和孔洞的边界、提取包含嵌套区域的区域边界）和’noholes’（仅提取区域及其子区域的边界）。
B中先列出区域，然后列出空洞。
当输出B是P×1的单位数组时，P是物体数。单位数组中的每个单元都包含一个np×2的矩阵，其中的行是边界像素的行和列的坐标，np是相应区域的边界像素数。每个边界的坐标都是以顺时针方向安排的，并且边界的最后一点与第一点相同，这样就提供了闭合的边界。
使用函数flipud改变边界B{k}的行进顺序，从顺时针改变成逆时针，调用代码

Breversed(k) = flipud(B{k})

二，表示

1，链码

链码通过指定长度与方向的直线段的连接序列来表示边界。通常，这种表示基于这些线段4连接或者8连接。每条线段的方向使用一种数字编号方案编码，以方向性数字序列表示的编码称为弗雷曼编码。

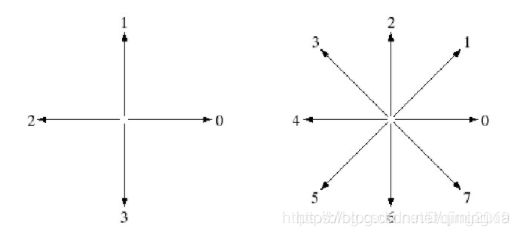
一条边界的链码取决于起点，代码可以将起点处理为方向数的循环序列和重新定义起点的方法进行归一化，因此产生最小量级的整数部分。
弗雷曼链码及其某些变化

f = imread('C:Fig1006(a).tif');
subplot(231),imshow(f),title('原始图像');
h = fspecial('average', 9);
g = imfilter(f, h ,'replicate');
subplot(232),imshow(g),title('9×9平均模板处理结果');
gB = im2bw(g,0.5);
subplot(233),imshow(gB),title('阈值处理后结果');
B = bwboundaries(gB,'noholes');
d = cellfun('length',B);
[max_d, k] = max(d);
b = B{1};
[M N] = size(g);
g = bound2im(b,M,N,min(b(:,1)),min(b(:,2)));
subplot(234),imshow(g),title('二值图像的边界图像');
[s,su] = bsubsamp(b,50);
g2 = bound2im(s,M,N);
subplot(235),imshow(g2),title('自取样的边界图像');
cn = connectpoly(s(:, 1),s(:, 2));
g3 = bound2im(cn,M,N,min(cn(:,1)),min(cn(:,2)));
subplot(236),imshow(g3),title('对上图的点进行连接');

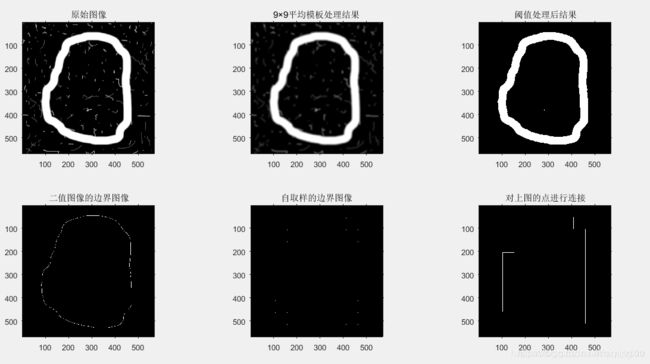
图(a)显示了一幅 570x570 大小的在镜面反射噪声中嵌入的圆形斧子图像f，这个例子的目的是获得物体外边界的链码和一阶差分。观察图 (a)，很明显，依附在物体上的噪声将导致一条很不规则的边界，它不是物体一般形状的真实描述。 当对噪声边界进行处理时，平滑通常是最常见的处理方式。图 (b)显示了使用 9x9平均模板的处理结果 ，图 ©所示的二值图像是经阈值处理后获得的，使用大约等于图像宽度 10%的网格进行分离。结果点可以显示为一幅图像，如图(e)所示。或使之成为连接序列(见图(f)),与图 (d)相反，通过比较两幅图，为链码采用这种表示方案的优点是很明显的。链码可以从标定过的序列 su 获得。

2，使用最小周长多边形（MPP）的多边形近似

数字边界能够用多边形以任意精度近似，对于闭合曲线，当多边形的顶点数目与边界点数目相同，并且每个顶点与边界点一致时，近似是精确的。
基础知识
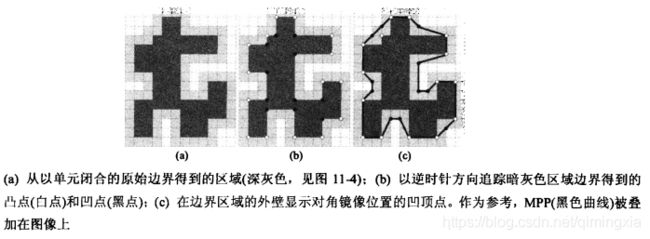
产生计算MPP的算法的一种直观的方法是使用下图b中的一组连接单元来包围a中的一条边界。边界收缩至最小周长的多边形。单元的大小决定多边形近似的精度。

将形状显示为暗黑色如下图。观察下图，内壁的凸点（白点）或外壁的凹点（黑点）对应MPP的顶点。MPP的顶点不是与内墙的凸顶点一致，就是与外墙的凹顶点的镜像顶点一致。只有内墙的凸顶点和外墙的凹顶点才能成为MPP的顶点。MPP算法只需要关注这些顶点。

MPP算法;
获取细胞联合体；Q = qtdecomp(B,threshold,[mindim maxdim])
获取细胞联合体的内部区域；
使用boundaries以4连接顺时针坐标序列的形式获得第2步骤的边界区域；
使用函数fchcode获得该4连接序列的佛雷曼码；
从链码中获得凸点（黑点）和凹点（白点）；
使用黑点作为顶点构造一个初始多边形，在进一步的分析中删除位于该多边形之外的任何白点；
用剩余的黑白点作为顶点构造一个多边形；
删除所有的凹点的黑点；

实现MPP算法的一些M函数
获得包围边界的细胞组合体的第一步是使用函数qtdecomp。区域B由1组成，背景由0组成。

Q = qtdecomp(B, threshold, [mindim maxdim])

其中，Q是包含四叉树结构的稀疏矩阵。如果Q(k,m)非零，那么(k,m)为分解块的左上角，块的大小是Q(k,m)。
函数 qtgetblk： 获得四叉树分解中块的值

[vals, r, c] = qtgetblk(B, Q, mindim)

其中，vals是在B的四叉树分解中包含mindim×maxdim块值的数组，而Q是由函数qtdecomp返回的稀疏矩阵。参数r和c是包含块的左上角行和列坐标的向量。
函数inpolygon:

IN = inpolygon(X, Y, xv, yv)

其中，X 和 Y 是包含待测点的x 和y 坐标的向量，xv 和yv是包含按顺时针和逆时针顺序安排的多边形顶点的x 和y 坐标的向量

函数im2minperpoly :
其中，f是一幅包含单一区域或边界的二值输入图像，cellsize 是细胞联合体中用于形成边界的方形单元的大小。列向量 X 和 Y 包含 MPP 顶点的 x 和 y 坐标。输出 R 是由细胞组 合体包围的区域的二值图像。

3，骨骼
表示一个平面区域结构形状的重要方法是把 它削减成图形。这种削减可以通过细化（也称为抽骨架）算法，获取区域的骨架来实现 。Blum的中轴变换方法（MAT）：设:R是一个区域，B为R的边界点，对于R中 的点p，找p在B上“近”的邻居。如果p有多于一个的邻居，称它属于R的中轴（骨架）。
函数bwmorph用于产生二值图像B中所有区域的骨骼

f = imread('C:\Fig1113(a).tif');
subplot(231),imshow(f),title('原始的图像');
f=im2double(f);   %不是二值图像
h = fspecial('gaussian',25,15);     %加入高斯噪声
g = imfilter(f,h,'replicate');          %用高斯空域模板平滑后的图像
subplot(232),imshow(g),title('用高斯空域模板平滑后的图像');
g = im2bw(g,1.5*graythresh(g));    %对平滑后图像进行阈值处理
subplot(233),imshow(g),title('平滑后图像进行阈值处理');
s = bwmorph(g,'skel',Inf);   
subplot(234),imshow(s),title('骨骼处理后得到的图像');
s1 = bwmorph(s,'spur',8);
subplot(235),imshow(s1),title('刺状突起去除8次后骨骼化得到的图像');
s2 = bwmorph(s,'spur',7);
subplot(236),imshow(s2),title('刺状突起去除7次后骨骼化得到的图像');

处理的第一步是将染色体从与细节无关的背景中分离出来。一种方法是对图像进行平滑，然后进行阈值处理。图 (b)显示了对图像 f 使用 25x25、sig=5 的高斯空域模板进 行平滑后的结果。
接下来，对平滑后的图像进行阈值处理，其中，自动确定阈值，将 graythresh (g) 乘以 1.5 以增加 50%的阈值处理总量。原因在 于，增加阈值将增加从边界中去除的数据数量，因而可以进一步减少噪声。

三，边界描绘子

1，一些简单的描绘子

边界的长度是其最简单的描绘子之一。4连接边界长度被定义为边界像素的数目减1；8连接则是以1计算垂直和水平过渡长度，以根号二计算对角过渡长度。
函数bwperim用于提取包含在图像f中的物体的边界：

g = bwperim(f,conn)

函数diameter用于计算边界的直径、长轴、短轴和边界或区域的基本矩形：

s = diameter(L)

其中，L是标记矩阵，s是具有下面字段的结构：
s.Diameter ：标量，边界或区域中任意两个像素之间的最大距离。
s.MajorAxis：22矩阵，其中的行包含边界或区域的长轴端点的行列坐标。
s.MimorAxis：22矩阵，其中的行包含边界或区域的短轴端点的行列坐标。

2，傅里叶描绘子

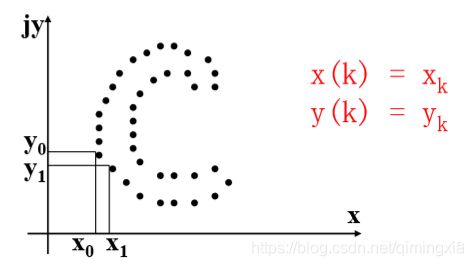
对于XY平面上的每个边界点，将其坐标用复数 表示为：s(k) = x(k) + jy(k)，k=0,1,…,N-1
进行离散傅里叶变换


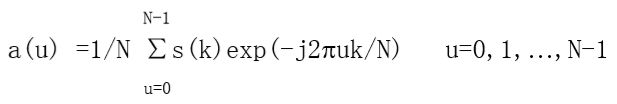
系数a(u)被称为边界的傅里叶描述子。这些系数的傅里叶反变换可以重建S(K)。

随着P的减少，边界细节的丢失就会增加。
傅里叶描绘子

f = imread('C:\Fig1113(a).tif');
subplot(331),imshow(f),title('原始图像');
f=im2double(f);
h=fspecial('gaussian',15,9);
g=imfilter(f,h,'replicate');
g=im2bw(g,0.7);    %变成二值图像
subplot(332),imshow(g),title('阈值处理后');
b=boundaries(g);
b=b{1};
bim=bound2im(b,688,540);    %688×540是图像的尺寸
subplot(333),imshow(bim),title('提取的边界图');
z=frdescp(b);%对边界坐标b进行傅里叶变换系数(有多少个点就有多少个系数)，将b的坐标点看成是复平面中的某个复数
z546=ifrdescp(z,546);%用50%的描述子进行逆变换
z546im=bound2im(z546,688,540);
subplot(334),imshow(z546im),title('546个描述子恢复后');
z110=ifrdescp(z,110);%用10%的描述子进行逆变换
z110im=bound2im(z110,688,540);
subplot(335),imshow(z110im),title('110个描述子恢复后'); 
z56=ifrdescp(z,56);%用5%的描述子进行逆变换
z56im=bound2im(z56,688,540);
subplot(336),imshow(z56im),title('56个描述子恢复后');
z28=ifrdescp(z,28);%用2.5%的描述子进行逆变换
z28im=bound2im(z28,688,540);
subplot(337),imshow(z28im),title('28个描述子恢复后');
z14=ifrdescp(z,14);%用1.25%的描述子进行逆变换
z14im=bound2im(z14,688,540);
subplot(338),imshow(z14im),title('14个描述子恢复后');
z8=ifrdescp(z,8);%用0.70%的描述子进行逆变换
z8im=bound2im(z8,688,540);
subplot(339),imshow(z8im),title('8个描述子恢复后');

描绘子应该尽可能对平移，旋转和尺寸变化不敏感。此时，结果将取决于被处理的顺序，故另一个约束条件是对描绘子对起点应不敏感。傅里叶描绘子并非直接对这些几何变化不敏感，但是这些参数的变化可能与描绘子的简单变换是相关的。

3，统计矩

一维边界表示的形状可通过使用统计矩来定量描述。

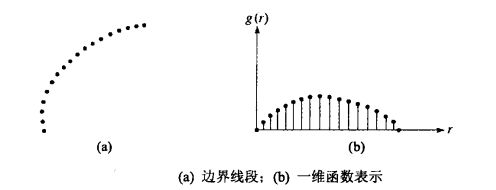
图a中显示了一条边界线段，图b中显示了一个任意变量r的一维函数描述的线段。
当g( r )是上面描绘的一维函数线段时，r是随机变量，则矩为：

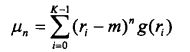
其中
为均值，K是边界上的点数，结果与g的形状有关。
已经完成的工作是把描述任务降到一维函数，与其他技术相比，矩方法的优点是矩的实现非常简单，且矩携带了边界形状的‘物理’解释。

四，使用主分量进行描述

主分量描述适用于边界和区域。用在区域（图像）上可以抽取方差最大的分量（主分量），用在边界上可以对其做缩放、平移和旋转的归一化。主分量（PCA）一般用于数据降维，因为大特征值对应图像细节（高频）。
对于任意给定的坐标对(i,j)，都有n个像素，每一幅图像在那个位置上都有一个像素。这些像素以列向量的形式排列

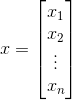
若这些图像的尺寸是M×N，那么在这n幅图像中，包含所有像素的N维向量总共有MN个。

主分量变换（也称为霍特林变换），公式为：

矩阵A的行是归一化为单位长度的Cx的特征向量。
使用主分量

f1 = imread('D:\Fig1130(a).tif');
f2 = imread('D:\Fig1130(b).tif');
f3 = imread('D:\Fig1130(c).tif');
f4 = imread('D:\Fig1130(d).tif');
f5 = imread('D:\Fig1130(e).tif');
f6 = imread('D:\Fig1130(f).tif');
subplot(2,3,1);imshow(f1,[ ]);title('(a可见蓝光波段');
subplot(2,3,2);imshow(f2,[ ]);title('(b)可见绿光波段');
subplot(2,3,3);imshow(f3,[ ]);title('(c)可见红光波段');
subplot(2,3,4);imshow(f4,[ ]);title('(d)近红外波段');
subplot(2,3,5);imshow(f5,[ ]);title('(e)中红外波段');
subplot(2,3,6);imshow(f6,[ ]);title('(f)热红外波段');

f1 = imread('D:\Fig1130(a).tif');
f2 = imread('D:\Fig1130(b).tif');
f3 = imread('D:\Fig1130(c).tif');
f4 = imread('D:\Fig1130(d).tif');
f5 = imread('D:\Fig1130(e).tif');
f6 = imread('D:\Fig1130(f).tif');
s=cat(3,f1,f2,f3,f4,f5,f6);
[ X , R ] = imstack2vectors(s);
P = principalcomps(X, 6);
gl = P.Y(:, 1);
gl = reshape(gl, 512, 512); 
g2 = P.Y(:, 2);
g2 = reshape(g2, 512, 512); 
g3 = P.Y(:, 3);
g3 = reshape(g3, 512, 512); 
g4 = P.Y(:, 4);
g4 = reshape(g4, 512, 512); 
g5 = P.Y(:, 5);
g5 = reshape(g5, 512, 512); 
g6 = P.Y(:, 6);
g6 = reshape(g6, 512, 512); 
subplot(2,3,1);imshow(gl,[ ]);title('(a可见蓝光波段主分量图像');
subplot(2,3,2);imshow(g2,[ ]);title('(b)可见绿光波段主分量图像');
subplot(2,3,3);imshow(g3,[ ]);title('(c)可见红光波段主分量图像');
subplot(2,3,4);imshow(g4,[ ]);title('(d)近红外波段主分量图像');
subplot(2,3,5);imshow(g5,[ ]);title('(e)中红外波段主分量图像');
subplot(2,3,6);imshow(g6,[ ]);title('(f)热红外波段主分量图像');

6幅图像显示计算的住分量图像。最明显的特征是对比度细节的主要部分包含于前两幅图像，且这两幅图像之后的几幅图像的对比度迅速下降。观察特征值发现，前两幅图像的特征值与其他图像相比，大得多。因为特征值是向量Y的元素方差，而该方差是对比度的测度，所以可以预见特征值大的图像对比度高。