机器学习深度学习基础笔记(1)——基础理论
- 该系列是笔者在机器学习深度学习系列课程学习过程中记录的笔记,简单粗暴,仅供参考。
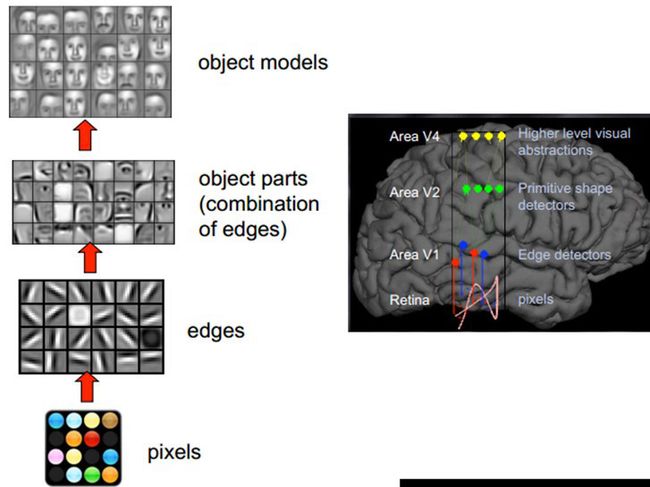
1人脑识别图像过程简介
图片左侧从下往上看,
- 第一层的神经元们接收像素级的信号,
- 第二层从这些输入信息得到一些边缘信息,
- 第三层得到一些简单的原始形状信息,
- 第四层得到一些高层的更具体的形象。
2神经元
- 上图为一个简单的神经元的例子,它经过对三个输入的处理得出一个输出结果,举一个简单的实例:
eg:今天去不去游泳?
天气冷?……………………(冷=0,不冷=1)
是不是周末?……………..(不是=0,是=1)
有没有朋友一起去?……(没有=0,有=1)
w1=5, w2=3, w3=2,threshold=5
(PS:实际神经网络的模型是很复杂的。)
- 对上述公式作个变形(把threshold挪到公式左边):
向量w和向量x
偏移量b=-threshold
这里神经元相当于与非门
与非门可以模拟任何方程
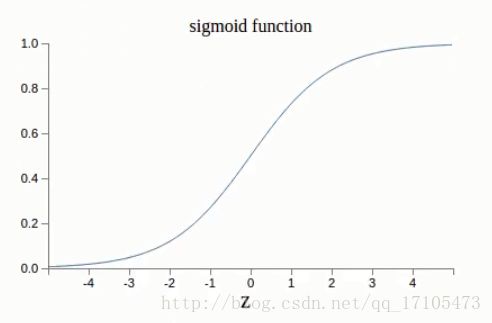
- sigmoid神经元(神经元的一种function)
为了模拟更加细微的变化,使得输入和和输出值从0,1转变为0~1之间的任何的数
![]()
3神经网络基本结构
一个简单的两层神经网络结构:
![]()
多层网络(三层网络):
![]()
Multi Layer perception(MLP):这里实际上是sigmoid neurons,不是perceptions,但是遵循传统,把这一类叫为Multi Layer perception
深度学习的深度主要指隐藏层数量很多
4假设识别手写数字的图片
![]()
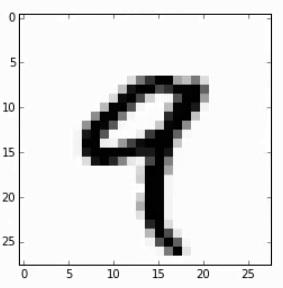
- 取其中一张图:
图片像素是28×28,那么输入层总共要有28×28=784个神经元
如果输出层只有一个神经元,那输出如果>0.5判断其是9,<0.5判断其不是9
Feed Forward Network:前馈型神经网络中没有循环,信息单项向前传递
- 假设用以下神经网络进行识别(两层):
![]()
输入层:28×28=784个神经元——每个神经元代表一个像素的值:0.0——全白,1.0——全黑,中间值为灰度(浅灰~深灰)
一个隐藏层:n个神经元(本例中n=15)
输出层:10个神经元,分别代表对输入的手写数字为0~9这十个数字的可能性
eg:第一个神经元(代表0)的输出值=1,其他的输出都<1,则判断输入的手写数字为0
- 总结:
输入层对应像素点。
隐藏层:从最低的像素级别到最高的概念级别,其中间的隐藏特征通过隐藏层学习得来。
输出层对应分类。
5梯度下降算法
梯度下降(gradient descent)
- 首先介绍一个数据库,它一共有70000张手写数字的黑白图片,名为:
Modified National Institute of Standards and Technology(MNIST dataset)
训练集:60000张图片——用于训练
测试集:10000张图片——用于测试
扫描自250位员工的手写字体
x:训练输入,28×28=784d向量,每个值代表一张灰度图中的一个像素值
y=y(x):10d向量
如果输入的某个图片是数字6
理想输出是y(x)=( 0, 0, 0, 0, 0, 0, 1, 0, 0, 0 )T
(ps:T是转为纵向的意思)
- cost function(又称loss function,objective function)目标函数(又称损失函数)
![]()
C:cost预测值和真实值的差别
w:weight权重
b:bias偏移量
n:训练数据实例个数
x:输入值
y(x):神经网络预测得出的输出值——测出的答案
a:实际应该输出的值(当x是输入时)——正确答案
:向量的length function即
C(w,b)越小越好,输出的预测值和真实值差别越小越好
目标:最小化C(w,b)
- 最小化问题可以用梯度下降解决
C(v):v有两个变量 v1和v2
PS:通常可以用微积分来解决,但如果v包含很多变量,(最大的神经网络具有的成本函数,取决于数十亿的权重和偏差,这非常复杂,仅仅使用微积分最小化是不行的),就无法用微积分解决了,所以用梯度下降解决。
假设把寻找最小的C(v)想象成一个小球从山谷滚下来的过程(梯度下降),小球所在位置就是当前的C(v)的值,小球越靠近最低点,C(v)越小。
- 注意几点:
小球滚落的时候,运气好点会落在最低点,运气不好就可能陷入局部最优。
下降的前提是目标函数要是凸函数convex(就是画出来的图是碗状的)
learning rate 会自动减小
![]()
寻找最小的C(v):
![]()
![]()
![]() :学习率
:学习率
,:求偏导
新的![]() ,
,![]() 就是
就是![]() ,
,![]() 减去各自对应的偏导
减去各自对应的偏导
通过不断的更新参数实现C(v)的最小化
6梯度下降算法的变种-随机梯度下降
![]()
目标函数:
![]()
变化量:
coss function 的 gradient vector:
(![]() :梯度向量C)
:梯度向量C)
由以上3个公式推导出;
![]()
设定:
所以C不断减小
![]()
回顾目标函数:
![]()
是平均的cost
权重和偏移量更新方程;
![]()
![]()
对于每个训练实例x,都要计算梯度向量gradient vector:
如果训练数量集很大,会花费很长时间,学习过程太慢
所以,改进算法得出一个变种,称为:
随机梯度下降算法(stochastic gradient descent):
基本思想:从所有训练实例中取出一个小的采样(sample):X1,X2,….,Xm (mini-batch)来估计,大大提高学习速度
eg:选举调查(随机从所有选民中抽取m个人)
如果样本够大:
代入更新方程;
![]()
![]()
然后重新选则一个mini-batch用来训练,直到用完所有的训练实例,一轮epoch完成