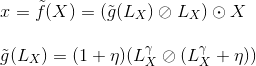论文阅读笔记------iTM-Net: Deep Inverse Tone Mapping Using Novel Loss Function Considering TMO
Kinoshita Y, Kiya H. iTM-Net: Deep Inverse Tone Mapping Using Novel Loss Function Considering Tone Mapping Operator[J]. IEEE Access, 2019, 7: 73555-73563.
摘要：
在本文中，我们提出了一种新的反色调映射网络，称为iTM-Net。在训练iTM-Net时，我们也提出了一个新的损失函数，它考虑了低动态范围(LDR)和高动态范围(HDR)图像之间的非线性关系。针对卷积神经网络的色调逆映射问题，我们首先指出训练具有标准损失函数的CNNs会因为LDR和HDR图像之间的非线性关系而产生问题。针对这一问题，提出了一种基于色调映射算子的HDR图像非线性损失函数映射算法，将HDR图像映射为LDR图像，并计算了色调映射图像与预测图像之间的距离。提出的损失函数不仅可以对HDR图像进行归一化处理，而且可以减少LDR图像与HDR图像之间的非线性关系。实验结果表明，无论是HDR- vdp -2.2还是PU编码的C MS-SSIM，本文提出的iTM-Net预测的HDR图像的质量都比传统的反色调映射方法(包括目前的技术水平)预测的HDR图像的质量都要高。此外，与不考虑非线性关系的损耗函数相比，本文提出的损耗函数可以改善网络的性能。
在本文中，我们提出了一种新的反色调映射网络，称为iTM-Net。与[18]相似，我们的目标是通过线性化的iTM-Net获得相对亮度。为了实现这一点，我们还提出了一个新的损失函数，它考虑了LDR和HDR图像之间的非线性关系。在新的损失函数中，利用一个可逆的色调映射算子将目标HDR图像的色调映射到LDR图像中，然后计算色调映射图像与预测图像之间的距离。提出的损失函数不仅可以对HDR图像进行归一化处理，而且可以广泛分布像LDR图像这样的HDR图像的像素值。我们的iTM-Net是在不使用生成对抗网络的情况下实现的，目的是使iTM-Net适用于具有不同分辨率的图像
所有HDR图像被简单地归一化到[0;1]采用最小-最大归一化。然而，使用归一化的HDR图像来计算预测损失会导致一个问题，即归一化图像的像素值大多分布在一个较窄的范围内。这是由于LDR和HDR图像之间的非线性关系，所以正如[17]中指出的，LDR和HDR图像的图像统计差异很大。因此，我们的目标是提高基于cnn的反向色调映射的性能，通过使用一种新的损失函数来考虑学习HDR图像的非线性关系
在训练中，所有输入的LDR图像x都是使用各种虚拟摄像机 从目标HDR图像E中生成的
loss function:
ExpandNet [18] 中的loss 为：
然而，与LDR图像不同的是，HDR图像的像素值不均匀分布在一个非常宽的[17]范围内，因此min-max归一化不适合学习HDR图像
基于这个原因，本文采用可逆的色调映射操作 
代替 min-max 标准化 
Reinhard’s global operator [31] is utilized as ,
分别表示像素级的乘法和除法，![a \in [0, 1]](http://img.e-com-net.com/image/info8/f677e0ebb3914616acbbafcea471a2fe.gif){kind=small}
, 
表示几何平均数
PREDICTION:
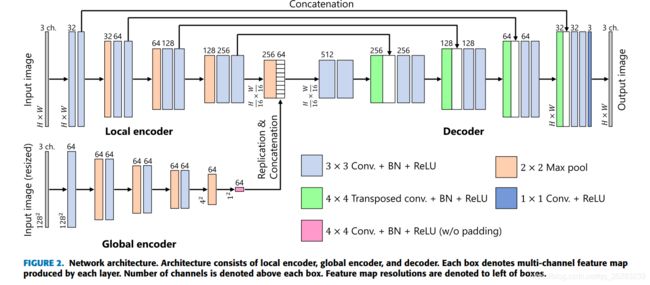
ITM-NET 结构：
网络由三部分构成local encoder + global encoder + decoder：
local encoder: 输入 P = H * W , 24-bit LDR 图像
global encoder: 输入是将输入LDR图像resize到 128*128
3*3 Conv. + BN +ReLU : filter size = 3 * 3, stride=1, padding=1, BN = batch normalization
2 * 2 Max pool: kernel size = 2 * 2, stride =2
4*4 Transposed Conv. + BN + ReLU: filter size=4*4, stride = 1/2, padding=1
1 * 1 Conv. +ReLU : filter size = 1 * 1, stride = 1, padding=1
4 * 4 Conv. + BN + ReLU(w/o padding): filter size = 4 * 4, padding=0
在工作[18]中，Marnerides等人声称U-Net在预测的HDR图像中会导致不必要的块效应。我们的初步实验结果表明，块效应现象是由于其网络结构无法处理全局图像信息造成的。因此，我们利用全局编码器并结合两个编码器提取的特征来防止失真。
实验：
从 HDR图像 ![\Tilde{E} = Resize_{255*255}(Crop_{short side * random[0.2,0.6]}(E))](http://img.e-com-net.com/image/info8/13bc66b3c2134e54afb3403008afc4b2.gif){kind=small}
计算曝光X: 
快门速度 ![\Deltat(v) = 0.18 \cdot 2^v / G(L_{\Tilde{E}}) , v \in [-2, 2]](http://img.e-com-net.com/image/info8/7202812637e344bca73493fa0070d57a.gif){kind=small}
v 是随机数
产生输入LDR图像x :
iTM-Net 训练中 使用Adam 优化， 参数为
对比试验：Direct ITMO[15], pseudo-multi-exposure-based tone fusion(PMET)[13], ExpandNet[18],和以下的
[13] T.-H. Wang, C.-W. Chiu, W.-C. Wu, J.-W. Wang, C.-Y. Lin, C.-T. Chiu, and J.-J. Liou, ‘‘Pseudo-multiple-exposure-based tone fusion with local region adjustment,’’ IEEE Trans. Multimed., vol. 17, no. 4, pp. 470–484, Apr. 2015.
[15] Y. Kinoshita, S. Shiota, and H. Kiya, ‘‘Fast inverse tone mapping based on Reinhard’s global operator with Estimated Parameters,’’ IEICE Trans. Fundam. Electron. Commun. Comput. Sci., vol. 100, no. 11, pp. 2248–2255, Nov. 2017.[18] Marnerides D, Bashford‐Rogers T, Hatchett J, et al. ExpandNet: A deep convolutional neural network for high dynamic range expansion from low dynamic range content[C]//Computer Graphics Forum. 2018, 37(2): 37-49.
[31] E. Reinhard, M. Stark, P. Shirley, and J. Ferwerda, ‘‘Photographic tone reproduction for digital images,’’ ACM Trans. Graph., vol. 21, no. 3, pp. 267–276, Jul. 2002.