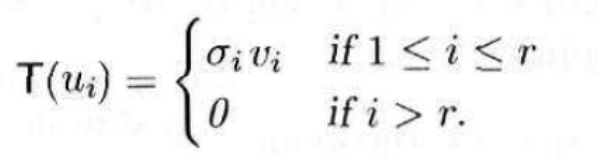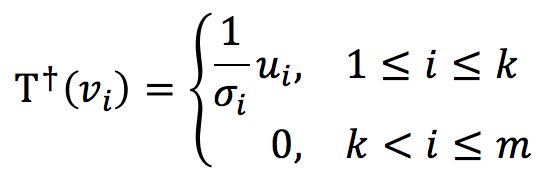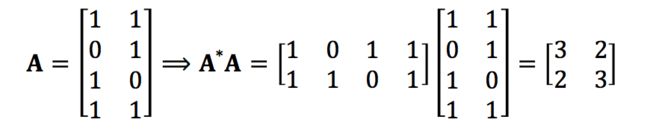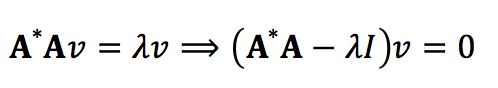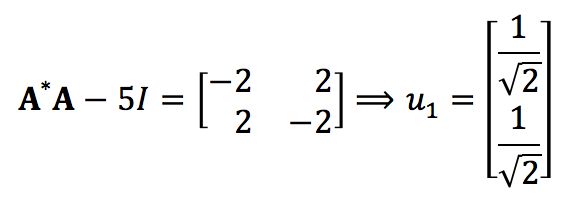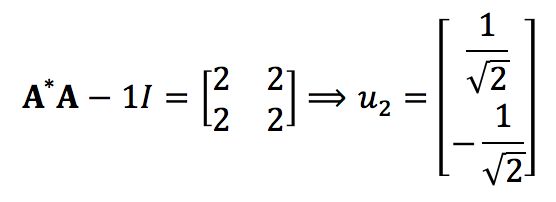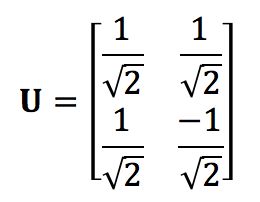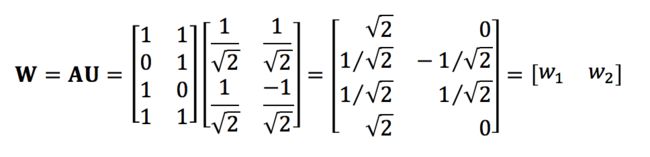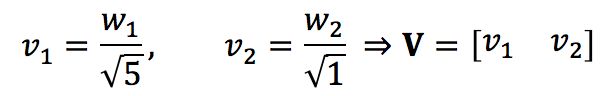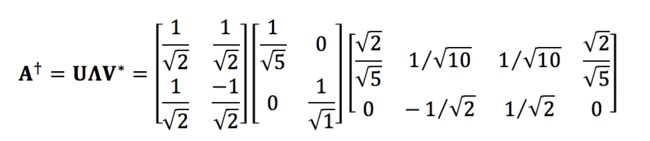（十八）通俗易懂理解——SVD降维（协同过滤）

最近内容看的挺少，但是遇到仍是一大堆不懂的知识点，感觉有很多坑要弥补。这节给自己稍微复习记录一下SVD降维算法，该算法在推荐上有一定的应用。其实挺想吐槽一下网上的一些博客，虽然人家也是给自己做个记录，不过对于本渣渣，实在理解能力有限，细节上的处理仍是不懂，希望今后我的记录不会出现类似问题。

 

线性代数相关知识：

任意一个M*N的矩阵A（M行*N列，M>N），可以被写成三个矩阵的乘积：

1. U：（M行M列的列正交矩阵）

2. S：（M*N的对角线矩阵，矩阵元素非负）

3. V：（N*N的正交矩阵的倒置）

即 A=U*S*V'（注意矩阵V需要倒置）

 

直观地说：

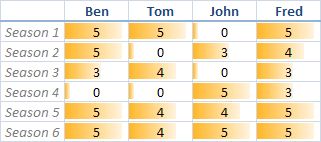
假设我们有一个矩阵，该矩阵每一列代表一个user，每一行代表一个item。

如上图，ben,tom….代表user，season n代表item。

矩阵值代表评分（0代表未评分）：

如 ben对season1评分为5，tom对season1 评分为5，tom对season2未评分。

 

机器学习和信息检索：

机器学习的一个最根本也是最有趣的特性是数据压缩概念的相关性。

如果我们能够从数据中抽取某些有意义的感念，则我们能用更少的比特位来表述这个数据。

从信息论的角度则是数据之间存在相关性，则有可压缩性。

SVD就是用来将一个大的矩阵以降低维数的方式进行有损地压缩。

 

降维：（相对于机器学习中的PCA）

下面我们将用一个具体的例子展示svd的具体过程。

首先是A矩阵。

A = 5 5 0 5 5 0 3 4 3 4 0 3 0 0 5 3 5 4 4 5 5 4 5 5

 

做到这里，我们就需要进行SVD降维了，先上降维的算法原理。

一、伪逆（pseudo-inverse）

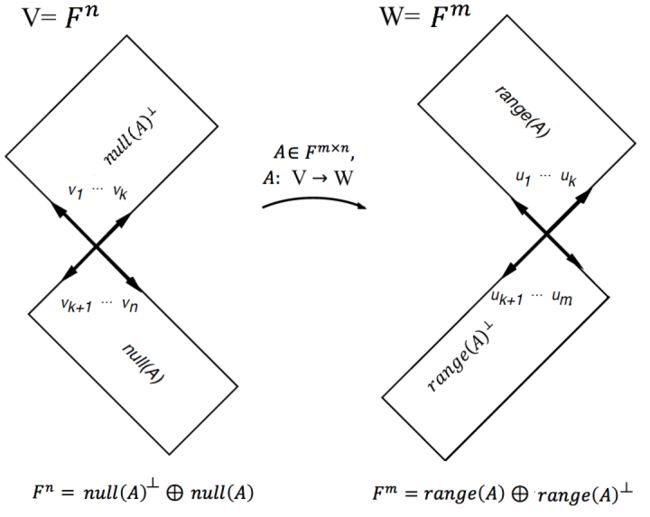
由于奇异矩阵或非方阵的矩阵不存在逆矩阵。但有时我们又希望给这样的矩阵，构造出一个具有类似逆矩阵性质的结果，于是人们便提出了“伪逆”的构想。这个构想的出发点是基于下面这张图，一个变换T（或者一个矩阵A）的值域V可以分解成相互垂直的两个部分，即V = N(A) ⊕ N(A)⊥。一个变换T是可逆的 if and only if T是one-one and onto。而定理2.4告诉我们T是one-one if and only if N(A)={0}。也就是说，如果T是不可逆的，也就代表当我们引入N(A)后会破坏从V到W的一一对应关系。所以很自然的，我们会想到，如果把N(A)从V中剥离，那么剩下的 N(A)⊥到Range(A)就能构成一一对应关系，也就存在逆变换（或逆矩阵）。

我们建立了一个可逆的变换T:N(T)⊥→Range(T)，令L=TN(T)⊥，这样L就有逆变换了。基于这样的考量，我们就有了下面这个pseudoinverse的定义。

二、利用SVD计算伪逆

我们要求T的伪逆，就要设法求得N(A)、N(A)⊥、Range(A)和Range(A)⊥。而借由SVD，这些子空间都非常容易得到（这里注意参考http://blog.csdn.net/baimafujinji/article/details/6474273）：

（1）Span{uk+1, ..., un}=N(A)

（2）Span{u1, ..., uk}=N(A)⊥

（3）Range(A) = Span{v1, ..., vk}

（4）Range(A)⊥=Span{vk+1, ..., vm}

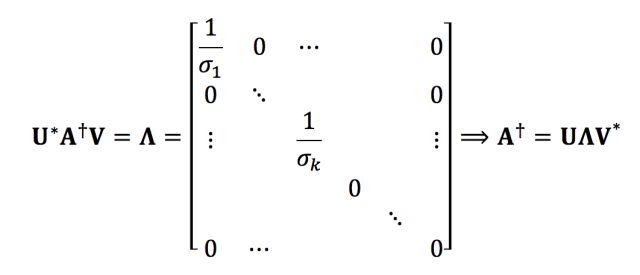
注意在SVD的算子版本中，我们给出的分解形式是

再根据上面伪逆的定义可得(k=r)：

而上面这个式子又是一个SVD，（A的SVD是V*AU=∑）所以有

 

以上是一个理论，但是理论上的还不如直接来个实际例子说明。

三、一个具体的例子

我们来具体算一个矩阵A的伪逆：

易知，rank(A*A)=2。下面来求矩阵A*A的特征值，于是有

接下来求对应的特征向量，因为

所以可知当λ1=5时，对应的特征向量（注意结果要正交归一化）：

同理还有当λ2=1时，对应的特征向量

如此便得到了SVD中需要的U矩阵

为了求出矩阵V，先求W：

于是可知

所以根据公式A的伪逆就是

 

这就是整个求解过程。

回到我们一开始的位置，求出A的分解形式矩阵。

U = -0.4472 -0.5373 -0.0064 -0.5037 -0.3857 -0.3298 -0.3586 0.2461 0.8622 -0.1458 0.0780 0.2002 -0.2925 -0.4033 -0.2275 -0.1038 0.4360 0.7065 -0.2078 0.6700 -0.3951 -0.5888 0.0260 0.0667 -0.5099 0.0597 -0.1097 0.2869 0.5946 -0.5371 -0.5316 0.1887 -0.1914 0.5341 -0.5485 0.2429 S = 17.7139 0 0 0 0 6.3917 0 0 0 0 3.0980 0 0 0 0 1.3290 0 0 0 0 0 0 0 0 Vtranspose = -0.5710 -0.2228 0.6749 0.4109 -0.4275 -0.5172 -0.6929 0.2637 -0.3846 0.8246 -0.2532 0.3286 -0.5859 0.0532 0.0140 -0.8085

分解矩阵之后我们首先需要明白S的意义。

可以看到S很特别，是个对角线矩阵。

每个元素非负，而且依次减小，从几何意义上来说，此值和特征向量中的特征值的权重有关。

所以可以取S对角线上前k个元素。

当k=2时候即将S(6*4)降维成S(2*2)，

同时U(6*6),Vtranspose(4*4)相应地变为 U(6*2),Vtranspose(4*2).

如下图（图片里的usv矩阵元素值和我自己matlab算出的usv矩阵元素值有些正负不一致，但是本质是相同的）：

此时我们用降维后的U，S，V来相乘得到A2

A2=U(1:6,1:2)*S(1:2,1:2)*(V(1:4,1:2))' //matlab语句 A2 = 5.2885 5.1627 0.2149 4.4591 3.2768 1.9021 3.7400 3.8058 3.5324 3.5479 -0.1332 2.8984 1.1475 -0.6417 4.9472 2.3846 5.0727 3.6640 3.7887 5.3130 5.1086 3.4019 4.6166 5.5822

此时我们可以很直观地看出，A2和A很接近，这就是之前说的降维可以看成一种数据的有损压缩。

 

接下来我们开始分析该矩阵中数据的相关性

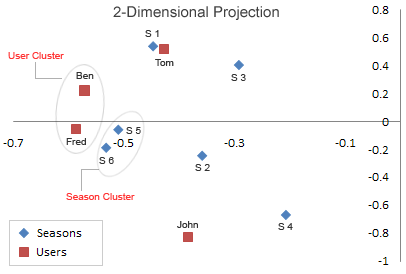
我们将u的第一列当成x值，第二列当成y值（即u的每一行用一个二维向量表示）

同理，v的每一行也用一个二维向量表示。

如下图：

从图中可以看出:

Season5，Season6特别靠近。Ben和Fred也特别靠近。

同时我们仔细看一下A矩阵可以发现，A矩阵的第5行向量和第6行向量特别相似，Ben所在的列向量和Fred所在的列向量也特别相似。

 

所以，从直观上我们发现，U矩阵和V矩阵可以近似来代表A矩阵，换据话说就是将A矩阵压缩成U矩阵和V矩阵，至于压缩比例得看当时对S矩阵取前k个数的k值是多少。

 

到这里，我们已经完成了一半。

 

寻找相似用户

我们假设，现在有个名字叫Bob的新用户，并且已知这个用户对season n的评分向量为：[5 5 0 0 0 5]。（此向量为行向量）

我们的任务是要对他做出个性化的推荐。

我们的思路首先是利用新用户的评分向量找出该用户的相似用户。

对图中公式不做证明，只需要知道结论：得到一个Bob的二维向量，即知道Bob的坐标。（本质上是特征的降维转换）

 

将Bob坐标添加进原来的图中：

然后从图中找出和Bob最相似的用户。

 

注意，最相似并不是距离最近的用户，这里的相似用余弦相似度计算，即夹角与Bob最小的用户坐标，可以计算出最相似的用户是ben。

 

接下来的推荐策略就完全取决于个人选择了。

 

这里介绍一个非常简单的推荐策略：

找出最相似的用户，即ben。

观察ben的评分向量为：【5 5 3 0 5 5】。

对比Bob的评分向量：【5 5 0 0 0 5】。

然后找出ben评分过而Bob未评分的item并排序，即【season 5：5，season 3：3】。

即推荐给Bob的item依次为 season5 和 season3。

 

最后还有一些关于整个推荐思路的可改进的地方：

1.svd本身就是时间复杂度高的计算过程，如果数据量大的情况恐怕时间消耗无法忍受。不过可以使用梯度下降等机器学习的相关方法来进行近似计算，以减少时间消耗。

2.相似度计算方法的选择，有多种相似度计算方法，每种都有对应优缺点，对针对不同场景使用最适合的相似度计算方法。

3.推荐策略：首先是相似用户可以多个，每个由相似度作为权重来共同影响推荐的item的评分。

 

 

参考网址：https://blog.csdn.net/baimafujinji/article/details/6472735

参考网址：https://yanyiwu.com/work/2012/09/10/SVD-application-in-recsys.html