Machine Learning 学习笔记(九)——决策树

决策树实战

说在前面

• 本文参考了 https://blog.csdn.net/jiaoyangwm/article/details/79525237这篇博客，这篇博客写的很好，值得推荐，就是里面有一个错误是列表拷贝的问题，要用到深拷贝。否则会使属性列表清空计算的信息增益为0。
• 其次参考了西瓜书中的叙述，这里决策树的信息增益其实和信息论相联系。
• 本篇文章是从jupyter notebook 中直接导出的，后面添加了图片，格式稍微有点不美观。

1.决策树（decision tree）

• 是一种基本的分类与回归方法，此处主要讨论分类的决策树。在分类问题中，表示基于特征对实例进行分类的过程，可以认为是if-then的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。
• 决策树通常有三个步骤：特征选择、决策树的生成、决策树的修剪。
• 用决策树分类：从根节点开始，对实例的某一特征进行测试，根据测试结果将实例分配到其子节点，此时每个子节点对应着该特征的一个取值，如此递归的对实例进行测试并分配，直到到达叶节点，最后将实例分到叶节点的类中。

2.决策树的构建

• 决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。

（1） 开始：构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。

（2） 如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。

（3）如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。

（4）每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树。

信息增益

• 划分数据集的大原则是：将无序数据变得更加有序，但是各种方法都有各自的优缺点，信息论是量化处理信息的分支科学，在划分数据集前后信息发生的变化称为信息增益，获得信息增益最高的特征就是最好的选择，所以必须先学习如何计算信息增益，集合信息的度量方式称为香农熵，或者简称熵。
• 熵定义为信息的期望值，如果待分类的事物可能划分在多个类之中，则符号$x_i$的信息定义为：
  $$I(x_i)=-lo{g}_{2}p(x_i)$$
  为了计算熵，我们需要计算所有类别所有可能值所包含的信息期望值，通过下式得到：
  $$H=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)$$
  其中，n为分类数目，熵越大，随机变量的不确定性就越大。
• 当熵中的概率由数据估计(特别是最大似然估计)得到时，所对应的熵称为经验熵(empirical entropy)。什么叫由数据估计？比如有10个数据，一共有两个类别，A类和B类。其中有7个数据属于A类，则该A类的概率即为十分之七。其中有3个数据属于B类，则该B类的概率即为十分之三。浅显的解释就是，这概率是我们根据数据数出来的。我们定义样本数据表中的数据为训练数据集D，则训练数据集D的经验熵为H(D)，|D|表示其样本容量，及样本个数。设有K个类Ck，k = 1,2,3,···,K，|Ck|为属于类Ck的样本个数，这经验熵公式可以写为：
  $$H(D)=-\sum \frac{|c_k|}{D}lo{g}_2\frac{c_k}{D}$$
• 在理解信息增益之前，要明确——条件熵
  信息增益表示得知特征X的信息而使得类Y的信息不确定性减少的程度。
  条件熵H(Y∣X)H(Y∣X)表示在已知随机变量X的条件下随机变量Y的不确定性，随机变量X给定的条件下随机变量Y的条件熵(conditional entropy) H(Y|X)，定义X给定条件下Y的条件概率分布的熵对X的数学期望：
  $$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$
• 信息增益：信息增益是相对于特征而言的。所以，特征A对训练数据集D的信息增益Gain(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：
  $$Gain(D,A)=H(D)-H(D|A)$$
  一般地，熵H(D)与条件熵H(D|A)之差成为互信息(mutual information)。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
• 信息增益比(增益率)：特征A对训练数据集D的信息增益比Gain_ratio定义为其信息增益Gain(D,A)与训练数据集D的经验熵之比：
  $$Gain\_ratio=\frac{Gain(D,A)}{H(D)}$$

3.计算经验熵(信息熵)

from math import log
def creatDataSet():
    # 数据集
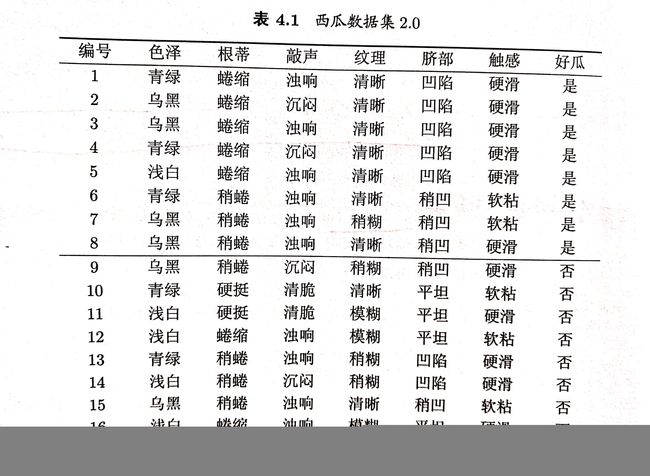
    dataSet=[['青绿','蜷缩','浊响','清晰','凹陷','硬滑','是'],
             ['乌黑','蜷缩','沉闷','清晰','凹陷','硬滑','是'],
             ['乌黑','蜷缩','浊响','清晰','凹陷','硬滑','是'],
             ['青绿','蜷缩','沉闷','清晰','凹陷','硬滑','是'],
             ['浅白','蜷缩','浊响','清晰','凹陷','硬滑','是'],
             ['青绿','稍蜷','浊响','清晰','稍凹','软粘','是'],
             ['乌黑','稍蜷','浊响','稍糊','稍凹','软粘','是'],
             ['乌黑','稍蜷','浊响','清晰','稍凹','硬滑','是'],
             ['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑','否'],
             ['青绿','硬挺','清脆','清晰','平坦','软粘','否'],
             ['浅白','硬挺','清脆','模糊','平坦','硬滑','否'],
             ['浅白','蜷缩','浊响','模糊','平坦','软粘','否'],
             ['青绿','稍蜷','浊响','稍糊','凹陷','硬滑','否'],
             ['浅白','稍蜷','沉闷','稍糊','凹陷','硬滑','否'],
             ['乌黑','稍蜷','浊响','清晰','稍凹','软粘','否'],
             ['浅白','蜷缩','浊响','模糊','平坦','硬滑','否'],
             ['青绿','蜷缩','沉闷','稍糊','稍凹','硬滑','否']]
    # 分类属性
    labels = ['色泽','根蒂','敲声','纹理','脐部','触感']
    return dataSet, labels
dataSet, labels = creatDataSet()

def calculate_Ent(dataSet):
    # 返回数据集行数
    n = len(dataSet)
    label_counts = {}
    # 对每组特征向量进行统计
    for feat in dataSet:
        current_label = feat[-1]    # 提取标签信息
        if current_label not in label_counts.keys():
            label_counts[current_label] = 0
        label_counts[current_label] += 1
    Ent = 0.0
    # 计算经验熵
    print(label_counts)
    for key in label_counts:
        prob = float(label_counts[key]/n)    # 该标签的概率p
        Ent -= prob * log(prob,2)
    return Ent
Ent = calculate_Ent(dataSet)
Ent

{'是': 8, '否': 9}

0.9975025463691153

4.计算信息增益

def split_dataSet(dataSet,axis,value):
    ret_dataSet = []
    for feat in dataSet:
        if feat[axis] == value:
            reduce_feat = feat[:axis]
            reduce_feat.extend(feat[axis+1:])
            ret_dataSet.append(reduce_feat)
    return ret_dataSet

def choose_beat_feature(dataSet):
    # 特征数量
    num_feat = len(dataSet[0]) - 1
    # 计算数据集的信息熵
    Ent = calculate_Ent(dataSet)
    # 最佳信息增益
    best_gain = 0.0
    # 最佳信息增益索引值
    best_feat = -1
    # 遍历所有特征
    for i in range(num_feat):
        # 获取dataSet的第i个属性
        feat_list = [example[i] for example in dataSet]
        # 创建set集合，元素不可重复
        feats = set(feat_list)
        # 信息条件熵
        Ent_condition = 0.0
        # 计算条件熵
        for value in feats:
            # 划分后的子集
            sub_dataSet = split_dataSet(dataSet,i,value)
            # 计算子集的概率 (|Dv|/|D|)
            prob = len(sub_dataSet)/float(len(dataSet))
            # 根据公式求条件熵
            Ent_condition += prob * calculate_Ent(sub_dataSet)
        # 求出信息增益
        gain = Ent - Ent_condition
        print("\"%s\"属性的信息增益为%.3f" %(labels[i],gain))
        if gain > best_gain:
            best_gain = gain
            best_feat = i
    return best_feat
best_feat = choose_beat_feature(dataSet)
print("最优属性索引值为："+labels[best_feat])

{'是': 8, '否': 9}
{'是': 3, '否': 3}
{'是': 1, '否': 4}
{'是': 4, '否': 2}
"色泽"属性的信息增益为0.108
{'是': 3, '否': 4}
{'否': 2}
{'是': 5, '否': 3}
"根蒂"属性的信息增益为0.143
{'是': 6, '否': 4}
{'否': 2}
{'是': 2, '否': 3}
"敲声"属性的信息增益为0.141
{'否': 3}
{'是': 7, '否': 2}
{'是': 1, '否': 4}
"纹理"属性的信息增益为0.381
{'是': 5, '否': 2}
{'是': 3, '否': 3}
{'否': 4}
"脐部"属性的信息增益为0.289
{'是': 6, '否': 6}
{'是': 2, '否': 3}
"触感"属性的信息增益为0.006
最优属性索引值为：纹理

5.用ID3算法构建决策树

• ID3算法的核心是在决策树各个结点上对应信息增益准则选择特征，递归地构建决策树。
  具体方法是：

（1）从根结点(root node)开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征。

（2）由该特征的不同取值建立子节点，再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止；

（3）最后得到一个决策树。

import operator
import copy
def major_cnt(class_list):
    class_count = {}
    # 统计每个类别中元素出现的次数
    for vote in class_list:
        if vote not in class_count.keys():
            class_count[vote] = 0
        class_count[vote] += 1
    sorted_class_cnt = sorted(class_count.items(),key=operator.itemgetter(1),reverse=True)
    return sorted_class_cnt[0][0]

def creat_tree(dataSet, labels, feat_labels):
    # 取分类标签
    class_list = [example[-1] for example in dataSet]
    # 如果类别完全相同，则停止继续分类
    if class_list.count(class_list[0]) == len(class_list):
        return class_list[0]
    # 遍历完所有特征时返回出现次数最多的类标签
    if len(dataSet[0]) == 1:
        return major_cnt(class_list)
    # 选择最优特征
    best_feat = choose_beat_feature(dataSet)
    # 最优特征的标签
    best_feat_label = labels[best_feat]
    feat_labels.append(best_feat_label)
    # 根据最优特征生成树
    mytree = {best_feat_label:{}}
    # 删除已经使用的特征标签
    del(labels[best_feat])
    # 得到训练集中所有最优特征的属性值
    feat_values = [example[best_feat] for example in dataSet]
    # 去掉重复的属性值
    feat = set(feat_values)
    # 遍历特征，创建决策树
    for value in feat:
        labels2 = copy.deepcopy(labels)
        print("现在进行的是%s 下面的\"%s\"类" % (best_feat_label,value))
        mytree[best_feat_label][value] = creat_tree(split_dataSet(dataSet,best_feat,value),labels2,feat_labels)
    return mytree
feat_labels=[]
dataSet,labels = creatDataSet() 
mytree = creat_tree(dataSet,labels,feat_labels)
print(mytree)

{'是': 8, '否': 9}
{'是': 3, '否': 3}
{'是': 1, '否': 4}
{'是': 4, '否': 2}
"色泽"属性的信息增益为0.108
{'是': 3, '否': 4}
{'否': 2}
{'是': 5, '否': 3}
"根蒂"属性的信息增益为0.143
{'是': 6, '否': 4}
{'否': 2}
{'是': 2, '否': 3}
"敲声"属性的信息增益为0.141
{'否': 3}
{'是': 7, '否': 2}
{'是': 1, '否': 4}
"纹理"属性的信息增益为0.381
{'是': 5, '否': 2}
{'是': 3, '否': 3}
{'否': 4}
"脐部"属性的信息增益为0.289
{'是': 6, '否': 6}
{'是': 2, '否': 3}
"触感"属性的信息增益为0.006
现在进行的是纹理 下面的"模糊"类
现在进行的是纹理 下面的"清晰"类
{'是': 7, '否': 2}
{'是': 3, '否': 1}
{'是': 1}
{'是': 3, '否': 1}
"色泽"属性的信息增益为0.043
{'是': 2, '否': 1}
{'否': 1}
{'是': 5}
"根蒂"属性的信息增益为0.458
{'是': 5, '否': 1}
{'否': 1}
{'是': 2}
"敲声"属性的信息增益为0.331
{'是': 5}
{'是': 2, '否': 1}
{'否': 1}
"脐部"属性的信息增益为0.458
{'是': 6}
{'是': 1, '否': 2}
"触感"属性的信息增益为0.458
现在进行的是根蒂 下面的"稍蜷"类
{'是': 2, '否': 1}
{'是': 1}
{'是': 1, '否': 1}
"色泽"属性的信息增益为0.252
{'是': 2, '否': 1}
"根蒂"属性的信息增益为0.000
{'是': 2, '否': 1}
"敲声"属性的信息增益为0.000
{'是': 1}
{'是': 1, '否': 1}
"脐部"属性的信息增益为0.252
现在进行的是色泽 下面的"青绿"类
现在进行的是色泽 下面的"乌黑"类
{'是': 1, '否': 1}
{'是': 1, '否': 1}
"色泽"属性的信息增益为0.000
{'是': 1, '否': 1}
"根蒂"属性的信息增益为0.000
{'是': 1}
{'否': 1}
"敲声"属性的信息增益为1.000
现在进行的是触感 下面的"硬滑"类
现在进行的是触感 下面的"软粘"类
现在进行的是根蒂 下面的"硬挺"类
现在进行的是根蒂 下面的"蜷缩"类
现在进行的是纹理 下面的"稍糊"类
{'是': 1, '否': 4}
{'是': 1, '否': 1}
{'否': 1}
{'否': 2}
"色泽"属性的信息增益为0.322
{'是': 1, '否': 3}
{'否': 1}
"根蒂"属性的信息增益为0.073
{'是': 1, '否': 1}
{'否': 3}
"敲声"属性的信息增益为0.322
{'否': 2}
{'是': 1, '否': 2}
"脐部"属性的信息增益为0.171
{'否': 4}
{'是': 1}
"触感"属性的信息增益为0.722
现在进行的是触感 下面的"硬滑"类
现在进行的是触感 下面的"软粘"类
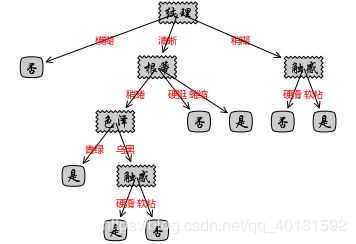
{'纹理': {'模糊': '否', '清晰': {'根蒂': {'稍蜷': {'色泽': {'青绿': '是', '乌黑': {'触感': {'硬滑': '是', '软粘': '否'}}}}, '硬挺': '否', '蜷缩': '是'}}, '稍糊': {'触感': {'硬滑': '否', '软粘': '是'}}}}

6.绘制决策树

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# 获取树的叶子节点数目
def get_num_leafs(decision_tree):
    num_leafs = 0
    first_str = next(iter(decision_tree))
    second_dict = decision_tree[first_str]
    for k in second_dict.keys():
        if isinstance(second_dict[k], dict):
            num_leafs += get_num_leafs(second_dict[k])
        else:
            num_leafs += 1
    return num_leafs

# 获取树的深度
def get_tree_depth(decision_tree):
    max_depth = 0
    first_str = next(iter(decision_tree))
    second_dict = decision_tree[first_str]
    for k in second_dict.keys():
        if isinstance(second_dict[k], dict):
            this_depth = 1 + get_tree_depth(second_dict[k])
        else:
            this_depth = 1
        if this_depth > max_depth:
            max_depth = this_depth
    return max_depth

# 绘制节点
def plot_node(node_txt, center_pt, parent_pt, node_type):
    arrow_args = dict(arrowstyle='<-')
    font = FontProperties(fname=r'C:\Windows\Fonts\STXINGKA.TTF', size=15)
    create_plot.ax1.annotate(node_txt, xy=parent_pt,  xycoords='axes fraction', xytext=center_pt,
                            textcoords='axes fraction', va="center", ha="center", bbox=node_type,
                            arrowprops=arrow_args, FontProperties=font)

# 标注划分属性
def plot_mid_text(cntr_pt, parent_pt, txt_str):
    font = FontProperties(fname=r'C:\Windows\Fonts\MSYH.TTC', size=10)
    x_mid = (parent_pt[0] - cntr_pt[0]) / 2.0 + cntr_pt[0]
    y_mid = (parent_pt[1] - cntr_pt[1]) / 2.0 + cntr_pt[1]
    create_plot.ax1.text(x_mid, y_mid, txt_str, va="center", ha="center", color='red', FontProperties=font)

# 绘制决策树
def plot_tree(decision_tree, parent_pt, node_txt):
    d_node = dict(boxstyle="sawtooth", fc="0.8")
    leaf_node = dict(boxstyle="round4", fc='0.8')
    num_leafs = get_num_leafs(decision_tree)
    first_str = next(iter(decision_tree))
    cntr_pt = (plot_tree.xoff + (1.0 +float(num_leafs))/2.0/plot_tree.totalW, plot_tree.yoff)
    plot_mid_text(cntr_pt, parent_pt, node_txt)
    plot_node(first_str, cntr_pt, parent_pt, d_node)
    second_dict = decision_tree[first_str]
    plot_tree.yoff = plot_tree.yoff - 1.0/plot_tree.totalD
    for k in second_dict.keys():
        if isinstance(second_dict[k], dict):
            plot_tree(second_dict[k], cntr_pt, k)
        else:
            plot_tree.xoff = plot_tree.xoff + 1.0/plot_tree.totalW
            plot_node(second_dict[k], (plot_tree.xoff, plot_tree.yoff), cntr_pt, leaf_node)
            plot_mid_text((plot_tree.xoff, plot_tree.yoff), cntr_pt, k)
    plot_tree.yoff = plot_tree.yoff + 1.0/plot_tree.totalD

def create_plot(dtree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    create_plot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plot_tree.totalW = float(get_num_leafs(dtree))
    plot_tree.totalD = float(get_tree_depth(dtree))
    plot_tree.xoff = -0.5/plot_tree.totalW
    plot_tree.yoff = 1.0
    plot_tree(dtree, (0.5, 1.0), '')
    plt.show()

create_plot(mytree)