SinGAN: Learning a Generative Model from a Single Natural Image——ICCV2019最佳论文详解
SinGAN:Learning a Generative Model from a Single Natural Image
- 论文亮点
- 研究背景
- 研究方法与意义
- 方法细节
- 多尺度结构
- 训练
- 对抗损失
- 重建损失
- 实验与结果
- 在测试时Scales的影响
- 在训练时Scales的影响
- 应用场景
- 超分辨率
- 剪切画到图像的翻译
- 目标融合
- 图像编辑
论文亮点
- 最大的亮点在于其训练样本是单张自然图像,而不是一个训练图像集。
- 无条件的GAN,从噪声中合成图像。
- 作者给出了许多任务场景下SinGAN的应用
研究背景
生成对抗网络已经在建模视觉数据的高维分布上取得了引人注目的进展。特别是当在特定类别的数据集上训练时,无条件GAN在生成逼真、高质量的样本上展现出了卓越效果。然而,从带有多种目标类别的高度多样化数据捕捉数据分布(比如ImageNet)仍然被认为是一个巨大的挑战,并且通常需要条件输入或者是仅在一个特定类别上训练。
在这里,我们将GAN的使用引入一个新的领域——从单张自然图像学习到的无条件生成。
在之前的基于单张图像的深度学习模型(或者是few-shot learning,少样本学习)中,它们通常是有条件的(即输入是一张图像,进行图像—图像的转换)。而作者提出的SinGAN是无条件的(从噪声中生成图像),区别于其他只能应用于生成纹理图像内容的无条件GAN,SinGAN不限制于纹理生成并且可以处理一般的自然图像。
区别与其他图像处理领域的生成模型,它们常常在一个特定类的训练集上训练。而SinGAN并不对捕捉同类图像中的共同特征感兴趣,而是考虑训练数据中(一张图像)的不同来源——在单张自然图像的不同尺度上所有的overlapping patches(部分重叠patch)。
研究方法与意义
我们引入了SinGAN,一个可以从单张自然图像中学习的无条件生成模型。我们的模型被训练于捕捉图像中patch的内在分布,然后可以生成与训练图像视觉内容一致的高质量、多样的样本。SinGAN包含了一个全卷积GAN的金字塔,其中每一个GAN都负责从图像不同的尺度上学习到patch分布。这允许生成带有任意大小和长宽比的新样本。相比于之前的单张图像GAN方法,我们的方法不仅仅适用于纹理图像,并且是无条件的(可以从噪声中直接生成新样本,不需要像Conditional GAN中一样引入其他条件输入,或是从图像到图像的翻译)。用户的研究确认了生成样本经常与真实图像混淆。我们举例说明了SinGAN在广阔的图像操作任务上的应用。
方法细节
我们的目标是学习一个无条件的生成对抗网络,它可以捕捉单张训练图像的内在统计量。这个任务和传统的GAN设定在概念上很相似,除了这里使用的训练样本只有一个,而不是整张图像都作为训练样本。
我们选择跳出纹理合成,来解决更多的自然图像问题。这需要在不同尺度上捕捉复杂图像结构的统计量。比如,我们希望捕捉图像的全局属性(例如布局、大目标的形状,比如顶部的天空和底部的地面),或者是捕捉其他细节和纹理信息。

我们的生成框架如上图所示,它由一系列的PatchGAN组成,其中每一个负责捕捉输入图像不同尺度的Patch分布。
多尺度结构
具体来说,我们的模型由一个生成器金字塔 { G 0 , … , G N } \left\{G_{0}, \ldots, G_{N}\right\} {G0,…,GN}组成,针对输入图像 x x x的金字塔 { x 0 , … , x N } \left\{x_{0}, \dots, x_{N}\right\} {x0,…,xN}进行训练,其中 x n x_{n} xn是输入图像 x x x通过一个变化因子 r n r^{n} rn的下采样版本,并且 r > 1 r>1 r>1。每一个生成器 G n G_{n} Gn负责生成与相应输入图像 x n x_{n} xn的Patch分布相关的逼真图像样例。这是通过对抗学习实现的,其中 G n G_{n} Gn学会去愚弄一个判别器 D n D_{n} Dn,而判别器尝试着去区分在生成样本中的Patch和输入图像 x n x_{n} xn的Patch。
一张图像样例的生成从粗略的尺度上开始,依次地通过所有生成器直到最精细的尺度,并且在每一个尺度上都有噪声注入。所有的生成器和判别器有相同的感受野,并且因此随着我们生成过程的进行,捕捉到的结构尺度也不断减少。在最粗略的尺度(图像分辨率最大,也是最开始的层),生成过程就是纯粹的生成,即 G N G_{N} GN将空间白高斯噪声 z N z_{N} zN映射到一个图像样例 x ~ N \tilde{x}_{N} x~N上。
x ~ N = G N ( z N ) \tilde{x}_{N}=G_{N}\left(z_{N}\right) x~N=GN(zN)
在这层上的有效感受野是典型的图像高度的 ∼ 1 / 2 \sim 1 / 2 ∼1/2,因此 G N G_{N} GN生成图像一般布局与目标全局结构。每一个更精细的生成器 G n G_{n} Gn(其中 n < N n
x ~ n = G n ( z n , ( x ~ n + 1 ) ↑ r ) , n < N \tilde{x}_{n}=G_{n}\left(z_{n},\left(\tilde{x}_{n+1}\right) \uparrow^{r}\right), \quad n
所有的生成器都有相同的结构,如下图所示。
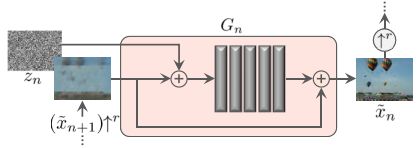
具体来说,噪声 z n z_{n} zn被添加到上采样图像 ( x ~ n + 1 ) ↑ r \left(\tilde{x}_{n+1}\right) \uparrow^{r} (x~n+1)↑r中,然后被送入一系列的卷积层。这确保了GAN不会忽视噪声,而这种情况常常在包含随机性的有条件GAN中发生。卷积层的角色是生成在 ( x ~ n + 1 ) ↑ r \left(\tilde{x}_{n+1}\right) \uparrow^{r} (x~n+1)↑r中缺失的细节(残差学习)。即, G n G_{n} Gn执行如下操作:
x ~ n = ( x ~ n + 1 ) ↑ r + ψ n ( z n + ( x ~ n + 1 ) ↑ r ) \tilde{x}_{n}=\left(\tilde{x}_{n+1}\right) \uparrow^{r}+\psi_{n}\left(z_{n}+\left(\tilde{x}_{n+1}\right) \uparrow^{r}\right) x~n=(x~n+1)↑r+ψn(zn+(x~n+1)↑r)
其中 ψ n \psi_{n} ψn是全卷积网络,带有5个卷积块,每个块由Conv(3x3)-BatchNorm-LeakyReLU组成。我们在最粗略的尺度上从32个卷积核开始,每隔4个尺度增加2倍。因为生成器是全卷积的,我们可以通过改变噪声图的维度,生成任意尺寸和长宽比的图像。
训练
我们依次地训练我们的多尺度结构模型,从最粗略的GAN到最精细的GAN。一旦一个GAN被训练好,那么它就保持固定。对第n个GAN我们的训练Loss由一个对抗项和一个重建项组成:
min G n max D n L a d v ( G n , D n ) + α L r e c ( G n ) \min _{G_{n}} \max _{D_{n}} \mathcal{L}_{\mathrm{adv}}\left(G_{n}, D_{n}\right)+\alpha \mathcal{L}_{\mathrm{rec}}\left(G_{n}\right) GnminDnmaxLadv(Gn,Dn)+αLrec(Gn)
其中,对抗项损失 L a d v \mathcal{L}_{\mathrm{adv}} Ladv惩罚了输入图像 x n x_{n} xn的Patch分布与生成样本 x ~ N \tilde{x}_{N} x~N的Patch分布的距离。而重建损失 L r e c \mathcal{L}_{\mathrm{rec}} Lrec则用于确保可以产生 x n x_{n} xn的噪声图的特定集的存在,这是一项对于图像处理任务非常重要的特征。
对抗损失
使用了WGAN-GP损失。损失函数是定义在整个图像上的,而不是随机取的Patch上的。
重建损失
我们想要确保存在一个输入噪声图的特定集,可以生成原始图像 x x x。我们具体选择了 { z N r e c , z N − 1 r e c , … , z 0 r e c } = { z ∗ , 0 , … , 0 } \left\{z_{N}^{\mathrm{rec}}, z_{N-1}^{\mathrm{rec}}, \ldots, z_{0}^{\mathrm{rec}}\right\}=\left\{z^{*}, 0, \ldots, 0\right\} {zNrec,zN−1rec,…,z0rec}={z∗,0,…,0},其中 z ∗ z^{*} z∗是一些固定的噪声图(在训练中保持固定)。当使用这些噪声图时,用 x ~ n r e c \tilde{x}_{n}^{\mathrm{rec}} x~nrec表示在第n个尺度上生成的图像。然后对于 n < N n
对于 n = N n=N n=N,我们使用 L r e c = ∥ G N ( z ∗ ) − x N ∥ 2 \mathcal{L}_{\mathrm{rec}}=\left\|G_{N}\left(z^{*}\right)-x_{N}\right\|^{2} Lrec=∥GN(z∗)−xN∥2。
重建图像 x ~ n r e c \tilde{x}_{n}^{\mathrm{rec}} x~nrec在训练中还有另一个角色,用于定义在每个尺度中的噪声 z n z_{n} zn标准差 σ n \sigma_{n} σn。具体地,我们将 σ n \sigma_{n} σn正比于 x n x_{n} xn和 ( x ~ n + 1 ) ↑ r \left(\tilde{x}_{n+1}\right) \uparrow^{r} (x~n+1)↑r之间的根均方误差(RMSE),它给出了一个需要在这个尺度添加的细节数量的指示。
实验与结果
在以下的各种实验中,我们发现SinGAN可以描述新的逼真结构和目标布局,同时保留训练图像的视觉内容。在成功保留目标的全局结构的情况下(例如下图的山),由于网络的感受野较小(比整张图像要小),SinGAN可以生成在训练图像中不存在的新的patch组合。并且SinGAN的结构是分辨率无关的,因此可以用在高分辨率图像上。在这里,所有尺度上的结构都被很好地生成了。
在测试时Scales的影响
我们多尺度的结构允许控制样本间的可变性,通过选择在测试时开始生成的尺度。在 n n n尺度下开始,我们固定这个尺度下的噪声图为 { z N r e c , … , z n + 1 r e c } \left\{z_{N}^{\mathrm{rec}}, \ldots, z_{n+1}^{\mathrm{rec}}\right\} {zNrec,…,zn+1rec},并且从 { z n , … , z 0 } \left\{z_{n}, \ldots, z_{0}\right\} {zn,…,z0}随机抽取。其影响如下图所示:

如图所示,从最粗略的尺度 n = N n=N n=N开始会导致全局结构的大变化。以上图的斑马为例,生成了不真实的图像。并且,从越精细的尺度开始生成,可以保持全局结构的完整性,同时仅改变一些图像的精细特征。
在训练时Scales的影响
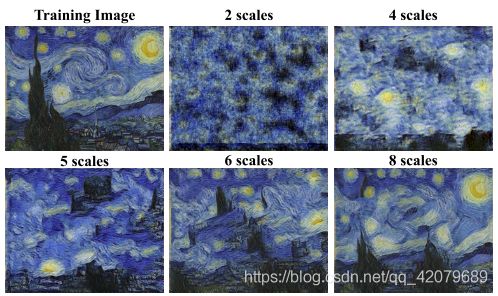
上图展示了在训练时用一些尺度的影响。当尺度较小的时候,在最粗略的层次上的有效感受野较小,这仅仅允许捕捉精细的纹理。当尺度的数量增加时,全局目标布局更好地被保留。

上图展示了从单张训练图像中学习到的图像生成。作者提出了SinGAN——一种在单张自然图像上训练的新的无条件生成模型。该模型使用一种专用的多尺度对抗训练策略,在多个尺度下学习图像的Patch统计信息。它可以被用于生成保留原始patch分布的新的且逼真的图像样例,同时创造新的目标布局和结构。

上图展示了SinGAN在不同的图像处理任务中的应用,包括:将一张画作转换为一张真实图像,重新布局和编辑图像中的目标,将一个新的目标融入到图像中,图像超分辨率和从单张输入中创造一个动画。第一行是训练图像,第二行是测试图像,第三行是输出结果。

上图展示了随机图像样例。在单张图像上训练SinGAN后,我们的模型可以生成逼真的随机图像样本,它描述了新的结构和目标布局,但也保留了训练图像的patch分布。因为我们的模型是全卷积的,生成的图像可以有任意的大小和长宽比。注意到我们的目标不是图像重定向(这是一项在不引入大的畸变的情况下,通过改变照片的大小和比例信息,来适应各种尺寸屏幕的技术)——我们的图像样例是随机的并且朝着保持patch统计信息进行优化的,而不是保留图像中显著的目标。

上图展示了高分辨率图像生成案例。展示了一个由我们的模型生成的随机样本,在 243 × 1024 243 \times 1024 243×1024图像上进行训练(如右上角所示),逼真地生成了新的全局结构和良好的细节。
应用场景
我们将SinGAN用于一系列的图像处理任务中。对所有的应用,我们使用了相同的模型结构,并且没有任何进一步的调整
超分辨率

超分辨率应用场景,当SinGAN被训练于低分辨率图像时,我们可以进行超分辨率。这是通过迭代地上采样图像,并将它喂给SinGAN最合适的尺度生成器实现的。正如所看到的,正如所看到的,SinGAN的视觉质量相比SOTA的内部方法ZSSR和DIP都要好。它也比EDSR要好,并且可以与SRGAN这些在大的数据集上训练的模型相媲美。图中的指标分别是PSNR与NIQE。
剪切画到图像的翻译
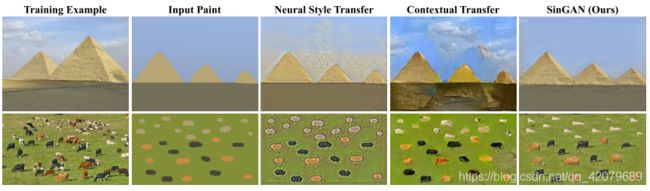
上图展示了画作(第二列)到图像的翻译应用场景。我们在目标图像上训练SinGAN并且在测试的时候将画作的下采样版本输入一个粗略的水平。我们生成的图像保留了剪切画的布局和一般结构,同时也生成了可以匹配训练图像的逼真纹理和良好细节。在这项任务中,著名的风格迁移模型宣告失败。

