使用opencv进行相机标定(python)

前言
今天介绍一个比较复杂的话题——照相机标定
为社么会复杂呢？因为解释起来比较麻烦，会涉及到很多数学公式。
本文将运用张正友相机标定的数学原理，并给出标定流程。OpenCV中已经封装好了一系列函数，我们使用这些函数可以实现张正友相机标定。那么首先说明一下什么是相机标定？
一个摄像机可以大致分为三个部分：镜头 、感光元件（CCD和CMOS）、处理电路。当光线透过镜头，会在感光元件上形成一个物体的“像”。（小孔成像原理）然后经过一系列处理就变成了电子版的图片。当然这种变换过程中会产生一定的误差（就好像透过猫眼看人会是一个曲面）。所以为了消除或者矫正这些误差，就出现了标定技术（就是将图片还原成正常人眼看到的图像）。

相机标定步骤

1. 准备一张打印好的棋盘格，对棋盘格进行不同角度的拍摄，10-20张图片为宜；
2. 对每张图片提取角点信息；
3. 在图片中画出提取出的角点；
4. 相机标定；
5. 对标定结果评价，计算误差；
6. 使用标定结果对原图片进行矫正；

一 、摄像机标定成像原理
1.四个坐标系
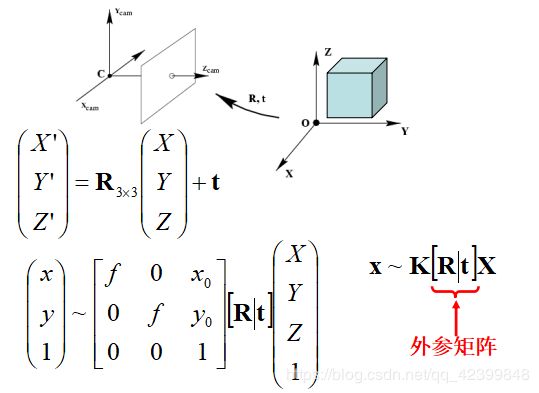
世界坐标系、相机坐标系、像素坐标系、成像平面坐标系。
我们可以把现实生活遇到的任何事物用坐标系表示出来，也可以用坐标系表示整个世界，于是便建立起了世界坐标系。想象一下，摄像机拍摄的是一张二维图片，因此整个摄像机可以用一个坐标系去标识它获取到的某个物体的位置，这是相机坐标系。像素坐标系就是相片的坐标系。成像平面坐标系类似于像素坐标系。
原本我们期望的拍摄效果：是每个坐标系中的像素都相互对应，类似于一种一元一次方程，但由于镜头或者其他关系，现在这条“直线”弯了，得到的图像也会出现“弯曲”，因此我们需要把它矫正。

2.相机参数
相机都有不同的内部参数、外部参数；

内部参数:有一个参数矩阵（fx,fy,cx,cy)和一个畸变系数(三个径向k1,k2,k3;两个切向p1,p2)；内部参数是唯一的，就是一部相机只有一组内部参数。
相机将场景中的三维点变换为图像中的二维点，也就是各个坐标系变换的组合，可将变换过程整理为矩阵相乘的形式：

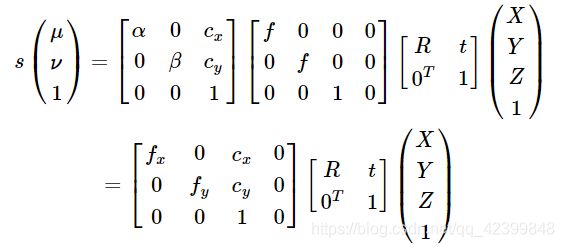
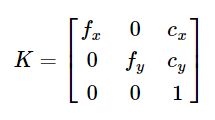
其中，α,β表示图像上单位距离上像素的个数，则fx=αf,fy=βf将相机的焦距f变换为在x,y方向上像素度量表示。
另外，为了不失一般性，可以在相机的内参矩阵上添加一个扭曲参数γ，该参数用来表示像素坐标系两个坐标轴的扭曲。则内参数K变为

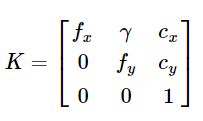
外部参数： 摄像机在世界坐标系中的位姿，由摄像机与世界坐标系的相对位姿关系决定。其参数有：旋转向量R（大小为1x3的矢量或旋转矩阵3x3）和平移向量T(Tx,Ty,Tz)；对不同的标定图，外部参数也是不同的，就是外部参数不唯一，你拿了多少不同的图去标定就会有多少不同的外部参数。

3.标定结束
标定完成后，你会得到标定的内部参数，标定完之后就可以直接用内参数和畸变参数得到畸变校正图像。接下来就可以使用OpenCV了，即用内参数和畸变参数作为initUndistortRectifyMap()函数的输入，得到原图像与畸变校正图像的x,y坐标映射关系，即两个变换矩阵。再以这两个变换矩阵作为remap()函数的输入，得到畸变校正图像。

二、消除径向畸变
为了取得好的成像效果，通常要在相机的镜头前添加透镜。在相机成像的过程中，透镜会对光线的传播产生影响，从而影响相机的成像效果，产生畸变：

透镜自身的形状对才光线的传播产生影响，形成的畸变称为径向畸变。在小孔模型中，一条指向在成像平面上的像仍然是直线。但是在实际拍摄的过程中，由于透镜的存在，往往将一条直线投影成了曲线，越靠近图像的边缘，这种现象越明显。透镜往往是中心对称的，使得这种不规则的畸变通常是径向对称的。主要有两大类：桶形畸变和枕形畸变。如下图所示

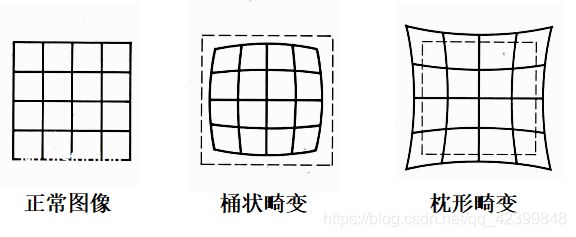
桶状畸变由中短焦造成，枕形畸变由长焦造成。
设，(μ,ν)是理想的无畸变的像素坐标；(μ^ ,v^ )是畸变后的像素坐标；(μ0,ν0)是相机的主点；(x,y)和(x^ ,y^)理想的无畸变的归一化的图像坐标和畸变后的归一化图像坐标，使用下面的式子表示径向畸变：

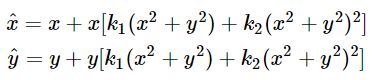
径向畸变的中心和相机的主心是在相同的位置

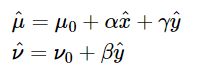
假设γ=0，以矩阵形式则有：

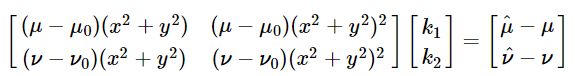
上面的等式是从一幅图像上的一个点取得，设有n幅图像，每幅图像上有m个点，则将得到的所有等式组合起来，可以得到2mn个等式，将其记着矩阵形式
则可得：
利用最大似然估计取得最优解，使用LM的方法估计使得下面式子是最小值的参数值：

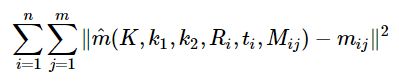
得到畸变参数k1,k2后，可以先将图像进行去畸变处理，然后用去畸变后的图像坐标估计相机的内参数。

三、opencv中张正友的相机标定
算法实现：
1.准备图片

2.提取角点信息；
为了找到棋盘格模板，可使用openCV中的函数cv2.findChessboardCorners()。需要告诉程序标明模板是何规格，我使用的是1311的棋盘格，含有1210的内部角点。这个函数如果检测到模板，会返回对应的角点，并返回true。当然不一定所有的图像都能找到需要的模板，所以我们可以使用多幅图像进行定标。

3.画出角点；
找到角点后，我们可以使用cv2.cornerSubPix()可以得到更为准确的角点像素坐标。我们也可以使用cv2.drawChessboardCorners()将角点绘制到图像上显示。如下图所示：

4.相机标定；
通过前面的步骤，得到了用于标定的三维点和与其对应的图像上的二维点对。我们使用cv2.calibrateCamera()进行标定，这个函数会返回标定结果、相机的内参数矩阵、畸变系数、旋转矩阵和平移向量。
5.计算误差
通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差，这个值就是反投影误差

6.矫正图像
使用cv2.undistort()方法去除畸变

代码
我的手机型号是HUAWEI P20 Pro 拍了10张图片
所有步骤代码如下：

import cv2
import glob
import numpy as np

#棋盘规格
cbraw = 11
cbcol = 9
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((cbraw*cbcol,3), np.float32) 
'''
设定世界坐标下点的坐标值，因为用的是棋盘可以直接按网格取；
假定棋盘正好在x-y平面上，这样z=0，简化初始化步骤。
mgrid把列向量[0:cbraw]复制了cbcol列，把行向量[0:cbcol]复制了cbraw行。
转置reshape后，每行都是9*11网格中的某个点的坐标。
'''
objp[:,:2] = np.mgrid[0:cbraw,0:cbcol].T.reshape(-1,2)

objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
#glob是个文件名管理工具
images = glob.glob("E:/image/Ex4/*.jpg")
for fname in images:
#对每张图片，识别出角点，记录世界物体坐标和图像坐标
    img = cv2.imread(fname) #source image
    #我用的图片太大，缩小了一半
    img = cv2.resize(img,None,fx=0.5, fy=0.5, interpolation = cv2.INTER_CUBIC)
    gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #转灰度
    #cv2.imshow('img',gray)
    #cv2.waitKey(1000)
    #寻找角点，存入corners，ret是找到角点的flag
    ret, corners = cv2.findChessboardCorners(gray,(11,9),None)
    #criteria:角点精准化迭代过程的终止条件
    criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
    #执行亚像素级角点检测
    corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)

    objpoints.append(objp)
    imgpoints.append(corners2)
    #在棋盘上绘制角点,只是可视化工具
    img = cv2.drawChessboardCorners(gray,(11,9),corners2,ret)
    cv2.imshow('img',img)
    #cv2.waitKey(1000)
'''
传入所有图片各自角点的三维、二维坐标，相机标定。
每张图片都有自己的旋转和平移矩阵，但是相机内参和畸变系数只有一组。
mtx，相机内参；dist，畸变系数；revcs，旋转矩阵；tvecs，平移矩阵。
'''
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)
img = cv2.imread('E:/image/Ex4/1.jpg')
#注意这里跟循环开头读取图片一样，如果图片太大要同比例缩放，不然后面优化相机内参肯定是错的。
img = cv2.resize(img,None,fx=0.5, fy=0.5, interpolation = cv2.INTER_CUBIC)
h,w = img.shape[:2]
'''
优化相机内参（camera matrix），这一步可选。
参数1表示保留所有像素点，同时可能引入黑色像素，
设为0表示尽可能裁剪不想要的像素，这是个scale，0-1都可以取。
'''
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
#纠正畸变
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)

#输出纠正畸变以后的图片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('Ex4result.png',dst)
#打印我们要求的两个矩阵参数
print ("newcameramtx:\n",newcameramtx)
print ("dist:\n",dist)
#计算误差
tot_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    tot_error += error

print ("total error: ", tot_error/len(objpoints))

实现结果：

焦距分别是961.88232422，968.19952393