Python练习题:矩阵乘法(选自蓝桥杯)
题目要求:
给定一个N阶矩阵A,输出A的M次幂(M是非负整数)
输入格式
第一行是一个正整数N、M(1<=N<=30, 0<=M<=5),表示矩阵A的阶数和要求的幂数
接下来N行,每行N个绝对值不超过10的非负整数,描述矩阵A的值
输出格式
输出共N行,每行N个整数,表示A的M次幂所对应的矩阵。相邻的数之间用一个空格隔开
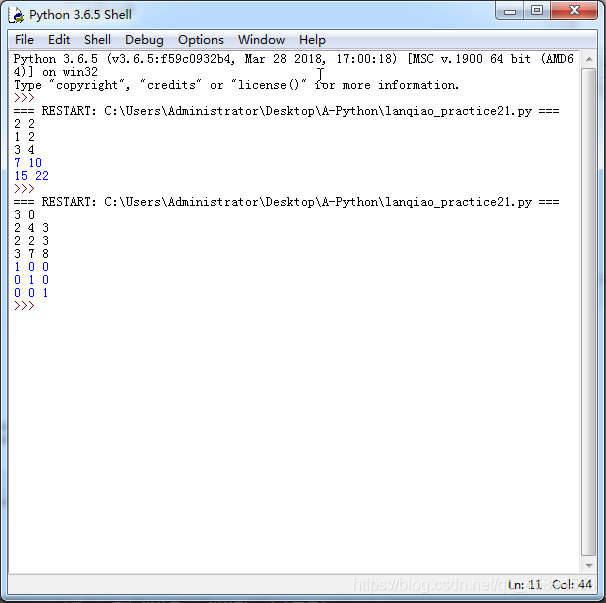
样例输入
2 2
1[0,0] 2[0,1] 1[0,0] 2[0,1]
3[1,0] 4[1,1] 3[1,0] 4[1,1]
样例输出11+23 12+24
7 10
15 22
问题分析:
为了让代码简单易懂,在这个题直接采用了创建类方法,将需要实现的功能赋予类的各个函数,可以将矩
阵看两层的元列表list[][],以及根据矩阵相乘的运算规则,将矩阵乘法运算分解成矩阵翻转MatrixReversal()
以及矩阵的相乘运算MatrixMultiplication(),最后再设计一个函数将矩阵的输出PrintMatrix()
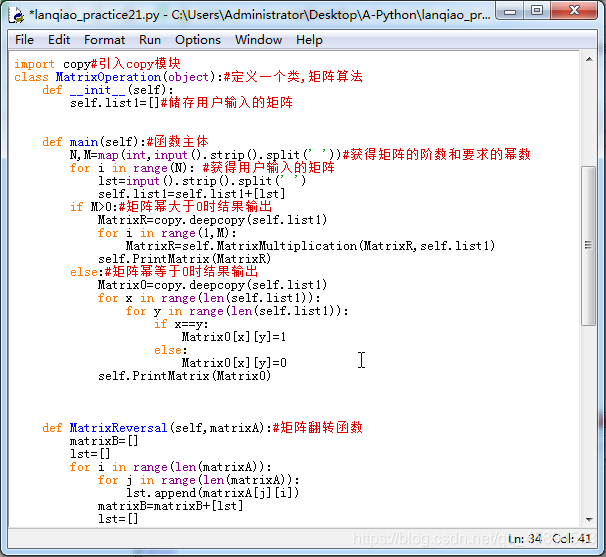
代码图:
代码如下:
import copy#引入copy模块
class MatrixOperation(object):#定义一个类,矩阵算法
def __init__(self):
self.list1=[]#储存用户输入的矩阵
def main(self):#函数主体
N,M=map(int,input().strip().split(' '))#获得矩阵的阶数和要求的幂数
for i in range(N): #获得用户输入的矩阵
lst=input().strip().split(' ')
self.list1=self.list1+[lst]
if M>0:#矩阵幂大于0时结果输出
MatrixR=copy.deepcopy(self.list1)
for i in range(1,M):
MatrixR=self.MatrixMultiplication(MatrixR,self.list1)
self.PrintMatrix(MatrixR)
else:#矩阵幂等于0时结果输出
Matrix0=copy.deepcopy(self.list1)
for x in range(len(self.list1)):
for y in range(len(self.list1)):
if x==y:
Matrix0[x][y]=1
else:
Matrix0[x][y]=0
self.PrintMatrix(Matrix0)
def MatrixReversal(self,matrixA):#矩阵翻转函数
matrixB=[]
lst=[]
for i in range(len(matrixA)):
for j in range(len(matrixA)):
lst.append(matrixA[j][i])
matrixB=matrixB+[lst]
lst=[]
return matrixB
def MatrixMultiplication(self,matrixA,matrixB):#两个矩阵的乘法运算
matrixC=copy.deepcopy(matrixA)
matrixB=self.MatrixReversal(matrixB)
x,y,Sum=0,0,0
while x<len(matrixA):
for i in range(len(matrixB)):
count=0
for num in matrixB[i]:
Sum=Sum+int(matrixA[x][count])*int(num)
count+=1
matrixC[x][y]=Sum
Sum,count=0,0
if y==len(matrixA[x])-1:
y=0
else:
y+=1
x+=1
return matrixC
def PrintMatrix(self,matrix):#矩阵输出函数
for x in range(len(matrix)):
for y in range(len(matrix[0])):
if y<len(matrix[0])-1:
print(matrix[x][y],end=' ')
else:
print(matrix[x][y])
matrix_operation=MatrixOperation()
matrix_operation.main()