《机器学习实战》（五）---支持向量机

引入

支持向量机是学习这些算法以来，数学最难，代码最长的一个，数学推导极其之长，非常感谢B站up shuhuai008的白板推导系列，如果没有看过数学推导部分或者看了其他资料没有看懂的同学，一定要去看up的视频，讲的非常详细。我这一章的东西绝大部分都是来自up和《统计学习方法》的内容。
支持向量机又称SVM，也是一种分类算法，它和上一章的逻辑回归比较像，即便是书上的例子也很像，都是利用超平面划分数据点，但是两者也有些许不同。希望经过这一章的在学习，我能对这两种算法有更深刻的认识。
SVM有三宝：间隔、对偶、核技巧
又根据分类方法的不同，又分为硬间隔、软间隔、核技巧
《机器学习实战》主要介绍了一种基于SVM的算法-SMO

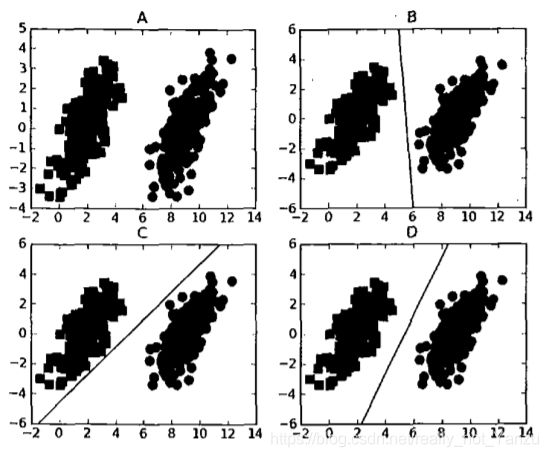
又是这样的两种类别的数据，怎样的超平面才能得到最好的效果呢？，这个图不是很清晰，用《统计学习方法》里的一张图。同时我们引入几个概念。

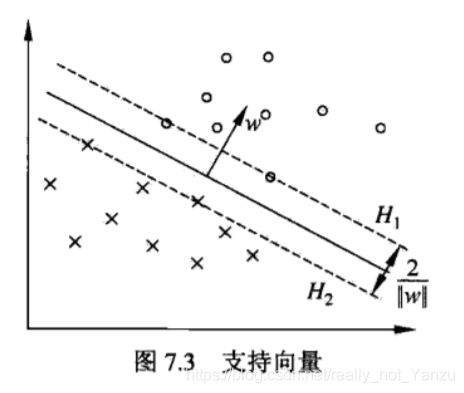
支持向量：训练集中样本点中距离超平面最近的点的实例
间隔边界：图中H1,H2就是间隔边界，支持向量在他们身上，间隔边界平行于超平面
最大间隔： H1，H2之间的距离叫做间隔，我们要找的就是最大间隔。
SVM最简单的硬间隔就是基于这个想法，可以对数据分类的超平面有无线多个，但是使间隔最大的超平面只有一个，我们就寻找一个能使间隔最大的超平面作为分类结果，这个例子比较的特殊，两类别之间有明显的界限，且没有很强的噪音，用哪个分类方式应该都不会太差…但大部分的是没有这么理想的数据集的，硬间隔在数据没有这么理想的时候分类效果可能不是很好，因此会用到软间隔。后面的软间隔只是在这个硬间隔基础上加了一个Loss函数。我们首先先进行硬间隔的数学理论推导部分

数学推导

硬间隔

对于数据集

我们设超平面为 wx+b=0，超平面一侧为正例，另一侧为负例，通过计算分类决策函数f(x),结果为正值时分类到正例，结果为负值时分类到负例。
既然是最大求间隔，那么怎么计算点到超平面的距离呢，
https://blog.csdn.net/yutao03081/article/details/76652943，这是理论推导。
根据上面可得，对于数据点，存在

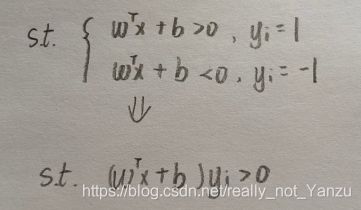
这样写实在是太麻烦了，后面等我买个ipad，有机会再在上面推导一次录个视频发一下，我把我当时记的笔记发上来，不好理解的地方去看视频吧…

软间隔

简易SMO算法

# version:python3.7.3
# author:hty
# date:2020.5.22

from numpy import *
from time import sleep

def loadDataSet(filename):
	'''
	function:加载数据集
	'''
    dataMat = []
    labelMat = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


def selectJrand(i,m):
	'''
	function:返回一个值不等于i，并且值 0
    j=i
    while (j==i):
        j = int(random.uniform(0,m))
    return j

def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
	'''
	function:简易SMO算法
	dataMatIn:数据集
	classLabels:数据点对应类别
	C:常数C
	toler:容错率
	maxIter:循环取消前最大循环次数
	'''
	# 转化为矩阵形式
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
    # 初始化b，得到矩阵行数跟列数
    b = 0; m,n = shape(dataMatrix)
	# 初始化a矩阵
    alphas = mat(zeros((m,1)))
	# iter是迭代次数
    iter = 0
    # 当小于最大迭代次数时
    while (iter < maxIter):
    	# alphaPairsChanged 用于判断是否有alpha被优化
        alphaPairsChanged = 0
        for i in range(m):
       		# 这里就是在我们知道w值的情况下，带入wx+b，即对应 ∑alpha_i*y_i* + b，预测xi的类别，这里不太好理解，可以自己拿笔写一写
            fXi = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[i, :].T)) + b
            # 求真实值和预测值的差值
            Ei = fXi - float(labelMat[i])
			# toler：容忍错误的程度
            # labelMat[i]*Ei < -toler 则需要alphas[i]增大，但是不能>=C
            # labelMat[i]*Ei > toler 则需要alphas[i]减小，但是不能<=0
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
            	# 挑选另一个j
                j = selectJrand(i, m)
				# 计算j的预测值
                fXj = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j, :].T)) + b
                # 计算j真实值和预测值的差值
                Ej = fXj - float(labelMat[j])
				# 拷贝i，j对应的alpha值
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                # 这是要满足KKT条件，对alpha设下的界
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                # 如果下界等于上界，说明alpha = 0
                if L == H: print ("L==H"); continue
                # 算出 eta = K11 + K22 - K12
                eta = 2.0 * dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]* dataMatrix[j, :].T
                #print('eta:',eta)
                if eta >= 0: print("eta>=0"); continue
                # 计算更新后的alpha[j]
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                # 要求alpha[j]满足KKT条件
                alphas[j] = clipAlpha(alphas[j], H, L)
                # 如果alpha[j]变化不大，说明优化已经稳定，进入下一个for循环
                if (abs(alphas[j] - alphaJold) < 0.00001): print ("j not moving enough"); continue
                # 更新完alpha[j]再更新alpha[i]，公式来自《统计学习方法》7.109公式
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
                # 公式来自7.115
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[i, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i, :]*dataMatrix[j, :].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[j, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j, :]*dataMatrix[j, :].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                # 如果一次循环能运行到这里，说明alpha已经更新
                alphaPairsChanged += 1
                print ("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
        # 如果为0，说明这一次外循环没有变动
        if (alphaPairsChanged == 0): iter += 1
        # 如果alpha有更新，那么重新进行外循环
        else: iter = 0
        print( "iteration number: %d" % iter)
   	# 返回alpha的列向量和b
    return b, alphas

上面这个是简易smo算法，下面的是完整版的smo算法

完整SMO算法

不想看了，太麻烦了…来源于https://www.cnblogs.com/gezhuangzhuang/p/9965819.html

class optStruct:
    """
    Function：   存放运算中重要的值

    Input：      dataMatIn：数据集
                classLabels：类别标签
                C：常数C
                toler：容错率

    Output： X：数据集
                labelMat：类别标签
                C：常数C
                tol：容错率
                m：数据集行数
                b：常数项
                alphas：alphas矩阵
                eCache：误差缓存
    """ 
    def __init__(self, dataMatIn, classLabels, C, toler):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m, 1)))
        self.b = 0
        self.eCache = mat(zeros((self.m, 2)))

def calcEk(oS, k):
    """
    Function：   计算误差值E
	
    Input：      oS：数据结构
                k：下标
    Output： Ek：计算的E值
    """ 
    # 计算fXk，整个对应输出公式f(x)=w`x + b
    fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k,:].T)) + oS.b   
    # 计算E值
    Ek = fXk - float(oS.labelMat[k])
    # 返回计算的误差值E
    return Ek
def selectJ(i, oS, Ei):
    """
    Function：   选择第二个alpha的值
    Input：      i：第一个alpha的下标
                oS：数据结构
                Ei：计算出的第一个alpha的误差值
    Output： j：第二个alpha的下标
                Ej：计算出的第二个alpha的误差值
    """ 
    #初始化参数值
    maxK = -1; maxDeltaE = 0; Ej = 0
    #构建误差缓存
    oS.eCache[i] = [1, Ei]
    #print('oS.eCache[:, 0]:',oS.eCache[:, 0])
    #构建一个非零列表，返回值是第一个非零E所对应的alpha值，而不是E本身
    validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
    print('validEcacheList:',validEcacheList)
    #如果列表长度大于1，说明不是第一次循环
    if (len(validEcacheList)) > 1:
        #遍历列表中所有元素
        for k in validEcacheList:
            #如果是第一个alpha的下标，就跳出本次循环
            if k == i: continue
            #计算k下标对应的误差值
            Ek = calcEk(oS, k)
            #取两个alpha误差值的差值的绝对值
            deltaE = abs(Ei - Ek)
            #最大值更新
            if (deltaE > maxDeltaE):
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        #返回最大差值的下标maxK和误差值Ej
        return maxK, Ej
    #如果是第一次循环，则随机选择alpha，然后计算误差
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    #返回下标j和其对应的误差Ej
    return j, Ej
    
def updateEk(oS, k):
    """
    Function：   更新误差缓存
    Input：      oS：数据结构
                j：alpha的下标
    Output： 无
    """ 
    #计算下表为k的参数的误差
    Ek = calcEk(oS, k)
    #将误差放入缓存
    oS.eCache[k] = [1, Ek]
    
def innerL(i, oS):
    """
    Function：   完整SMO算法中的优化例程

    Input：      oS：数据结构
                i：alpha的下标

    Output： 无
    """ 
    #计算误差
    Ei = calcEk(oS, i)
    #如果标签与误差相乘之后在容错范围之外，且超过各自对应的常数值，则进行优化
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        #启发式选择第二个alpha值
        j, Ej = selectJ(i, oS, Ei)
        #利用copy存储刚才的计算值，便于后期比较
        alphaIold = oS.alphas[i].copy(); alpahJold = oS.alphas[j].copy();
        #保证alpha在0和C之间
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS. alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        # 如果界限值相同，则不做处理直接跳出本次循环
        if L == H: print("L==H"); return 0
        #最优修改量，求两个向量的内积（核函数）
        eta = 2.0 * oS.X[i, :]*oS.X[j, :].T - oS.X[i, :]*oS.X[i, :].T - oS.X[j, :]*oS.X[j, :].T
        #如果最优修改量大于0，则不做处理直接跳出本次循环，这里对真实SMO做了简化处理
        if eta >= 0: print("eta>=0"); return 0
        #计算新的alphas[j]的值
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        #对新的alphas[j]进行阈值处理
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        #更新误差缓存
        updateEk(oS, j)
        #如果新旧值差很小，则不做处理跳出本次循环
        if (abs(oS.alphas[j] - alpahJold) < 0.00001): print("j not moving enough"); return 0
        #对i进行修改，修改量相同，但是方向相反
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alpahJold - oS.alphas[j])
        #更新误差缓存
        updateEk(oS, i)
        #更新常数项
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :]*oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alpahJold) * oS.X[i, :]*oS.X[j, :].T
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :]*oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alpahJold) * oS.X[j, :]*oS.X[j, :].T
        #谁在0到C之间，就听谁的，否则就取平均值
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[i]): oS.b = b2
        else: oS.b = (b1 + b2) / 2.0
        #成功返回1
        return 1
    #失败返回0
    else: return 0

def smoP(dataMatIn, classLabels, C, toler, maxIter):
    """
    Function：   完整SMO算法

    Input：      dataMatIn：数据集
                classLabels：类别标签
                C：常数C
                toler：容错率
                maxIter：最大的循环次数

    Output： b：常数项
                alphas：数据向量
    """ 
    #新建数据结构对象
    oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
    #初始化迭代次数
    iter = 0
    #初始化标志位
    entireSet = True; alphaPairsChanged = 0
    #终止条件：迭代次数超限、遍历整个集合都未对alpha进行修改
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        #根据标志位选择不同的遍历方式
        if entireSet:
            #遍历任意可能的alpha值
            for i in range(oS.m):
                #选择第二个alpha值，并在可能时对其进行优化处理
                alphaPairsChanged += innerL(i, oS)
                print("fullSet, iter: %d i: %d, pairs changed %d" % (iter, i, alphaPairsChanged))
            #迭代次数累加
            iter += 1
            print('--------------------',alphaPairsChanged)
        else:
            #得出所有的非边界alpha值
            #print('(oS.alphas.A > 0):',(oS.alphas.A > 0))
            #print('(oS.alphas.A < C):',(oS.alphas.A < C))
            #print('oS.alphas:',oS.alphas)
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            print('nonBoundIs:',nonBoundIs)
            #遍历所有的非边界alpha值
            for i in nonBoundIs:
                #选择第二个alpha值，并在可能时对其进行优化处理
                alphaPairsChanged += innerL(i, oS)
                print("non-bound, iter: %d i: %d, pairs changed %d" % (iter, i, alphaPairsChanged))
            #迭代次数累加
            iter += 1
        #在非边界循环和完整遍历之间进行切换
        if entireSet: entireSet = False
        elif (alphaPairsChanged == 0): entireSet =True
        print("iteration number: %d" % iter)
    #返回常数项和数据向量
    alphas_end = oS.alphas.getA()
    mylabel_end = array(classLabels)
    myDat_end = array(dataMatIn)
    w = (alphas_end*mylabel_end.reshape(-1,1)*myDat_end).sum(axis=0)
    return oS.b, oS.alphas,w

后记

真的好难啊，写了个啥啊，后面再从头学习一下重新编辑。

https://blog.csdn.net/weixin_42398658/article/details/83303061?utm_medium=distribute.pc_relevant.none-task-blog-baidujs-3
https://blog.csdn.net/luoshixian099/article/details/51227754