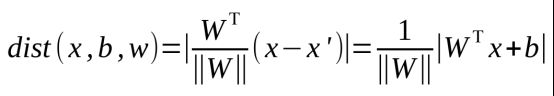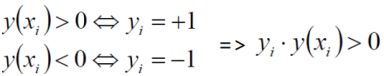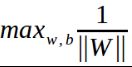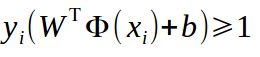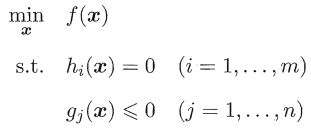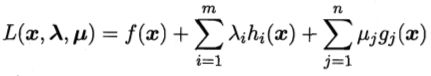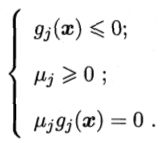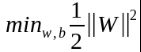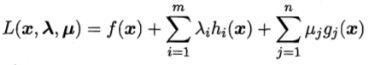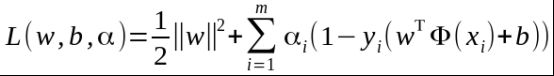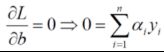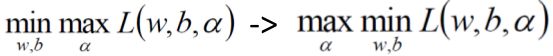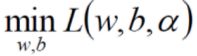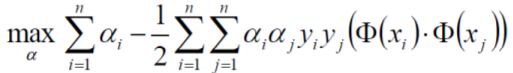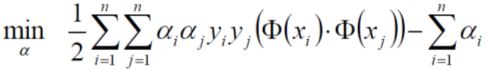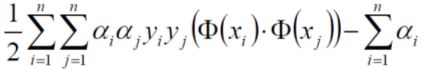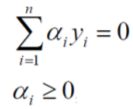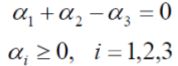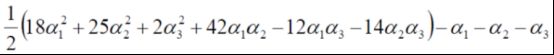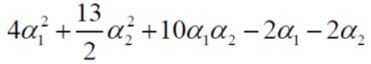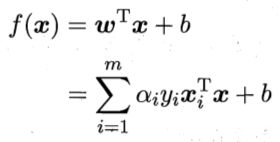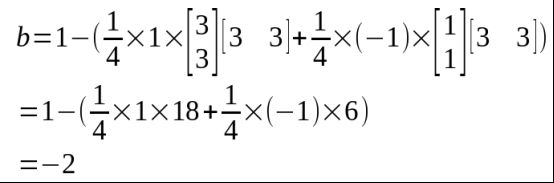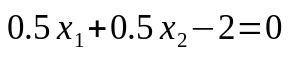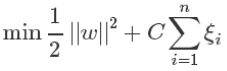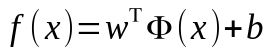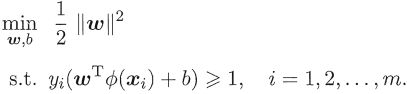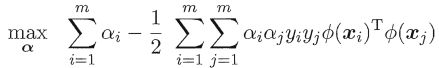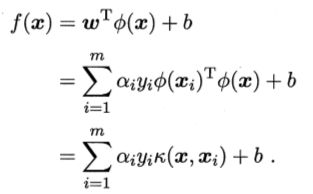机器学习入门（十）支持向量机
--------韦访 20181114
1、概述
继续学习，支持向量机在传统的机器学习的地位还是很高的，不过，现在风头已经被神经网络盖过了，但是，还是得学习的。
2、概念
先来看一下，为什么需要支持向量机？
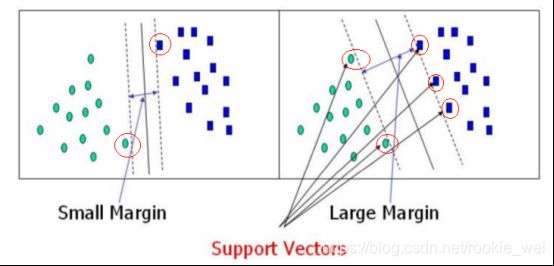
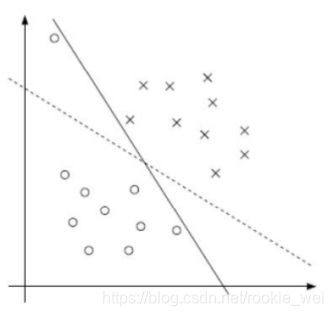
如上图所示，这是一个二分类问题，有三条直线，都能将红点和黄点分开，那么，哪条直线更优？
直观上看，中间的那条直线应该是最优的，因为另外两条直线都更接近样本的边界。用另一张图来更直观的看应该怎么求这条最优分界线。
如上图所示，左右两张图的直线都能将样本分类，直线旁边的两条虚线是与直线平行的，如果将两条虚线之间的距离看做容错率的话，显然右边那条直线的容错率是更好的，也就是更鲁棒，泛化能力更强。
3、距离公式
那这条直线应该怎么求呢？
既然远离样本边界的直线更好，是不是应该先找到离直线最近的样本，然后离它越远越好就行了？如上图所示，先找到离直线最近的样本点，然后，远离它。
这样我们就将问题转成了求“距离”的问题了。
在真实的分类任务中，样本可能不会刚好分布在二维平面上，有可能是多维的超平面上。在样本空间中，任何一个超平面都可以用如下方程表示，
WΤx+b=0
其中，W为法向量，决定超平面的方向，b为偏置项，决定超平面与原点之间的距离。
如上图所示，假设阴影部分的平面是我们的划分超平面，x是样本点，我们要求的就是x到划分超平面的距离。直接求距离可能不太好求，我们就间接来求。
在平面上随意找到两个点x`和x``，这两点组成一个向量，因为这两点在平面上，所以它满足公式，WΤx+b=0，分别将它们带入公式，得
WΤx`=-b, WΤx``=-b
因为法向量与x到平面距离的直线是平行的，所以，我们可以先求x到x`的距离d`，然后再求d`到法向量上的投影，就是我们要求的点x到平面上的距离了，距离公式如下，
4、数据标签定义
假设超平面能将训练样本正确的分类，则在数据集
中，yi为样本类别，若yi=+1，则有wΤxi+b>0，若yi=-1，则有wΤxi+b<0。如果我们将决策方程表示为，
则有，
将上面两式带入距离公式，得，
- 目标函数
对于决策方程(w, b)，可以通过缩放使得其结果值|y|≥1，为什么能这么缩放呢？上面的式子，
，让它左边和右边同时乘以一个值，等式还是成立的吧？那么总有一个值可以使得等式左边的大于1吧。带入，可以得到下式，
前面说过了，我们的目的是求离划分超平面最近的样本点，然后，远离它，那么，得到的目标函数应该如下，
由于
，所以，我们只需要考虑，
即可。
求极大值？我们以前的做法都是将它转变成求极小值的计算，求分数的极大值，不就是求分母的极小值吗？所以，可以将上式求极大值的问题转成下式，求极小值，
别忘了，上式成立还有一个约束条件，
上面两式就是支持向量机的基本型。
6、拉格朗日乘子法
在继续求解SVM之前，先来说说拉格朗日乘子法，拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法。通过引入拉格朗日乘子，可以将有d个变量与k个约束条件的最优化问题转化为具有d+k个变量的无约束优化问题求解。
等式约束g(x)=0优化问题：
假定x为d维向量，现在寻找x的某个取值x*，使得目标函数f(x)最小，且同时满足g(x)=0的约束条件。
从几何的角度看，这个问题的目标是在方程g(x)=0确定的d-1维曲面上寻找使得目标函数f(x)最小化的点。由此可得，
- 对于约束曲面上的任意点x，该点的梯度
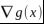正交于约束曲面。 - 在最优点x*，目标函数在该点的梯度
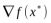正交于约束曲面。
如下图所示，
梯度
和
的方向必相同或者相反，则存在λ≠0，使得，
其中，λ称为拉格朗日乘子，拉格朗日函数如下，
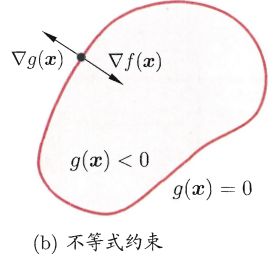
不等式约束g(x)≤0优化问题：
如上图所示，此时最优点x*在g(x)<0区域中，或者在g(x)=0边界上，
- 当x*在g(x)<0区域中，直接极小化f(x)即可。
- 当x*在g(x)=0上，则等价于上面的等式约束优化问题。需要注意的是，此时，
和
的方向必须相反，则存在常数λ>0使得
.
整合这两种情形，必须满足λg(x)=0，因此可以将在约束条件g(x)≤0下最小化f(x)，转化为在如下约束条件下，最小化拉格朗日函数
，
上面的条件称为KKT条件。
上面的做法可以推广到多个约束，假设有m个等式约束和n个不等式约束，且可行域D非空的优化问题，
引入拉格朗日乘子λ=(λ1,λ2...λm)Τ和μ=(μ1,μ2...μn)Τ，相应的拉格朗日函数为，
约束条件KKT为，
7、求解SVM
将
带入拉格朗日函数
得，
另
对w和b的偏导为0，
对w求偏导：
对b求偏导：
再将上面的式子带入原式，就可以将w和b消去，
由于对偶性质，
上面完成了第一步
，
现在我们继续对α求极大值，
求极大值，我们又可以将它转成求极小值，
别忘了上式成立是有条件的，
然后，解出α，根据下式再求出w和b，即可得到模型
8、求解SVM实例
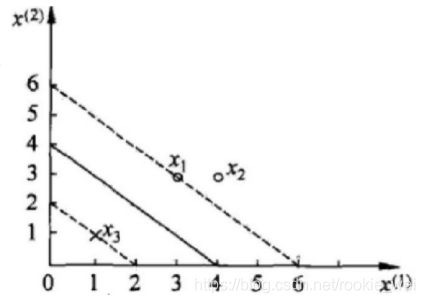
下面，用一个实例来看看怎么用上式对SVM求解。
如上图所示，我们有三个数据，其中，正例x1(3, 3)、x2(4, 3)，负例x3(1, 1)。
将这些数据带到式子，
其中，约束条件为，
因为我们已经有真实的数据了，所以，约束条件也就可以写成如下，
带入数据以后，原式子为，
又因为，
，所以可以将α3消去，上式简化为，
求极小值怎么办？求偏导呗，分别对α1和α2求偏导，令偏导等于0，可得，
因为用的是ubuntu自带的公式编辑软件，我不知道怎么编辑方程组，大家知道上面两式是方程组就好了，对上面方程组求解，得，
α1=1.5，α2=-1，这个结果并不满足我们的约束条件αi≥0，i=1,2,3
所以我们的解应该是在边界上，分别令α1和α2等于0，带入，得，
α1=0，α2=-2/13
α1=0.25，α2=0
上面两个结果中，第一个结果因为α2<0，还是不符合约束条件，而第二个结果刚好符合约束条件。又因为
所以，结果为α1=0.25，α2=0，α3=0.25 ，所以最小值在(0.25, 0, 0.25)处。
然后，将上面α的值带入下面式子，求解w，
，得
得到w后，再根据下式求出b，
将x1的数据带入上式，得，
所以，最后得到的平面方程为，
有没有发现，在上面这个例子中，我们最终得到的模型方程其实跟点x2(4,3)没有关系，也就是说，如果求得的αi=0，则该样本对f(x)没有任何影响。也就是真正发挥作用的样本，是α不为0的样本点。
9、松弛因子
如上图所示，有时候数据中存在一些噪音点，如果我们也将它们考虑进去了，可能得到的线就不太好了。这是因为我们的方法要求把两个类别完全分开，这时候我们可以适当的放松要求，引入松弛因子来解决这个问题。
所以我们新的目标函数变成了这样，
当C很大时，意味着分类严格
当C很小时，意味着有更大的错误容忍度
C是我们要指定的一个参数。
10、核函数
现实任务中，样本空间内可能不存在一个能正确划分两类样本的超平面，对于这样的问题，我们可以将原始的样本空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分，如下图所示。
如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。
我们令Φ(x)表示将x映射后的特征向量，于是，在特征空间中划分超平面所对应的模型可表示为，
其中，w和b是模型参数，跟上面讲的一样，于是有，
其对偶问题是，
约束条件为，
上式中，涉及到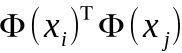
的计算，这是样本xi和xj映射到特征空间后的内积，因为特征空间的维数很高，甚至是无穷维，所以，直接计算的难道非常大，为避开这个障碍，设想有这样一个函数，
即xi和xj在特征空间的内积是它们在原始样本空间中通过函数k(.,.)计算的结果。于是，重写式子为，
求解后得，
其中，函数k(.,.)就是核函数。
核函数定理：令x为输入空间，函数k(.,.)是定义在x×x上的对称函数，则k是核函数当且仅当对于任意数据D={x1,x2,,,xm}，核矩阵K总是半正定的。
上面定理表明，只要一个对称函数所对应的核矩阵是半正定，它就能作为核函数使用。
上面的定理是什么鬼，不是我们研究的重点，下面列出常用核函数，
此外，核函数还可以通过函数组合得到，例如，
- 若k1和k2是核函数，则对于任意整数r1、r2，其线性组合r1k1+r2k2也是核函数
- 若k1和k2是核函数，则核函数的直积
也是核函数。
3、若k1为核函数，则对于任意函数g(x)，
也是核函数。
如果您感觉本篇博客对您有帮助，请打开支付宝，领个红包支持一下，祝您扫到99元，谢谢～～
