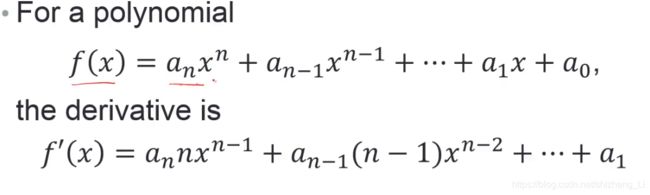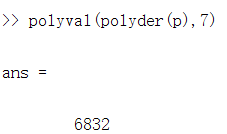台湾国立大学郭彦甫Matlab教程笔记(14)polynomial differentiation多项式微分
台湾国立大学郭彦甫Matlab教程笔记(14)
today:
polynomial differentiation and integration多项式微分与积分
numerical differentiation and integration数值微分与积分
Differentiation微分
1.the derivative of a function f(x) is written as
notation as follow

2.the rate of the change in the function f(x) with respect to x函数的变化率随着自变量x的变化而变化
3geometrically , f’(x0) represents the coefficient of the line tangent to the curve in the point x0
Polynomial Differentiation多项式微分
MATLAB中多项式如何表示?
representing Polynomials in MATLAB
1.polynomials were represented as row vectors作为一个行向量
举例:
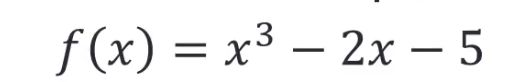
to enter this polynomial into MATLAB ,use
p=[1,0, -2,-5];
我们关注的是多项式的系数。把系数排列成向量。
如何显示一个多项式的数值?
values of polynomials: polyval()
举例:

这个多项式在matlab绘制出来的结果如下:
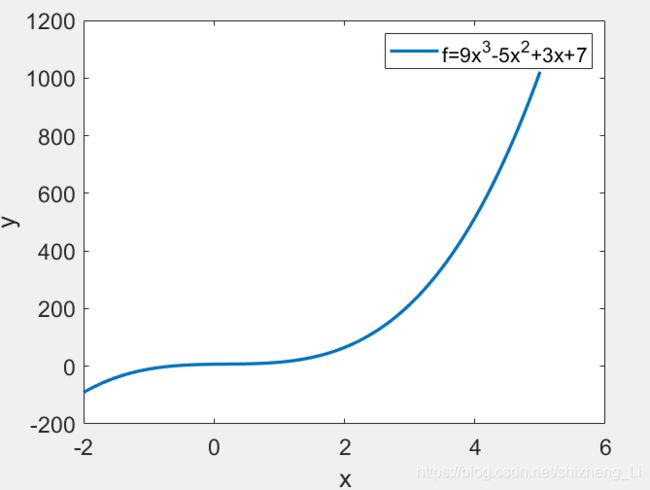
例程:
a=[9,-5,3,7];%多项式的系数
x=-2:0.01:5;%定义域
f=polyval(a,x);%第一个参数是多项式的系数,第二个是自变量
plot(x,f,'linewidth',2);%画线+线宽设置
xlabel('x');ylabel('y');%坐标轴
set(gca,'fontsize',14);%设置字体
legend("f=9x^3-5x^2+3x+7");%函数名称
这个polyval函数的使用:f=polyval(a,x);%第一个参数是多项式的系数,第二个是自变量,a是一个向量,x是定义域。
多项式的微分
polynomial differentiation :polyder()
举例:
给定下图的一元四次多项式,求它的导数(derivative)

解决:
首先表示出来这个polinomial p=[5 0 -2 0 1]
接着计算微分 polyder§这个polyder怎么用呢?直接把多项式的系数向量传进来即可。
代码:
p=[5 0 -2 0 1];
polyder(p)
运行结果:
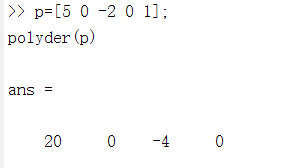
可以看出,用matlab求微分,给出的是一个向量
![]()
求某一点的导数的值
需要使用polyval函数:第一个参数是多项式的系数,这里的多项式变成了导函数,第二个参数是具体的数值,自变量的值。
polyval(polyder(p),7);
下面是作业题:
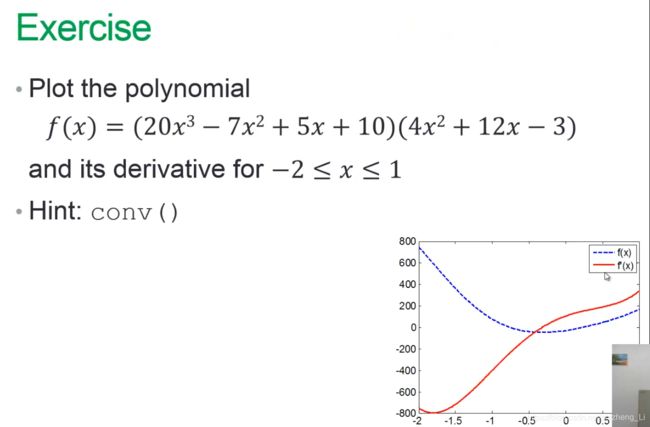
题目:画出下面多项式的图形和它的导数的图形。
给出的是一个相乘的形式,老师给的提示是用conv这个函数
下面是笔者找到的关于conv的官方文档
关于conv的用法,下面截取多项式乘法这一部分,可以看出conv函数传出来的就是一个向量,这个向量是两个多项式相乘之后的多项式的系数。所以,我们知道如何求这个多项式的系数了
a=[20 -7 5 10];%第一个多项式相乘之前
b=[4 12 -3];%第二个多项式相乘之前
x=-2:0.01:1;%自变量范围
A=conv(a,b);%计算相乘之后多项式的系数
f=polyval(A,x);%多项式的值
%求导数
A1=polyder(A);%得到的是导数的系数
f1=polyval(A1,x);%得到多项式的值
%绘制多项式
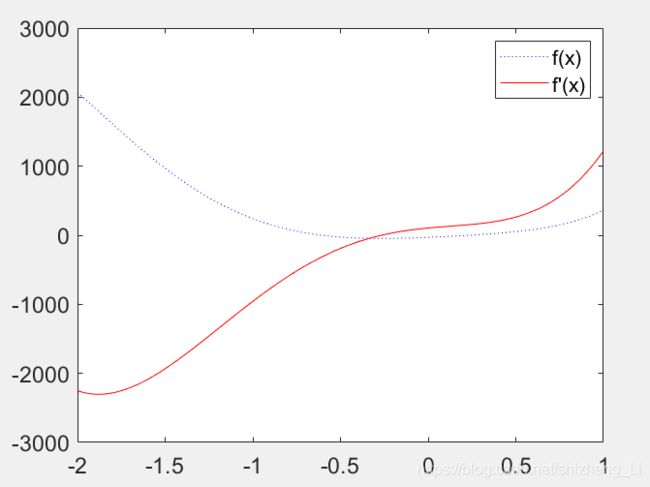
plot(x,f,'b:',x,f1,'r-');
legend('f(x)','f''(x)');%函数标头
set(gca,'fontsize',14);%设置字体
运行结果:
【总结】
这篇文章介绍了matlab中计算多项式微分的几个函数。包括:polyval()和polyder()
还有conv()多项式乘法