数据预处理(三)数据变换
文章目录
- 数据变换
- 一、特征二值化
- 二、特征归一化
- (一)、总和标准化
- (二)、标准差标准化
- (三)、极大值标准化
- (四)、极差标准化(区间放缩法,0-1标准化)
- 三、连续特征变换
- 四、定性特征哑编码:One-hot编码
数据变换
数据变换即对数据进行规范化处理,以便于后续的信息挖掘。常见的数据变换包括:特征二值化、特征归一化、连续特征变化,定性特征哑编码等。
一、特征二值化
特征二值化的核心在于设定一个阈值,将特征与该阈值比较后,转话为0或1(只考虑某个特征出现与否,不考虑出现次数,程度),它的目的是将连续数值细粒度的度量转化为粗粒度的度量。
下面为Python实现特征二值化的方法:
from sklearn.preprocessing import Binarizer
import numpy as np
data = [[1,2,4],[1,2,6],[3,2,2],[4,3,8]]
binar = Binarizer(threshold=3) #设置阈值为3,<=3标记为0,>3标记为1
print(binar.fit_transform(data))
#fit_transform(X)中的参数X只能是矩阵
print(binar.fit_transform(np.matrix(data[0])))
二、特征归一化
特征归一化也叫做数据无量纲化,主要包括:总和标准化、标准差标准化、极大值标准化、极差标准化。这里需要说明的是,基于树的方法是不需要进行特征归一化的,例如GBDT,bagging、boosting等等,而基于参数的模型或基于距离的模型,则都需要进行特征归一化。
(一)、总和标准化
总和标准化处理后的数据介于(0,1)之间,并且它们的和为1。总和标准化的步骤和公式也非常简单:分别求出各聚类要素所定义的数据的总和,以各要素的数据除以该要素的数据总和,即:
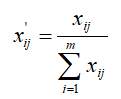
经过总和标准化处理后所得的新数据满足:
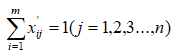
(二)、标准差标准化
标准差标准化公式如下:
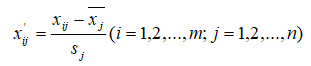
其中
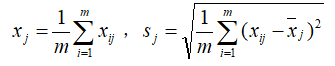
标准差标准化处理后所得到的新数据,各要素(指标)的平均值0,标准差为1,即:

(三)、极大值标准化
结果极大值标准化的公式如下所示:
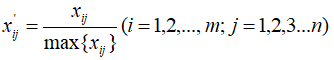
极大值标准化后的新数据,各要素的最大值为1,其余各项都小于1。
对稀疏数据进行中心化会破坏稀疏数据的结构,这样做没有什么意义,但可以对稀疏数据标准化,极大值标准化就是为稀疏数据设计的,同时这也是一种常用的方法,Python中极大值标准化为MaxAbsScaler(),如果要使用Python中标准差标准化(StandardScaler)则需要设置with_centering = False,否则将破坏数据稀疏性。
(四)、极差标准化(区间放缩法,0-1标准化)
极差标准化的计算公式如下:
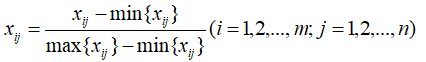
经过极差标准化处理后的新数据,各要素的极大值为1,极小值为0,其余数值均在0与1之间。这里的min{x_ij}和max{x_ij}指的是和x_ij同一列的最小值和最大值。
如果数据中有离群点,对数据进行均值和方差的标准化效果并不好,这时候可以使用robust_scale和RobustScaler作为代替,它们有对数据中心化和数据的缩放鲁棒性更强的参数。
三、连续特征变换
连续特征变换的常用方法有三种:基于多项式的数据变换、基于指数函数的数据变换、基于对数函数的数据变换。连续特征变换能够增加数据的非线性特征捕获特征之间的关系,有效提高模型的复杂度。
#encoding=utf-8
"""
生成多项式特征与自定义函数(如:log等)
在输入特征中增加非线性特征可以有效提高模型的复杂度,其中最常用的是多项式特征
matrix =
[[0 1 2]
[3 4 5]
[6 7 8]]
当degree = 2时,以第二行为例:
[1 3 4 5 3*3 3*4 3*5 4*4 4*5 5*5]
当degree = 3时,以第二行为例::
[1 3 4 5 3*3 3*4 3*5 4*4 4*5 5*5 3*3*3 3*3*4 3*3*5 4*4*3 4*3*5 5*5*3 4*4*4 4*4*5 4*5*5 5*5*5]
"""
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import FunctionTransformer
"""生成多项式"""
X = np.arange(9).reshape(3,3)
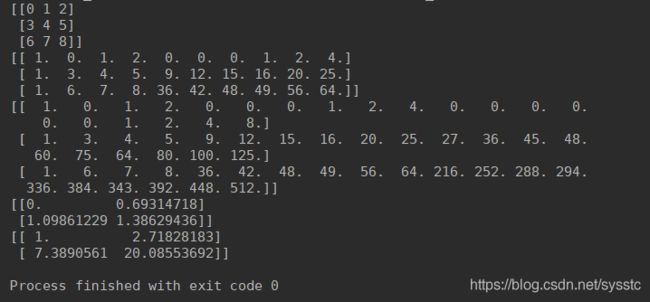
print(X)
ploy = PolynomialFeatures(2)
print(ploy.fit_transform(X))
ploy = PolynomialFeatures(3)
print(ploy.fit_transform(X))
"""自定义转换器"""
X = np.array([[0,1],[2,3]])
transformer = FunctionTransformer(np.log1p) #括号内的就是自定义函数
print(transformer.fit_transform(X))
transformer = FunctionTransformer(np.exp)
print(transformer.fit_transform(X))
四、定性特征哑编码:One-hot编码
one-hot编码又称为独热码,即一位代表一种状态,及其信息中,对于离散特征,有多少个状态就有多少个位,且只有该状态所在位为1,其他位都为0。
举例来说:
天气有:{多云、下雨、晴天}三种情况,如果我们将“多云”表达为0,“下雨”表达为1,“晴天”表达为2,这样会有什么问题呢?
我们发现不同状态对应的数值是不同的,那么在训练的过程中就会影响模型的训练效果,明明是同一个特征在样本中的权重却会发生了变化。
那么,如何对这三个值进行one-hot编码呢?这时候我们就使用到one-hot编码,
即对于:
天气:{多云、下雨、晴天}
湿度:{偏高、正常、偏低}
当输入{天气:多云,湿度:偏低}时进行独热编码,天气状态编码可以得到{100},湿度状态编码可以得到{001},那么二者连起来就是最后的独热编码{100001}。此时{0,2}转换后的长度就是6 = 3+3,即{100001}。
sklearn中有封装好的独热编码:OneHotEncoder
from sklearn.preprocessing import OneHotEncoder
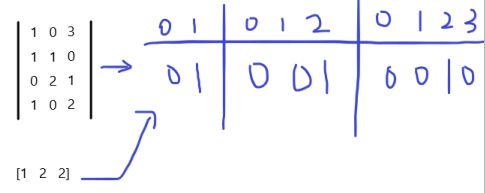
data = [[1,0,3],[1,1,0],[0,2,1],[1,0,2]]
oneHotEn = OneHotEncoder()
print(oneHotEn.fit(data))
print(oneHotEn.transform([[1,2,2]]).toarray())
print(oneHotEn.n_values_) #不同特征对应的值有几种
print(oneHotEn.feature_indices_) #不同特征对应的索引号
输出:

代码分析:
data是一个矩阵,一列代表一个特征,可知矩阵有3个特征,且第一个特征有2个特征值(0,1),第二个特征有3个特征值(0,1,2),第三个特征有4个特征值(0,1,2,3)。当输入[1,2,2]时,相当于第一个特征,特征值为1的位标记为1,第二个特征,特征值为2的位标记为1,第三个特征,特征值为2的位标记为1。
将离散特征进行one-hot编码后,距离计算就会更加合理。