机器学习(5)——贝叶斯学习(二)
在上一节的分析中,我们的讨论基本上都是以一个输入变量来讨论,但是在实际的情况中,存在不止一个输入变量,那么我们如何从多个不同量和观察来推导概率呢?这一章中我们将基于这个问题来进行相关的讨论。
在开始之前,先介绍一个概念——贝叶斯网络(Bayesian Networks),它能够很好的在复杂空间表示和操作概率量。
一:联合分布(Joint Distribution)
1.1条件独立性
这里我先用一段英文的描述来讲解一些什么是条件独立性:
X is conditionally independent of Y given Z if the probability distribution governing X is independent of the value of Y given Z the value of Z; that is it. We call it conditional independent(条件独立).
我们这里在使用一句公式来描述这个特征:
说的通俗一点就是 X 发生的概率与 Y 无关。
这里我们在使用另外一种方式来证明一下:
因为条件独立,我们可以得到如下的公式:
根据概率论的链式法则,我们得到如下的公式:
结合上边的公式我们可以得到:
这样就又一次的验证了我们说的那句话。
但是在现实生活中,特别是在机器学习这方面,我们如果要运用到这个条件独立的特性,即找到两个条件独立的属性,是非常困难的,但是我们做了相应的转变,将其转变为在满足Z的条件下,找到条件独立的两个属性——X,Y,这种相对就容易多了。(具体为什么会这样,笔者没有具体的研究过,因为笔者觉得这是哪些科学家干的事情,如果我们只是简单的使用的话,在初期,是没有精力去研究这个东西的)。
1.2联合分布
这里我们列出了如下的一个场景:
| Lightning | Storm | Probability |
|---|---|---|
| T | T | 0.25 |
| T | F | 0.40 |
| F | T | 0.05 |
| F | F | 0.30 |
上边是一个关于闪电和打雷发生的概率表。
这里我们只列出的两个属性Lightning、Storm。在我们讨论的这个过程中,这两个事件发生是不相关的(有些人说,打雷和暴风雨是相关的,但是这个要注意,你们说的相关是指物理上的相关性,而我们这里讨论的是统计相关性,所以他们是条件独立的两个事件)。基于我们前边讨论的概率的相关公式,我们可以得出求出发生闪电的概率和发生风暴的概率分别是多少。
但是这里我们思考一下,如果我们继续添加属性的话,会发生社么样的事情?我们需要考虑的情况越来越多,非常不利于分析。如果我们仍然添加的是这种只有发生和不发生的条件的话,那我们的所需要考虑的情况就得满足 2n 。这将非常不利于我们的分析。那么这里我们就要运用到另外一个概念了——因式分解。
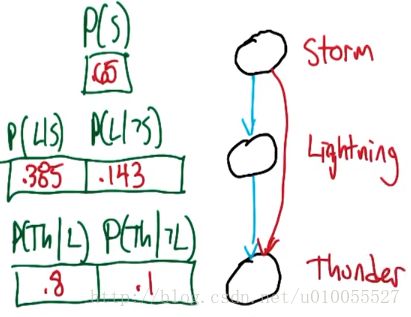
这里我们基于前边的场景,添加一种属性——thunder。由于情况比较多,这里不用表格的形式来分析,我们用一张图来描述我们的情况:

这里我们先列出如下的一个公式:
这个公式是一个代表性的公式:公式左边的含义是——在发生暴风雨的情况下,打雷但是没有闪电的概率;公式右边的含义是——没有发生暴风雨的情况下,打雷但是没有发生闪电的情况。这里我们是不是可以得出——打雷、闪电的发生与暴风雨无关呢?如果你不相信的话,你可以计算下其它的情况,你会发现这个情况是属实的。
请看左边,我们将事件分成不同的层级去考虑。图中右边的子图,被我们称为信念网络(Belief Network)。理解这个图形的时候,一定要注意,这里的箭头并不代表因果关系,即:暴风雨导致了闪电、闪电导致了打雷。箭头只是表示统计相关性,与它们背后实际发生的过程并没有任何的关系(这个可能对于大部人来说可能会下意识的会产生这种想法,所以这里特别说明一下),这个我们在前边已经提到过。
特别说明:在信念网络(Belief Network)中箭头只是表示相关性,而这个相关性是统计相关性。也可以表示条件独立性。
1.3 从联合分布中取样
如果我们按照如图所示的信念网络进行取样的话,我们应该满足什么情况呢?正确的取样顺序就是右侧中从上到下所示。那么针对这种图形我们取样的标准是什么呢?——拓扑关系,这种是处理图形的标准做法之一,他的运算非常的快,但是它需要依赖某种特性。1:它必须是一个有向无环图。
这里我们在讨论一下联合分布的个概率:
我们来分析一下这个过程中我们需要考虑的情况:1:我们可以从联合分布的节点出发,指定每个节点的概率,即所谓的条件概率表。2:我们也可以从每个节点的条件概率表的值出发,计算我们想要的任何组合,任何变量联合组合的概率。就如上边公式的左右两边,分别对应两种不同的情况——变量的某些分配联合概率等于所有单个值的乘积。
标注一下,这里我们需要进一步的讨论一下关于种类的问题,笔者暂时正在研究,线性跳过。
为什么从联合分布中取样是一个好主意?
- 因为他是分布的两个用途之一:通过给定一个值,我们可以告知这个值发生的概率,就像概率函数一样;如果你有一个不错的分布,我们可以根据这个分布生成值。
- 如果分布能够代表某个过程的话,我们能够通过机器来模拟这个过程。
- 近似推理:如果我们知道一个分布,我们可以根据这个分布推断出每个事件的概率,就如前边讲到的求 P(Storm) 的问题;我们同时可以做出一些其他类似的推理。以前边的打雷为例:我们想知道同时发生打雷和闪电的概率?同时发生暴风雨和打雷的概率?等等。这个是针对机器来说的。
- 图形化。这样我们就可以以一个更加直观的方式来感受这个分布。这一部分实际上是从人的角度得出的结论,因为从本质上讲的话,它实际还是第三点中说的近似推理。
1.4 推理规则(Inferencing Rule)
边缘化(Marginalization)规则,我们可以通过对一些其它变量求和,然后求出它们的联合概率:
为了帮助大家理解这个规则,我们这里展示一张图:

边缘化规则讲的是,如果我们要求 x 的概率,那么我们分解它,将世界分解成 x 和 非y ,加上x和y的地方。那么 x 的概率就是: y为假时,x的概率和y为真实,x的概率 。
链式规则(Chain Rule):
关于链式规则我们要说明一点:当两个事件条件独立的时候,我们可以将 P(y|x) 简化为 P(y) 。为了加深理解,请看下图:
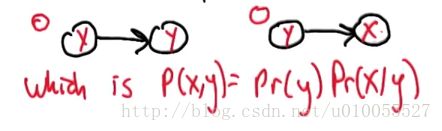
上图上提出了一个问题,就是什么时候 P(x,y)=P(y)P(x|y) 。正确的答案是第二个(即右边的哪一个),因为左边的哪一个, x 的发生是与 y 没有关系的。
贝叶斯规则(Bayes Rule):
这个已经在前边讲解到了,不再做进一步的说明。
二:朴素贝叶斯
2.1手工推理
2.2朴素贝叶斯(Naive Bayes Rule)
我们在上一节中,通过相关的公式完成了对应概率的推导,但是在计算机中我们怎么实现着一个过程呢?