Logistic Regression及python实现

本文所有代码都是基于python3.6的，数据及源码下载：传送门

引言

本次分享，我们将介绍一个经典的二分类算法——逻辑回归。逻辑回归虽然不在十大数据挖掘算法之列，但是这个算法是机器学习从统计学领域借鉴的一种算法，其算法最经典之处是使用到了最优化算法。关于线性回归与逻辑回归的详细介绍与数学推导，在我前面翻译的CS229讲义里都有提到：CS229 Lecture Note 1(监督学习、线性回归)、 CS229 Part2 分类与逻辑回归。此处就不做详细介绍了。
利用逻辑回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。这里的“回归”一词源于最佳拟合，表示要找到最佳拟合参数，使用的是最优化算法。

逻辑函数

逻辑回归，需要一个函数能接受所有的输入然后预测出类别。于是就有了逻辑函数，逻辑函数又叫Sigmoid函数，是统计学家为了描述生态学中人口增长特性，提出的一种方法。Sigmoid函数是一个S形状的曲线，能够接受任意实数并将其映射到近似0，1处。图形如下如所示：

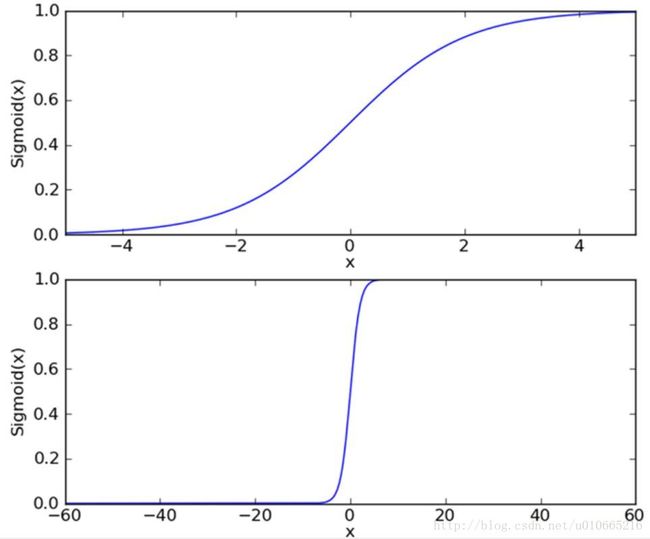
公式如下所示：

σ(z)=11+e−z

确定了分类函数为Sigmoid函数后，接下来我们我们就需要确定逻辑回归的第二部分了“回归系数”——即最佳拟合参数。

基于优化方法的最佳回归系数的确定

前面我们提到了分类函数Sigmoid能够将任意实数输入映射到0，1上。那么我们需要确定的是，这个任意实数输入，该如何表示呢？根据CS229里面的说明，我们利用一个线性函数表示，将Sigmoid函数的输入记为z，z由下面的公式给出：

z=w0x0+w1x1+w2x2+...+wnxn

采用向量的写法，上述公式就可以写成 z=wTx 。

梯度上升法

这里我们使用的第一个优化算法是梯度上升算法。如果大家看了我前面翻译的讲义的话，看到这里不免会心生疑问，为什么在讲线性回归时，使用的是梯度下降算法，但是在讲逻辑回归时使用的就是梯度上升算法了。首先我们需要明确的一点是，梯度上升算法求得是函数的最大值，梯度下降算法求得是函数的最小值。在线性回归中，我们的目标函数是最小二乘：

；而逻辑回归中，我们的目标函数是似然函数:

很明显，最小化最小二乘与最大化似然函数本质上是等价的。具体推导大家可以去看CS229讲义。那么这里我们的梯度上升算法的迭代公式如下所示：

w:=w+α∇wf(w)

这个公式将一直被迭代执行，直到达到某个停止条件为止，比如说迭代次数达到某个指定值或算法达到某个可以允许的误差范围内。

利用梯度上升找到最佳参数

我们来看一个逻辑回归分类器的应用例子。采用的数据集如下图所示：

梯度上升的伪代码如下所示：

代码如下：

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)             #convert to NumPy matrix
    labelMat = mat(classLabels).transpose() #convert to NumPy matrix
    m,n = shape(dataMatrix)
    alpha = 0.001                           #alpha固定默认设为0.001相当于learning rate
    maxCycles = 500                         #迭代结束条件
    weights = ones((n,1))
    for k in range(maxCycles):              #heavy on matrix operations
        h = sigmoid(dataMatrix*weights)     #matrix mult
        error = (labelMat - h)              #vector subtraction
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
    return weights

分析数据，可视化

我们利用梯度上升算法，求到最佳回归系数，然后将回归方程即决策边界可视化出来，如下所示：

从图上可以看出分类的效果不错。但是众所周知在实际应用中，梯度上升算法又叫作批量梯度上升，因此在每次迭代更新的过程中都是加载整个数组进行计算，所以当数据量很大时，这个计算量就真的大了。因为为了优化这个算法，有人提出了一个解决方法：一次仅用一个样本点来更新回归系数。这个方法被称为随机梯度上升法，与上面普通批量梯度上升算法对应的是这个算法是在线学习算法，可以在新样本来临时对分类器进行增量式更新。

随机梯度上升算法

伪代码如下图所示：

随机梯度上升算法的代码如下所示：

def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)   #initialize to all ones
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

分析数据，可视化

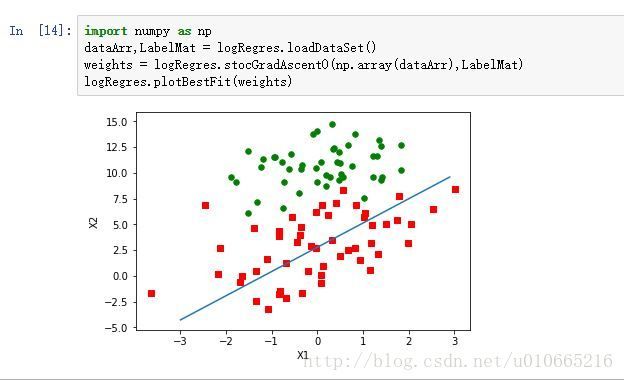
大家会发现，效果并不是很好，虽然说这里只遍历了一次数据集。这里我们将数据集也遍历500次看看具体效果：

如上图所示，这个效果看起来与上面的批量处理没什么差别，很明显从数学角度看，计算量都是一样的，并没有体现随机梯度上升算法的优异性。
大家看了这个代码可能也会有疑问了，不是说是随机梯度上升么，那么这个代码里的“随机性”在哪里体现呢？

随机梯度上升改进版

在实际应用中，通过每次迭代调整alpha来缓解数据高频波动。并且通过随机选取样本来更新回归系数，减少周期性波动。
实际代码如下所示：

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)   #initialize to all ones
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not 
            randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

分析数据，可视化

分类效果如图：

这样分类效果不仅和批量处理差不多，而且收敛速度更快，迭代次数更少！

总结

逻辑回归算法的目的是寻找一个非线性函数Sigmoid的最佳拟合参数，在求解过程中用最优化算法完成。这个算法本质上是一个线性回归，或者是特殊的线性回归。所以处理不好一些特征相关的应用场景。逻辑回归在一些推荐场景中有些应用，但是效果一般吧，但是逻辑回归简单快速，而且背后的概率原理经得起推敲，所以还是很受欢迎的。