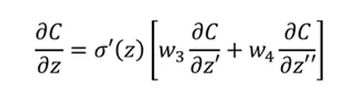李宏毅机器学习笔记(8):backpropagation
0 引言
回顾一下之前学习过的,在求解神经网络时,我们通常使用梯度下降算法进行求解。
首先,先自定义一组参数作为我们的起始值,之后计算我们需要使用的梯度,有了梯度之后就可以利用它进行迭代求解了,如图0-1。
显而易见的是,在一个神经网络中,可能参数数目成千上万,远超过我们的想象,那么这么庞大的计算量,我们就需要一些可以辅助我们的工具。backpropagation(反向传播)可以帮助我们有效的进行渐变迭代计算。
图0-1 梯度下降
1 复合函数求导法则
bp并不需要我们掌握特别强大的数学功底,只需要我们掌握高数中很基本的链式求导法则就行了,这里简要介绍复习。
图1-1介绍了链式求导法则最基本的知识:
- 第一种情况下,一元复合函数求导,内部求导与外部求导的乘积。
- 第二种情况下,多元复合函数求导,划分求导路径,不同路径求导后加和就行了。
图1-1 复合函数求导法则
2 backpropagation
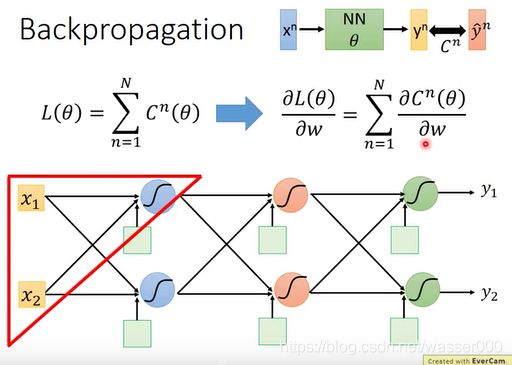
在计算损失函数函数的时候,总的损失函数可以写成每一个训练样本所构成的损失函数之和。而每一个样本所构成的损失函数为这个样本经模型输出后,模型的预测值与样本实际值之间的差距。不管是交叉熵还是均方误差都是在衡量这个差距。
那么为了分析总的损失函数,对总的损失函数求导,我们可以对每个样本的损失函数进行求导进行分析,之后进行求和分析就行了。如图2-1,先对图中红色三角形的一个小的逻辑回归进行分析。
图2-1 分析(1)
对一个逻辑回归进行分析,每个逻辑回归先进行一个线性的运算过程,在进行一个sigmoid函数处理过程,当然激活函数也是可以选择其他激活函数的。
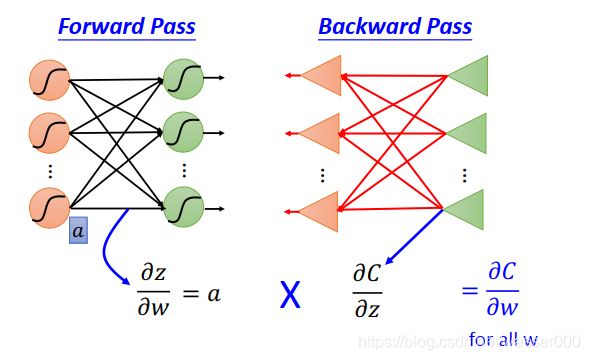
那么对损失函数求导就可以拆成两项分布求导的积,如图2-2,一项是损失函数对z求导(z为逻辑回归中的线性方程),一项是z对我们需要梯度下降的参数w的求导。
z对w求导称为前向传播,损失函数对z求导称为反向传播。
图2-2 分析(2)
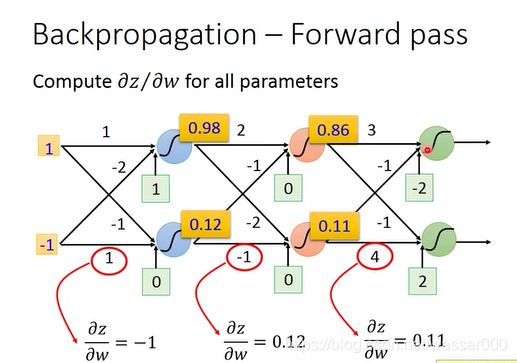
对于前向传播,不用算就能看出来:
那么我们就能够很容易理解前向传播了,对于前向传播中的偏微分,这个值应该是上一级的输出值,这也代表了前向传播中某一个参数的权重。
图2-3 前向传播
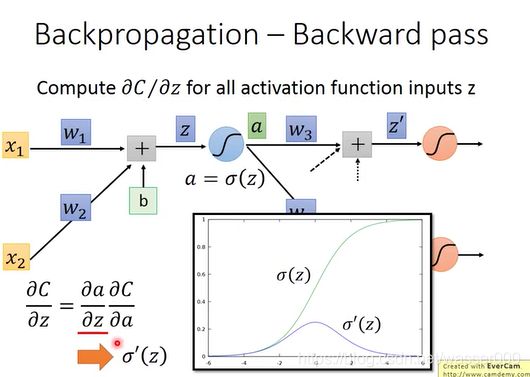
接下来对反向传播进行求解分析,如图2-4。从这一节神经元向之后的神经元看过去,对z需要进行一个激活函数的运算(这个例子假设是sigmoid函数),后作为下一级的输入。那我们的反向传播的偏微分就可以写成图2-4中的相乘的形式,由损失函数对激活函数偏导乘激活函数对z偏导。
图2-4 反向传播(1)
激活函数对z偏导是一个比较好求解的,如图2-4,就是σ(z)![]() 函数的偏导。
函数的偏导。
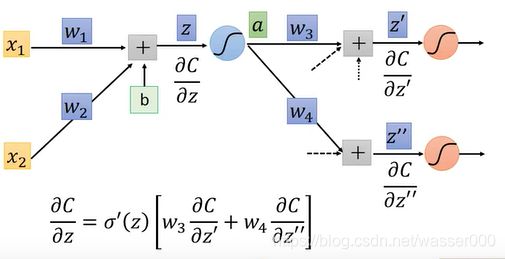
那么另一部分怎么求解呢?假设我们这个模型是下一级只连接了两个神经元(更多神经元如果理解这个后也就明白了),那么我们的输出结果就会对之后的两个神经元产生影响,那么我们可以用求导的链式法则去表示出上一步我们需要求解的部分,如图2-5。我们发现图中?的两个部分还是没有求解出来,这个下文会接着说。
图2-5 反向传播(2)
表示出的结果如下图2-6:
图2-6 结果
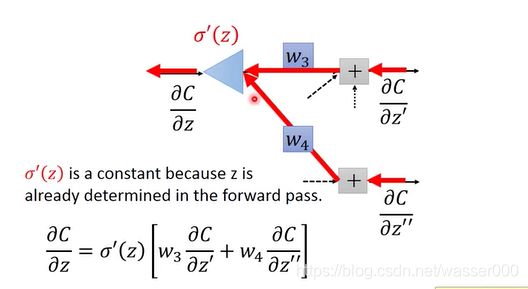
换一种思路去更好的理解反向传播,如图2-7。可以看成是一个新的网络,这个网络是和我们刚才的网络输入输出是相反的。这个网络输入了下图中的偏导数,经过上文中介绍的处理方式,得到了之前一级的偏导数,这就是一种反向传播。
而对于σ(z)![]() 函数的偏导,z在输入的时候就已经确定了具体的大小,所以σ(z)
函数的偏导,z在输入的时候就已经确定了具体的大小,所以σ(z)![]() 函数的偏导也就是确定的常数了。
函数的偏导也就是确定的常数了。
图2-7 反向传播
3 最后部分的计算
还记着上文中两个没有被计算的红色?部分嘛,这一部分中将提及这个的处理方式。
分为两个情况去处理这部分的计算:
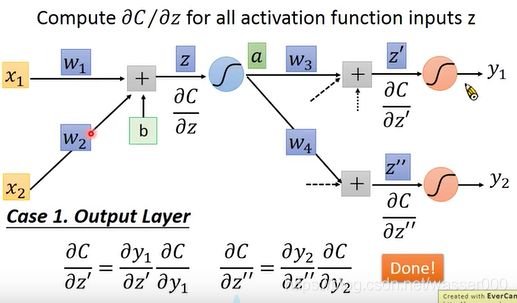
情况1 下一层为输出层
如图3-1,当下一层为输出层的时候,由于我们在输入样本时是可以计算出输出值y1![]() 和y2
和y2![]() 的。所以这部分的偏导数也是可以很容易做出来的。
的。所以这部分的偏导数也是可以很容易做出来的。
图3-1 计算情况1
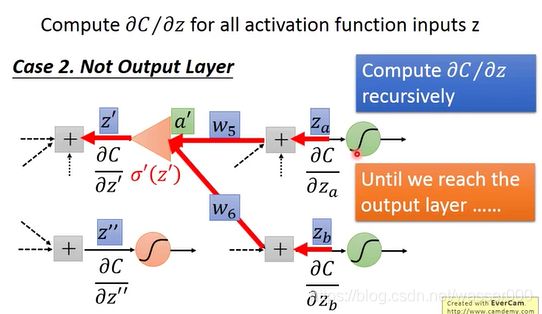
情况2 下一层并不是输出层
这种情况下,我们很容易想到,如果知道下一层的微分值,那么不是可以很容易求解出这一层的微分值嘛?
这时大家肯定想到了递归的思想,不断的递归就可以推到输出层从而计算出我们想要的结果。
图3-2 计算情况2
通常为了简化计算,我们会新建一个新的网络,这个网络和我们要求解的网络输入输出相反,如图3-3。
图3-3 反向传播
4 总结
最后在这个部分总结下bp,bp是为了简化对神经网络做梯度下降时带来的运算量巨大的问题。bp主要分为反向传播和前向传播。
前向传播很容易,主要传播的就是神经网络的输入。这个每一级的输入都会作为我们的偏导数来供我们去做梯度下降。
反向传播传播的是损失函数对z的偏导(z是每一级线性方程的输出),这个偏导数可以通过,从输出层到输入层的反向求解,使得运算达到进一步的简化。
图4-1 bp总结
bp这个部分算是一个比较难以初步学习就能深刻理解的部分,他对数学功底要求不是很高,使用的就是简单的链式求导法则和递归思想,这里建议去看下李宏毅老师或者吴恩达老师的视频,可以多多理解下。
当然这部分如果听不懂是不影响我们使用神经网络的。