特征多项式、代数重数与几何重数

概要

主要介绍了特征多项式、代数重数、几何重数以及重要的性质。
 

---

一个复方阵有多少个特征值？

首先要做的当然是给出定义啦！

接下来给出一个结论：

  证明：我们分三步加以说明，

1. 由 \(tI-A\) 行列式的计算展开表达式知，只有全取对角元素时，求和项次数才能达到 \(n\)，即
   \begin{align}
   (t-a_{11})\cdots(t-a_{nn})=t^n-(a_{11}+\cdots+a_{nn})t^{n-1}+\cdots
   \label{eq1}
   \end{align}
   任何其它因子必包含非对角因子 \(-a_{ij}\,(i \neq j)\)，则对角元素 \(t-a_{ii}\) 与 \(t-a_{jj}\) 不可能也是因子。因此求和项次数不可能大于 \(n-2\)，于是式 \ref{eq1} 确定了 \(t^n\) 和 \(t^{n-1}\) 的系数。\(p_A(t)\) 的常系数项正好是 \(p_A(0)=\mathrm{det}(-A)=(-1)^n \mathrm{det} A\) .
2. $p_A(\lambda)=0 \Leftrightarrow \mathrm{det}(\lambda I-A)=0 \Leftrightarrow (\lambda I-A)x=0, x\neq 0 \Leftrightarrow \lambda \in \sigma(A) $
3. 一次数为 \(n\geqslant 1\) 的多项式至多有 \(n\) 个不同零点。

 
结论 \(1.1\) 告诉我们，结合推广的韦达定理知：\(p_A(t)\) 的零点之和是 \(A\) 的迹 \(tr(A)\)，而零点之积则是 \(A\) 的行列式 \(\mathrm{det} A\)。进一步， 如果 \(p_A(t)\) 的每个零点的重数都是 \(1\)，\(tr(A)\) 是 \(A\) 的特征值之和，而 \(\mathrm{det} A\) 是 \(A\) 的特征值之积 . 其实条件 “ 如果 \(p_A(t)\) 的每个零点的重数都是 \(1\)” 可以不需要，只不过得按照它们作为特征方程的重数来对 \(A\) 的特征值加以计数，下面引入代数重数的概念，

我们约定 \(A \in M_n\) 的特征值总是指这个特征值与其相对应的（代数）重数的合并称谓. 因此无需限制就能说：每个矩阵 \(A \in M_n\) 在复数中恰好有 \(n\) 个特征值，且 \(A\) 的迹和行列式分别是它的特征值之和以及乘积.

我们知道了每一个 \(n\times n\) 复矩阵都有有限多个特征值，故可以给出如下定义.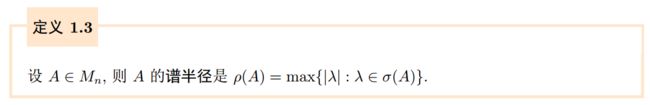

在本小节的最后，再给出一个重要的定理，

  证明：在上一节 特征值和特征向量 的推论 \(1.2\) 知，\(\lambda \in \sigma(A) \Leftrightarrow \lambda + \varepsilon \in \sigma(A+\varepsilon I)\)，我们的目标是 $ \lambda + \varepsilon \neq 0$, 如果 \(A\) 的所有特征值都为零，取 \(\delta=1\)，如果 \(A\) 的某个特征值不为零，则令 \(\delta=\min \{\lvert \lambda \rvert: \lambda \in \sigma(A) , \lambda \neq 0\}\) , 此时任何一个满足 \(0<\lvert \varepsilon \rvert<\delta\) 的 \(\varepsilon\), 必有 \(-\varepsilon \notin \sigma(A)\)，所以 $ \lambda + \varepsilon \neq 0$, 即 \(0 \notin \sigma(A+\varepsilon I)\), 因此 \(A+\varepsilon I\) 是非奇异的.

上述定理表明，一个奇异的复矩阵总可以稍加平移使之成为非奇异的.

 

---

几何重数

开始先给出一个关于特征值的结论，

  证明：由于 \(\mathrm{det}(tI-A^T)=\mathrm{det}(tI-A)^T=\mathrm{det}(tI-A)\), 我们有 \(p_{A^T}(t)=p_A(t)\), 所以有 \(p_{A^T}(\lambda)=0\) 当且仅当 \(p_A(\lambda)=0\). 类似地，\(\mathrm{det}(\bar{t}I-A^*)=\mathrm{det}[(tI-A)^*]=\overline{\mathrm{det}(tI-A)}\), 所以 \(p_{A^*}(\bar{t})=\overline{p_A(t)}\), 又 \(p_{A^*} (\bar{\lambda})=0\) 当且仅当 \(p_A(\lambda)=0\).
 
如果 \(x,y\in \mathbb{C}^n\) 两者都是 \(A\in M_n\) 的与特征值 \(\lambda\) 相伴的特征向量，那么 \(x\) 与 \(y\) 的任何非零的线性组合也是它的与 \(\lambda\) 相伴的特征向量 。实际上，与一个给定的 \(\lambda \in \sigma(A)\) 相伴的所有特征向量组成的集合与零向量合起来作成 \(\mathbb{C}^n\) 的一个子空间，该子空间就是 \(A-\lambda I\) 的零空间，就是齐次线性方程组 \((A-\lambda I)x=0\) 的解集，由秩的关系知其维数是 \(n-\mathrm{rank} (A-\lambda I)\). 该空间有个名字就是特征空间，下面给出特征空间的完整定义，

由 \(Ax=\lambda x\) 便知，\(A\) 的与特征值 \(\lambda\) 相伴的特征空间是一个 \(A\)-不变子空间，需要注意的是，一个 \(A\)-不变子空间不一定就是 \(A\) 的特征空间。特征向量不能为零，所以最小的 \(A\)-不变子空间（不包含有严格的更低维度的非零的 \(A\)-不变子空间） \(W\) 是 \(A\) 的单独一个特征向量所生成的子空间，也就是说 \(\mathrm{dim} W=1\)。介绍完特征空间，就可以定义几何重数了，

可以证明特征值的几何重数小于或者等于它的代数重数的。下面给一个说明：设 \(\alpha\) 是特征多项式 \(p(t)\) 的一个代数重数为 \(k \geqslant 1\) 的零点，当且仅当可以将 \(p(t)\) 写成形式
\[
p(t)=(t-\alpha)^k q(t)
\]
其中 \(q(t)\) 是一个满足 \(q(\alpha) \neq 0\) 的多项式。对 p(t) 求导得：\(p'(t)=k(t-\alpha)^{k-1}q(t)+(t-\alpha)^kq'(t)\), 它表明 \(p'(\alpha)=0\) 当且仅当 \(k>1\). 如果 \(k \geqslant 2\), 那么 \(p''(t)=k(k-1)(t-\alpha)^{k-2}\cdot q(t)+\) 若干个多项式项，其中每一项都含有一个因子 \((t-\alpha)^m, m\geqslant k-1\), 所以 \(p''(\alpha)=0\) 当且仅当 \(k>2\). 重复这一计算表明，\(\alpha\) 是 \(p(t)\) 的 \(k\) 重零点，当且仅当 \(p(\alpha)=p'(\alpha)=\cdots=p^{k-1}(\alpha)=0\) 以及 \(p^k(\alpha) \neq 0\). 据此可以证明一个定理，

  证明：如果 令 \(B=A-\lambda I\), 那么 \(0\) 就是 \(B\) 的一个重数为 \(k\) 的特征值，从而有 \(p_B^{(k)}(0) \neq 0\). 但是 \(p_B^{(k)}(0) =k! (-1)^{n-k}E_{n-k}(B)\), 其中 \(E_{n-k}(B)\) 表示 \(B\) 的 \(n-k\) 阶主子式之和，故有 \(E_{n-k}(B) \neq 0\). 特别地，\(B=A-\lambda I\) 的某个 \(n-k\) 阶主子式不为零，所以 $\mathrm{rank} (A-\lambda I) \geqslant n-k $. 如果 \(k=1\), \(A-\lambda I\) 是奇异的，故而 \(n>\mathrm{rank}(A-\lambda I) \geqslant n-1\), 这就意味着：如果特征值 \(\lambda\) 的代数重数为 \(1\), 那么 \(\mathrm{rank} (A-\lambda I) = n-1\).
 
上述定理即可证明特征值的几何重数小于或者等于它的代数重数，同时还说明了代数重数为 \(1\)，几何重数必定为 \(1\). 需要注意的是并不是说代数重数为 \(1\) 时，代数重数才等于它的几何重数，比如单位矩阵 \(I_2\), \(\lambda=1\)代数重数和几何重数都为 \(2\), 因此它也是半单的。

一个矩阵可对角化，当且仅当它是无亏的；它有完全不同的特征值，当且仅当它是无损的且是无亏的。考虑以下矩阵的特征值 \(\lambda=1\), 矩阵 \(\begin{bmatrix} 1&0 \\ 0 &2 \end{bmatrix}\)，代数重数等于它的几何重数且都是 \(1\), 它是无亏的，单位矩阵 \(I_2\) 是无亏的且是有损的，矩阵 \(\begin{bmatrix} 1&1 \\ 0 &1 \end{bmatrix}\), 几何重数是 \(1\), 代数重数是 \(2\)，它是有亏的且是无损的。
尽管 \(A\) 与 \(A^T\) 有相同的特征值，它们与给定特征值相伴的特征空间有可能是不同的。比如，矩阵 \(A=\begin{bmatrix} 2&3 \\ 0 &4 \end{bmatrix}\), 那么 \(A\) 的与特征值 \(2\) 相伴的（一维）特征空间是由 \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) 生成的，而 \(A^T\) 的与特征值 \(2\) 相伴的特征空间是由 \(\begin{bmatrix} 1& \\ & -3/2 \end{bmatrix}\) 生成的。
 

 

---

读完应该知道点什么

• 每个矩阵 \(A \in M_n\) 在复数中恰好有 \(n\) 个特征值，且 \(A\) 的迹和行列式分别是它的特征值之和以及乘积
• 一个奇异的复矩阵总可以稍加平移使之成为非奇异的
• 特征值的几何重数小于或者等于它的代数重数

转载于:https://www.cnblogs.com/zhoukui/p/7685318.html