【算法】利用有限自动机进行字符串匹配

Timus 1102. Strange Dialog 要求判断给定的输入是否为合法的对话。

---

1102. Strange Dialog

Time Limit: 1.0 second
Memory Limit: 16 MB

One entity named "one" tells with his friend "puton" and their conversation is interesting. "One" can say words "out" and "output", besides he calls his friend by name. "Puton" can say words "in", "input" and "one". They understand each other perfect and even write dialogue in strings without spaces.

You have N strings. Find which of them are dialogues.

Input

In the first line of input there is one non-negative integer N ≤ 1000. Next N lines contain non-empty strings. Each string consists of small Latin letters. Total length of all strings is no more then 10⁷ characters.

Output

Output consists of N lines. Line contains word "YES", if string is some dialogue of "one" and "puton", otherwise "NO".

Sample

input	output
6 puton inonputin oneputonininputoutoutput oneininputwooutoutput outpu utput	YES NO YES NO NO NO

Problem Author: Katya Ovechkina
Problem Source: Tetrahedron Team Contest May 2001

---

题意

one 和 puton 这两个人进行交谈。one 只能够说：out、output 和 puton 这三个单词。而 puton 只能说 in、input 和 one 这三个单词。她们之间的对话是由单词直接连接而成(单词之间没有空格)。

你的任务是判断给定的输入(该输入仅包含小写拉丁字母)是否为合法的对话。

数学背景

一个有限自动机(deterministic finite automaton, DFA) M 是一个 5-元组(Q, q₀, A, Σ, δ)，其中：

• Q 是状态的有限集合
• q₀ ∈ Q 是初始状态
• A Q 是一个接受状态集合
• Σ 是有限的输入字母表
• δ 是一个从 Q × Σ 到 Q 的函数，称为 M 的转移函数

有限自动机开始于状态 q₀，每次读入输入字符串的一个字符。如果有限自动机在状态 q 时读入了输入字符 a，则它从状态 q 变为状态 δ(q, a)(进行了一次转移)。每当其当前状态 q 属于 A 时，就说自动机 M 接受了迄今为止所读入的字符串。没有被接受的输入称为被拒绝的输入。

很多字符串匹配算法都要建立一个有限自动机，它通过对文本字符串 T 进行扫描的方法，找出模式 P 的所有出现位置。用于字符串匹配的自动机都是非常有效的：它们只对每个文本字符检查一次，并且检查每个文本字符的时间为常数。因此，在建立好自动机后所需要的时间为 Θ(n)。

解题思路

我们的任务是判断输入是否只由题目中所给出的六个单词组成。这是一个多模式字符串匹配问题，共有六个模式。

现在，首先需要根据所给的模式构造出相应的字符串匹配自动机，如下所示：

• 状态集合 Q = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 99 }
• 初始状态 q₀ = 0
• 接受状态集合 A = { 0, 1, 2, 3 }
• 输入字母表 Σ = { a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z }
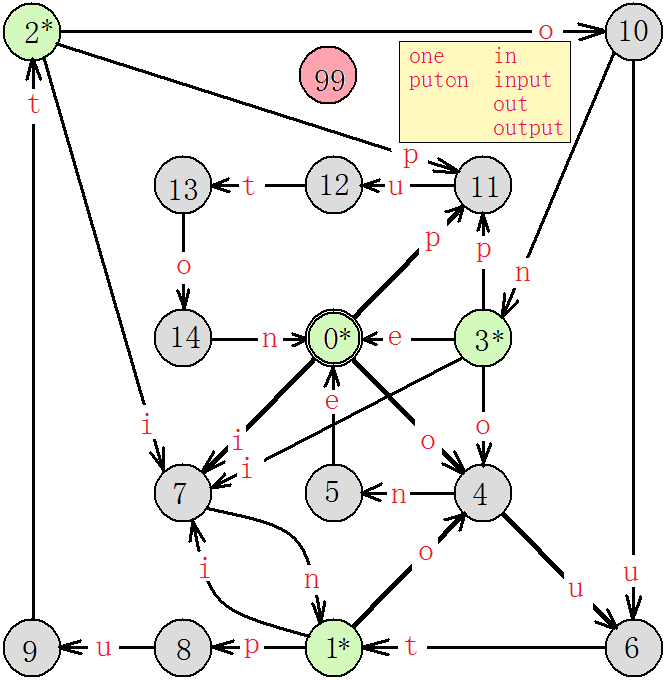
• 转移函数 δ 用状态转换图表示如下：    

这个字符串匹配自动机有以下几个特点：

• 她是一个多模式的字符串匹配自动机
• 她有一个特殊的状态 99，每当该自动机在状态 q 读入了输入字符 a 时，如果在上面的状态转换图中找不到相应的有向边，就转移到这个特殊状态。并且，立即停止该自动机，返回匹配失败。
• 她有多个接受状态，从初始状态 0 开始连续编号。这是为了在程序中方便判断是否匹配。

这个状态转换图中的构造由以下六个模式开始：

one	0 –> 4 –> 5 –> 0*
puton	0 –> 11 –> 12 –> 13 –> 14 –> 0*
in	0 –> 7 -> 1*
out	0 –> 4 –> 6 –> 1*
input	0 –> 7 –> 1* –> 8 –> 9 -> 2*
output	0 –> 4 –> 6 –> 1* –> 8 –> 9 -> 2*

然后，就需要仔细考虑各种状态之间的转移关系了。

最后，相应的 C# 程序如下所示：

using System;

namespace Skyiv.Ben.Timus
{
  // http://acm.timus.ru/problem.aspx?space=1&num=1102
  sealed class T1102
  {
    static readonly int[] a = { 0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 0, 0, 3, 4, 5, 0, 0, 0, 6, 7, 0, 0, 0, 0, 0 };
    static readonly int[,] delta =
    {
      // *   e   i   n   o   p   t   u        有限自动机的转移函数
      { 99, 99,  7, 99,  4, 11, 99, 99 }, //  0 接受状态，初始状态
      { 99, 99,  7, 99,  4,  8, 99, 99 }, //  1 接受状态
      { 99, 99,  7, 99, 10, 11, 99, 99 }, //  2 接受状态
      { 99,  0,  7, 99,  4, 11, 99, 99 }, //  3 接受状态
      { 99, 99, 99,  5, 99, 99, 99,  6 }, //  4 状态
      { 99,  0, 99, 99, 99, 99, 99, 99 }, //  5 状态
      { 99, 99, 99, 99, 99, 99,  1, 99 }, //  6 状态
      { 99, 99, 99,  1, 99, 99, 99, 99 }, //  7 状态
      { 99, 99, 99, 99, 99, 99, 99,  9 }, //  8 状态
      { 99, 99, 99, 99, 99, 99,  2, 99 }, //  9 状态
      { 99, 99, 99,  3, 99, 99, 99,  6 }, // 10 状态
      { 99, 99, 99, 99, 99, 99, 99, 12 }, // 11 状态
      { 99, 99, 99, 99, 99, 99, 13, 99 }, // 12 状态
      { 99, 99, 99, 99, 14, 99, 99, 99 }, // 13 状态
      { 99, 99, 99,  0, 99, 99, 99, 99 }, // 14 状态
    };

    static void Main()
    {
      for (int c, q = 0, n = int.Parse(Console.ReadLine()); n > 0; n--, q = 0)
      {
        while ((c = Console.Read()) != '\n') if (q < 99 && c != '\r') q = delta[q, a[c - 'a']];
        Console.WriteLine((q < 4) ? "YES" : "NO");
      }
    }
  }
}

由于模式中只包括 e、i、n、o、p、t 和 u 这七个字母，数组 a (该数组包括二十六个元素，依次对应二十六个小写拉丁字母)将输入字母表映射为从 0 到 7 的整数，1 到 7 依次对应前面的七个字母，0 对应其它字母。然后，二维数组 delta 表示转移函数 δ，直接由上面的状态转换图得到。剩下的事情就很简单了，Main 方法在 for 循环中依次读入各输入行，然后在 while 循环中执行这个自动机，之后根据自动机的状态输出是否匹配。

进一步的讨论

这道题目的输入规模不超过 10⁷ 个字符，时间限制是 1.0 秒，内存限制是 16 MB。我提交的几个程序的运行时间和内存使用如下表所示：

ID	Date	Author	Problem	Language	Judgement result	Execution time	Memory used
2612947	19:52:41 20 May 2009	skyivben	1102	C++	Accepted	0.062	121 KB
2612930	19:44:58 20 May 2009	skyivben	1102	C#	Accepted	0.125	10 561 KB
2612807	17:17:31 20 May 2009	skyivben	1102	C#	Accepted	0.718	857 KB

上表中第三行就是前面的 C# 程序提交的结果。可以看出，这个 C# 程序的运行时间达到了 0.718 秒，已经接近题目的时间限制了。

如果这个题目的时间限制改为 0.2 秒，那么我们怎么办呢？寻找更高效的字符串匹配算法？

实际上前面的 C# 程序中使用的字符串匹配算法已经非常高效了，几乎没有什么改进的余地了。这个 C# 程序的瓶颈不在于字符串匹配算法，而在于 I/O，即 Console.Read 方法不够高效，而该方法需要在内层循环中被调用大约 10⁷ 次。只要将 Main 方法用以下程序片段代替：

static void Main()
{
  var s = new byte[10000000 + 100];
  int i = 0, n = Console.OpenStandardInput().Read(s, 0, s.Length);
  while (s[i++] != '\n') ;
  for (int c, q = 0; i < n; q = 0)
  {
    while ((c = s[i++]) != '\n') if (q < 99 && c != '\r') q = delta[q, a[c - 'a']];
    Console.WriteLine((q < 4) ? "YES" : "NO");
  }
}

就可以将运行时间缩短到 0.125 秒，如上表中第二行所示。在这个 C# 程序中，我们调用一次 Stream 类的 Read 方法将所有的输入读到的字节数组 s 中，避免了多次调用 Console.Read 方法。因为输入仅包含小写拉丁字母，并不包含汉字等需要两个字节编码的字符，所以可以使用字节数组 byte[]，而不需要使用字符数组 char[]。但是，内存使用就从原来的 857 KB 上升到 10,561 KB 了。

如果时间限制为 0.2 秒，内存限制为 1 MB，那么又要怎么办呢？

只需要将第一个 C# 程序简单地翻译为 C 或者 C++ 程序就行了，用 C/C++ 的 getchar 代替 C# 的 Console.Read 方法。运行时间缩短到 0.062 秒，内存使用降低到 121 KB，如上表中的第一行所示。可见，C/C++ 的 getchar 是非常高效的。实际上，在绝大多数的 C/C++ 实现中，getchar 应该是一个宏，而不是一个函数。

有关这道题目的更多信息，请参见 CSDN 论坛上的一篇贴子：超级郁闷，4个方法都“Memory limit exceeded”。

提到字符串匹配，大多数人都会想起经典的 Knuth-Morris-Pratt 算法。这个由 Donald Knuth (经典名著 The Art of Computer Programming 的作者，著名的电子排版系统 TeX 的研制者)等三人设计的算法是使用有限自动机的单模式匹配算法。它不用计算转移函数 δ，匹配时间为 Θ(n)，只用到辅助数组 π[1, m]，它是在 Θ(m) 的时间内，根据模式预先计算出来的。数组 π 使得我们可以按需要，“现场”有效地计算(在平摊意义上来说)转移函数 δ。

思考题

上面的第二个 C# 程序中有一个 bug，但是这个 bug 在绝大多数情况下都不会表现出来。所以这个程序能够 Accepted。

亲爱的读者，你能够找出这个 bug 吗？

提示，这个 bug 和字符串匹配算法无关，并且第一个 C# 程序中不存在这个 bug 。

---

算法和数据结构目录 Timus 目录