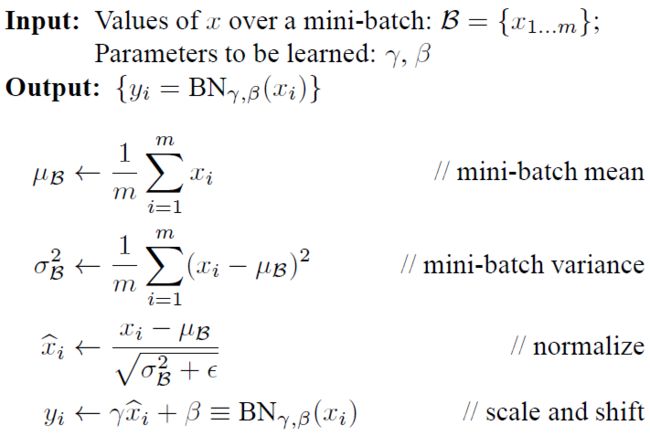Dropout
def dropout_forward(x, dropout_param):
p, mode = dropout_param['p'], dropout_param['mode']
if 'seed' in dropout_param:
np.random.seed(dropout_param['seed'])
mask = None
out = None
if mode == 'train':
#训练环节开启
mask = (np.random.rand(*x.shape) < p) / p
out = x * mask
elif mode == 'test': #测试环节关闭
out = x
cache = (dropout_param, mask)
out = out.astype(x.dtype, copy=False)
return out, cache
def dropout_backward(dout, cache):
dropout_param, mask = cache
mode = dropout_param['mode']
dx = None
if mode == 'train':
dx = dout * mask
elif mode == 'test':
dx = dout
return dx
Batch Normalization
Batch Normalization就是在每一层的wx+b和f(wx+b)之间加一个归一化(将wx+b归一化成:均值为0,方差为1
通常:Means should be close to zero and stds close to one
gamma, beta = np.ones(C), np.zeros(C)
先给出Batch Normalization的算法和反向求导公式:
import numpy as np
def batchnorm_forward(x, gamma, beta, bn_param):
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
sample_mean = np.mean(x, axis=0, keepdims=True) # [1,D]
sample_var = np.var(x, axis=0, keepdims=True) # [1,D]
x_normalized = (x - sample_mean) / np.sqrt(sample_var + eps) # [N,D]
out = gamma * x_normalized + beta
cache = (x_normalized, gamma, beta, sample_mean, sample_var, x, eps)
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
elif mode == 'test':
x_normalized = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma * x_normalized + beta
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache
def batchnorm_backward(dout, cache):
dx, dgamma, dbeta = None, None, None
x_normalized, gamma, beta, sample_mean, sample_var, x, eps = cache
N, D = x.shape
dx_normalized = dout * gamma # [N,D]
x_mu = x - sample_mean # [N,D]
sample_std_inv = 1.0 / np.sqrt(sample_var + eps) # [1,D]
dsample_var = -0.5 * np.sum(dx_normalized * x_mu, axis=0, keepdims=True) * sample_std_inv**3
dsample_mean = -1.0 * np.sum(dx_normalized * sample_std_inv, axis=0, keepdims=True) - \
2.0 * dsample_var * np.mean(x_mu, axis=0, keepdims=True)
dx1 = dx_normalized * sample_std_inv
dx2 = 2.0/N * dsample_var * x_mu
dx = dx1 + dx2 + 1.0/N * dsample_mean
dgamma = np.sum(dout * x_normalized, axis=0, keepdims=True)
dbeta = np.sum(dout, axis=0, keepdims=True)
return dx, dgamma, dbeta
批量归一化(spatia Batch Normalization)
我们已经看到,批量归一化是训练深度完全连接网络的非常有用的技术。批量归一化也可以用于卷积网络,但我们需要调整它一点;该修改将被称为“空间批量归一化”。
通常,批量归一化接受形状(N,D)的输入并产生形状(N,D)的输出,其中我们在小批量维度N上归一化。对于来自卷积层的数据,批归一化需要接受形状(N,C,H,W),并且产生形状(N,C,H,W)的输出,其中N维给出小容器大小,(H,W)维给出特征图的空间大小。
如果使用卷积产生特征图,则我们期望每个特征通道的统计在相同图像内的不同图像和不同位置之间相对一致。因此,空间批量归一化通过计算小批量维度N和空间维度H和W上的统计量来计算C个特征通道中的每一个的平均值和方差。
同样的:#Means should be close to zero and stds close to one
gamma, beta = np.ones(C), np.zeros(C)
代码如下,
def spatial_batchnorm_forward(x, gamma, beta, bn_param):
N, C, H, W = x.shape
x_new = x.transpose(0, 2, 3, 1).reshape(N*H*W, C)
out, cache = batchnorm_forward(x_new, gamma, beta, bn_param)
out = out.reshape(N, H, W, C).transpose(0, 3, 1, 2)
return out, cache
def spatial_batchnorm_backward(dout, cache):
N, C, H, W = dout.shape
dout_new = dout.transpose(0, 2, 3, 1).reshape(N*H*W, C)
dx, dgamma, dbeta = batchnorm_backward(dout_new, cache)
dx = dx.reshape(N, H, W, C).transpose(0, 3, 1, 2)
return dx, dgamma, dbeta