72.编辑距离
题目
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例 1:
输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入: word1 = “intention”, word2 = “execution”
输出: 5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/edit-distance
代码及分析
方法一:递归法
两个单词要进行转换,则要一一遍历两个单词对应的位置,我们首先建立两个指针i, j分别用于指向word1和word2。这里给出了三种操作,修改、增加以及修改,当我们遍历到某个位置时,我们无法判断当前究竟哪种操作最优,因为这一步的操作还会影响到后续的字符。所以针对某个位置的字符,我们需要把这三种操作都执行一次,取其中的最小值。
当word1[i] 和word2[j] 相同时,不需要对word1进行处理,继续遍历即可;
当word1[i] 和word2[j] 不相同时,需要比较三种操作:
\quad (1)修改即是将word1对应位置改为word2中的字符,那么 i 和 j 位置的字符相同,继续遍历下一个字符即可;
\quad (2)增加即是将word1对应位置不变,添加了一个与word2[i]相同的字符,那么接下来需要比较的是word1[i] 和 word2[j+1] ;
\quad (3)删除即是将word1对应位置删除,用word1[j+1]处的字符与word2[i]作比较。
以题中所给案例为例:
word1 = “horse”
word2 = “ros”
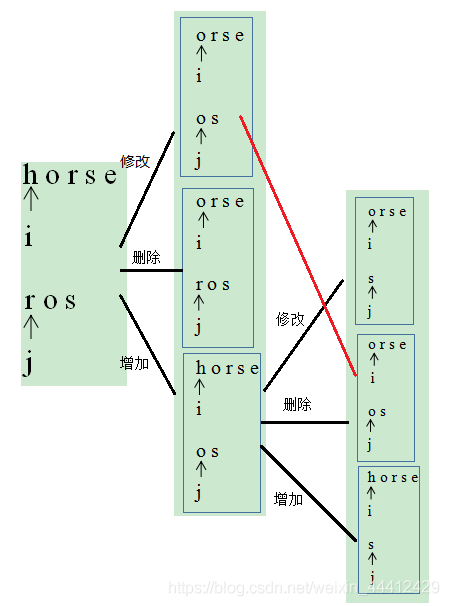
上述图片进行了两步,可以看到红线连接的两处实际上后续的处理是一样的,这样的话会产生大量的重复操作,为了避免这种情况,我们可以建立一个记忆数组memory,其中memory[i][j]
表示当位于word1的 i 位置,word2的 j 位置需要操作的步数。
int minDistance(string word1, string word2) {
int l1 = word1.size();
int l2 = word2.size();
if(word1.empty() && word2.empty())
return 0;
if(l1 == 0)
return l2;
if(l2 == 0)
return l1;
vector<vector<int>> memory(l1, vector<int>(l2,0));
return fun(word1,word2,0,0,memory);
}
int fun(string &word1, string &word2, int i, int j,vector<vector<int>> &memory)
{
if(i == word1.size() && j == word2.size())
return 0;
if(i == word1.size())
return (int)(word2.size()-j);
if(j == word2.size())
return (int)(word1.size()-i);
if(memory[i][j] > 0)
return memory[i][j];
int res = 0;
if(word1[i] == word2[j])
res = fun(word1,word2,i+1,j+1,memory);
else
res = 1+min(fun(word1,word2,i+1,j+1,memory),min(fun(word1,word2,i+1,j,memory),fun(word1,word2,i,j+1,memory)));
return memory[i][j] = res;
}
需要注意的是当fun函数中形参word1,word2不是引用格式时,要比引用格式string &word1, string &word2耗时多几倍。
方法二:动态规划法
这道题我们也可以用动态规划法进行求解,dp[i][j]表示word1 的前i个字符转换成 word2 的前j个字符所需要的步骤(注意还有单词为空的情况)。
当 word1,word2 均为空时,显然有dp[0][0] = 0;
当 word1 为空时,想要将其转换为 word2,只能依次向 word1 中增加对应的字符,故一定有dp[0][i] = i;
当 word2 为空时,想要将 word1 转换为 word2,只能依次删除 word1 中的字符,故一定有 dp[i][0] = i;
而对于dp[i][j],依旧需要根据当前对应字符是否相同分情况讨论:
当 word1[i] 和word2[j] 相同时,不需要对word1进行处理,故此时的最少操作数与i-1,j-1时相同,故有dp[i][j] = dp[i-1][j-1];
当word1[i] 和word2[j] 不相同时,需要比较三种操作选取最小值:
dp[i][j] = 1 + min (dp[i-1][j-1], min(dp[i-1][j],dp[i][j-1]))
其中dp[i-1][j-1], dp[i-1][j], dp[i][j-1] 分别对应着修改、删除以及增加。
举例说明:
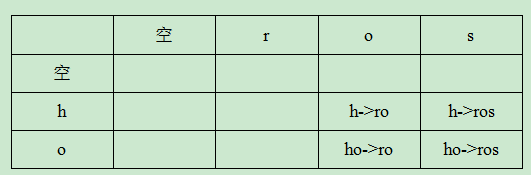
上述表格中,当我们进行求解ho->ros所需的最少操作数时,即dp[2][3],可以有三种操作:
(1)dp[1][2] 为 h->ro ,那么ho->ros 可以通过将o修改为s得到,故其对应修改操作;
(2)dp[1][3] 为 h->ros,那么ho->ros 可以通过将o删除,转化为h->ros,故对应删除操作;
(3)dp[2][2] 为 ho->ro,那么ho->ros 可以通过给ho增加一个s,故对应增加操作。
int minDistance(string word1, string word2) {
int l1 = word1.size();
int l2 = word2.size();
if(word1.empty() && word2.empty())
return 0;
if(l1 == 0)
return l2;
if(l2 == 0)
return l1;
vector<vector<int>> dp(l1+1, vector<int>(l2+1,0));
for(int i = 0; i <= l1; i++) dp[i][0] = i;
for(int i = 0; i <= l2; i++) dp[0][i] = i;
for(int i = 1; i <= l1; i++)
{
for(int j = 1; j <=l2; j++)
{
if(word1[i-1] == word2[j-1])
dp[i][j] = dp[i-1][j-1];
else
dp[i][j] = 1 + min(dp[i-1][j-1], min(dp[i-1][j],dp[i][j-1]));
}
}
return dp[l1][l2];
}
复杂度:
时间复杂度: O(l1* l2) ;
空间复杂度: O(l1* l2) 。