CNN知识点整理

其中1*1卷积核的作用摘抄自https://blog.csdn.net/briblue/article/details/83151475

以下整理刚刚学习的CNN的一些知识点：

一、Input layer:

一般输入数据都会进行一些预处理，常见的有以下步骤（图像处理中）：

1）去均值：把输入数据各个维度都中心化到0

2）归一化：幅度归一化到同样的范围

3）PCA/whitening:用PCA降维，去除特征之间的相关性；白化是对数据每个特征轴上的幅度归一化。

以下两幅图分别帮助理解这三个操作含义。

二、convolutional layer

图像本身具有局部特性。

为什么卷积核有效？

通过图2可以看出，通过第一个卷积核计算后的feature map是一个三维数据，在第三列的绝对值最大，说明原始图片上对应的地方有一条垂直方向的特征；而通过第二个卷积核计算后，第三列的数值为0，第二行的数值绝对值最大，说明原始图片上对应的地方有一条水平方向的特征。可以看出，我们设计的两个卷积核分别能够提取/检测出原始图片的特定的特征。此时我们可以把卷积核理解为特征提取起。每个卷积核可以看作一个特征提取起，不同的卷积核负责提取不同的特征。所以，我们只要把图片数据灌进去，设计好卷积核的尺寸、数量和滑动的步长就可以自动提取出图片的某些特征，从而达到分类效果。

三、activation layer

1) sigmoid

sigmoid函数的缺点：i: 当输入稍微远离了坐标原点，函数的梯度就变得很小了，几乎为零。在神经网络反向传播过程中，我们都是通过微分的链式法则来计算各个权重w的微分的。当反向传播经过了sigmoid函数，这个链条上的微分就很小很小了，况且还可能经过很多个sigmoid函数，最后导致权重w对损失函数几乎没有影响，这样不利用权重的优化，这个问题叫梯度饱和，也叫梯度弥散。

ii: 函数输出不是以0为中心的，这样会使权重更新效率降低。

iii: sigmoid函数要进行指数运算，这个对于计算机来说是比较慢的。

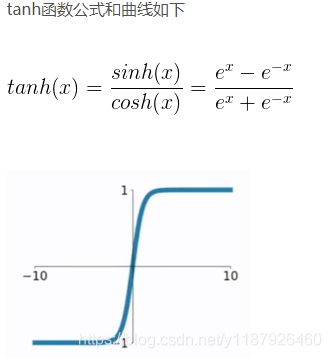
2）Tanh函数

和sigmoid相似的缺点：在输入很大或很小的时候，输出都几乎平滑，梯度很小，不利于权值更新。

相比sigmoid的优点：输出在（-1，1）。中心点在坐标原点，相对对称，叠加后依旧相对对称。

3）ReLu函数

相比于sigmoid和tanh函数的优点：

i: 在输入正数的时候，不存在梯度饱和问题。

ii: 收敛快，求梯度简单，计算速度快。

relu函数的缺点：当输入是负数的时候，relu是完全不被激活的，这就表明一旦输入了负数，relu就会死掉。这个在前向传播过程中，还不算什么问题，有的区域是敏感的，有的是不敏感的。但是到了反向传播过程中，输入负数，梯度就会完全到0，产生梯度饱和（梯度弥散）的问题。

而且relu也不是以0为中心的函数。

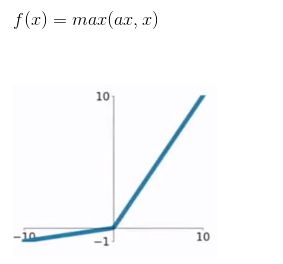
4）Leaky Relu

不会饱和/挂掉，计算也很快。

5）指数线性单元ELU

相比于relu，在输入负数的时候，是有一定的输出的，而且这部分输出还有一定的抗干扰能力。这样可以消除relu死掉的问题，不过还是会有梯度饱和和指数运算的问题。

四、pooling layer

压缩数据和参数的量，减小过拟合。

五、CNN之优缺点：

优点：共享卷积核，对高维数据处理无压力；

无需手动选取特征，训练好权重，即得特征；

分类效果好。

缺点：需要调参，需要大量样本，训练最好用GPU；

物理含义不明确。

六、CNN之fine-tuning

何谓fine-tuning： 使用已用于其他目标，预训练好模型的权重或者部分权重，作为初始值开始训练。。

原因：自己从头训练CNN容易出现问题。

fine-tuning能很快收敛到一个较理想的状态。

做法：复用相同层的权重，新定义层取随机权重初始值。调大新定义层的学习率，调小复用层的学习率。

 七、CNN中1*1卷积核的作用

1) 增加网络的深度。

这涉及到感受野的问题，我们知道卷积核越大，它生成的feature map上单个节点的感受野就越大，随着网络深度的增加，越靠后的feature map上的节点感受野也越大。因此特征也越来越抽象。

但有的时候，我们想在不增加感受野的情况下，让网络加深，为的就是引入更多的非线性。

我们知道，卷积后生成图片的尺寸受卷积核的大小和跨度影响，但如果卷积核是1*1，跨度也是1，那么生成后的图像大小就没有变化。但通常一个卷积过程包括一个激活函数，比如sigmoid和relu。

所以在输入尺寸不发生变化的情况下，却引入了更多的非线性，浙江增强神经网络的表达能力。

2）升维或者降维

卷积后的feature map通道数是与卷积核的个数相同的。

如果输入图片通道是3，卷积核的数量是6，那么生成的feature map通道数就是6，这就是升维；如果卷积核的数量是1，那么生成的feature map只有1个通道，这就是降维。

为什么要用1*1呢？

原因就是数据量的大小，我们知道在训练的时候，卷积核里面的值就是训练的权重，3*3的尺寸是1*1所需内存的9倍，，其它的类似。所以，有时候根据实际情况只想单纯的去提升或者降低feature map的通道，1*1无疑是一个值得考虑的选项。