【论文阅读】NMS系列 结合代码学习 solov2 Matrix NMS

solov2提出了Matrix NMS，这一篇就想把NMS系列总结一下。
Non-Maximum Suppression的翻译是非“极大值”抑制，而不是非“最大值”抑制。这就说明了这个算法的用处：找到局部极大值，并筛除（抑制）邻域内其余的值。

NMS

参考：https://zhuanlan.zhihu.com/p/78504109
在目标检测中，我们需要NMS从堆叠的类别一样的边框中挑出最好的那个。

主要实现的方法就是对于相同类别的，把置信度比自己低，和自己的重叠度即iou大于某一阈值的剔除(把置信度置位0)

算法流程：

• 将所有的框按类别划分，并剔除背景类，因为无需NMS。
• 对每个物体类中的边界框(B_BOX)，按照分类置信度降序排列。
• 在某一类中，选择置信度最高的边界框B_BOX1，将B_BOX1从输入列表中去除，并加入输出列表。
• 逐个计算B_BOX1与其余B_BOX2的交并比IoU，若IoU(B_BOX1,B_BOX2) > 阈值TH，则在输入去除B_BOX2。
• 重复步骤3~4，直到输入列表为空，完成一个物体类的遍历。
• 重复2~5，直到所有物体类的NMS处理完成。
• 输出列表，算法结束

Soft NMS

参考：https://blog.csdn.net/app_12062011/article/details/77963494
motivation：图片上有重叠的两个类别一样的物体，用传统的nms置信度较低的那一个很可能被去除，但其实他们框的是两个不一样的物体。

解决办法：不是一遇到重叠度过高的就去除，而是将阈值降低，降低的方式有liner和高斯。

Matrix NMS

Matrix NMS是在Soft NMS的基础上改进的，因为Soft NMS整个流程是sequential即串行的，不能并行实现（implemented in parallel。

Our Matrix NMS is motivated from Soft- NMS [1].
However, such process is sequential like tradi- tional Greedy NMS and could not be implemented in parallel.

那么作者就想，怎么能实现并行呢？(soft nms求decay factor也就是每次置信度要乘的那个f(iou)是串行的)

decay factor

Matrix NMS就从另一个角度看待问题，他考虑的是一个预测出来的mask $m_j$ 是如何被抑制的。
对于$m_j$它的decay factor受两方面影响：

• 每个预测的$m_i$对$m_j$的penalty ($s_i>s_j$)
  这个penalty通过$f(io{u}_{i,j})$就直接可以得到
• $m_i$被抑制的概率
  这个$m_i$被抑制的概率就不容易算了，但是这个概率和IOU正相关，所以Matrix nms直接用和$m_i$的iou最大（重叠度最高）的预测来近似这个概率（iou最大 那f(iou)最小，所以公式如下，反正就是找和$m_i$重叠度最高的）
  
  通过以上两点，得到$m_j$的decay factor：
  
  我自己理解:
  对于$mask{m}_j$，我们要通过$s_j\ast decayfactor$来得到新的置信度$s_j$。
  那soft nms是依次遍历和$m_j$相同类且置信度比他高的那些$m_i$，然后decay factor 就是 $f(io{u}_{i,j})$。
  Matrix nms 想并行计算，想通过矩阵一次性求decay factor，他就想对$m_j$置信度更新的那些$m_i$，它们自己如果被抑制了，那对我的抑制作用就没了。 你人都没了，你还影响我？然后$m_i$被抑制最有可能就是和他重叠度最大的那个mask干的。

$f(io{u}_{i,j})$ decremented functions

和soft nms一样，有线性的和高斯的

• linear
  
• Gaussian
  

代码解读

官方代码：
solov2的/SOLO/mmdet/core/post_processing/matrix_nms.py 的matrix_nms函数

def matrix_nms(seg_masks, cate_labels, cate_scores, kernel='gaussian', sigma=2.0, sum_masks=None):
    """Matrix NMS for multi-class masks.

    Args:
        seg_masks (Tensor): shape (n, h, w)
        cate_labels (Tensor): shape (n), mask labels in descending order
        cate_scores (Tensor): shape (n), mask scores in descending order
        kernel (str):  'linear' or 'gauss' 
        sigma (float): std in gaussian method
        sum_masks (Tensor): The sum of seg_masks

    Returns:
        Tensor: cate_scores_update, tensors of shape (n)
    """

1. 得到NxN pairwise IoU Matrix
   论文中第一步是得到一个NxN的iou矩阵，也就是这N个mask 每个和其他的mask的iou

We first compute a N ×N pairwise IoU matrix for the top N predictions sorted descending by score. For binary masks, the IoU matrix could be efficiently implemented by matrix opera- tions.

伪代码：

• 首先是伪代码的第一部分：reshape for computation Nx(HW)
  先按置信度选出top N个mask，文章中N选的是500。得到的seg_masks是[N,HxW]，也就是每一行是一个mask的所有像素值

    n_samples = len(cate_labels)#N
    if n_samples == 0:
        return []
    if sum_masks is None:
        sum_masks = seg_masks.sum((1, 2)).float()
    seg_masks = seg_masks.reshape(n_samples, -1).float()#[N,HxW]

• 伪代码的第二部分：pre−compute the IoU matrix: NxN
  这一部分就是计算这个iou 矩阵，iou就是要算交集和并集
  对于$m_i$和$m_j$来说，
  他们的交集就是相同位置都是1的像素点的总和
  并集就是 $m_i$像素值的和+$m_j$像素值的和-交集的值，注意代码中sum_masks_x只是把每个mask的像素值按列扩充成[N,N]了，以备后续和别人加 真正的union是
  union:sum_masks_x + sum_masks_x.transpose(1, 0) - inter_matrix

    # inter.
    inter_matrix = torch.mm(seg_masks, seg_masks.transpose(1, 0))#[N,N] torch.mm是进行矩阵相乘，对每个mask i 和 mask j 的值对应相乘加起来 作为inter_matrix[i][j]的值 即mask i和mask j相交的像素数
    """
    tensor([[4081., 3931., 3918.,  ..., 3645.,    0.,    0.],
        [3931., 3937., 3826.,  ..., 3615.,    0.,    0.],
        [3918., 3826., 4067.,  ..., 3614.,    0.,    0.],
        ...,
        [3645., 3615., 3614.,  ..., 6124.,    0.,   50.],
        [   0.,    0.,    0.,  ...,    0.,  273.,    0.],
        [   0.,    0.,    0.,  ...,   50.,    0.,   50.]], device='cuda:0')
    """
    # union.
    sum_masks_x = sum_masks.expand(n_samples, n_samples)#[N]->[N,N] 每一列的值都相同 union:sum_masks_x + sum_masks_x.transpose(1, 0) - inter_matrix
    # iou.
    iou_matrix = (inter_matrix / (sum_masks_x + sum_masks_x.transpose(1, 0) - inter_matrix)).triu(diagonal=1)#[N,N] triu 得到上三角矩阵 diagonal=1表示不包含对角线
    """
    tensor([[0.0000, 0.9618, 0.9262,  ..., 0.5556, 0.0000, 0.0000],
        [0.0000, 0.0000, 0.9157,  ..., 0.5608, 0.0000, 0.0000],
        [0.0000, 0.0000, 0.0000,  ..., 0.5495, 0.0000, 0.0000],
        ...,
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0082],
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0000],
        [0.0000, 0.0000, 0.0000,  ..., 0.0000, 0.0000, 0.0000]],
       device='cuda:0')
    """

• 得到类别相同 label_specific matrix
  这一部分伪代码没有体现，但上一部我们得到的iou_matrix是和其它所有mask的交集，但我们知道nms其实就是筛掉和自己类别相同的

    # label_specific matrix.
    cate_labels_x = cate_labels.expand(n_samples, n_samples)
    label_matrix = (cate_labels_x == cate_labels_x.transpose(1, 0)).float().triu(diagonal=1)#[N,N] 把mask i 和maski 的label一样的值为1 
    """
    tensor([[0., 1., 1.,  ..., 0., 0., 0.],
        [0., 0., 1.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        ...,
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]], device='cuda:0')
    """

2. max IoU for each: NxN 计算decay factor的分母

Then we get the most overlapping IoUs by column-wise max on the IoU matrix.

这一部分我们求的是mi被抑制的概率，还记得论文是怎么表示这一部分的吗，就是用和他重叠度最高的那个iou来表示

    # IoU compensation 
    compensate_iou, _ = (iou_matrix * label_matrix).max(0)#[N] 对每个mask i 找到和他相同类别的 最大iou 即论文伪代码的ious_cmax max(0)是找到每一列的最大值
    compensate_iou = compensate_iou.expand(n_samples, n_samples).transpose(1, 0)#[N,N] 每一列的值一样

3. 计算decay factor

Next, the decay factors of all higher scoring predictions are computed, and the decay fac- tor for each prediction is selected as the most effect one by column-wise min (Eqn. (4)).

上面已经得到了分子要的decay_iou:和自己类别相同且置信度比自己高的iou的值
分母要的compensate_iou: 重叠度最高的最大iou
那算decay factor就是看用高斯还是线性的，套公式即可

    # IoU decay 
    decay_iou = iou_matrix * label_matrix #[N,N] decay_iou[i][j] mask i 和maskj 的iou，且类别相同

    # matrix nms 
    if kernel == 'gaussian':
        decay_matrix = torch.exp(-1 * sigma * (decay_iou ** 2))
        compensate_matrix = torch.exp(-1 * sigma * (compensate_iou ** 2))
        decay_coefficient, _ = (decay_matrix / compensate_matrix).min(0)
    elif kernel == 'linear':
        decay_matrix = (1-decay_iou)/(1-compensate_iou)
        decay_coefficient, _ = decay_matrix.min(0)#[N] decay_coefficient 对应的就是这N个mask被抑制的概率 就是论文的decay factor
    else:
        raise NotImplementedError

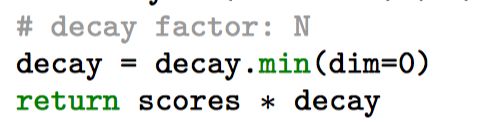
4. 得到新的置信度

Finally, the scores are updated by the decay factor. For usage, we just need threshing and selecting top-k scoring masks as the final predictions.

    # update the score.
    cate_scores_update = cate_scores * decay_coefficient
    return cate_scores_update