密码学(一)
目录
- 模运算
- 离散对数难题
- 迪菲-赫尔曼秘钥交换
- 欧拉函数 与 欧拉定理
- RSA 非对称加密算法
模运算
-
取模(mod)和取余(rem)的区别
取模运算(mod)和取余运算(rem)两个概念有重叠的部分,但又不完全一致。主要区别在于对负整数进行除法运算时操作不同:
取模运算 在计算商值时 商值向 负无穷方向 舍入,即商取小原则
取余运算 在计算商值时 商值向 0方向 舍入,即商靠0原则取模主要是用于计算机术语中,取余则更多是数学概念
-
计算步骤
假设有整数 A 和 B,那么取模(或取余)运算可以分为两步进行:
- 计算整数商:C = A / B
- 计算模/余数:R = A - (C x B)
即计算模:A mod B = A - B(A / B),其中(A / B)表示整数商
-
例子
简述(取模) 求商值(取模、取余的区别在于求商值方式不同) 取模过程 取模值 5 mod 3 = 2 5 / 3 = 1.66 商取小原则 商 = 1 5 - 3 x 1 = 2 2 -5 mod 3 = 1 -5 / 3 = -1.66 商取小原则 商 = -2 -5 - (3 x -2) = 1 1 5 mod -3 = -1 5 / -3 = -1.66 商取小原则 商 = -2 5 - (-3 x -2) = -1 -1 -5 mod -3 = -2 -5 / -3 = 1.66 商取小原则 商 = 1 -5 - (-3 x 1) = -2 -2 简述(取余) 求商值(取模、取余的区别在于求商值方式不同) 取余过程 取余值 5 rem 3 = 2 5 / 3 = 1.66 商靠0原则 商 = 1 5 - 3 x 1 = 2 2 -5 rem 3 = -2 -5 / 3 = -1.66 商靠0原则 商 = -1 -5 - (3 x -1) = - 2 -2 5 rem -3 = 2 5 / -3 = -1.66 商靠0原则 商 = -1 5 - (-3 x -1) = 2 2 -5 rem -3 = -2 -5 / -3 = 1.66 商靠0原则 商 = 1 -5 - (-3 x 1) = - 2 -2 -
模的理解
模是指一个计量系统的计数范围:
如时钟,以12个整点为计算范围,则模为 12
计算机也是一个计量机器,模为 32位 或者 64位32位计算机正常理解 在模 范围内能表达的数 有 [0, 2³²-1]
那么负数该怎么表示呢?
所以出现了补码:也就是 正数 + 负数 正好达到模的溢出阀值 2³²,这也是在计算机中负数是用补码方式表示的原因关于补码的例子:
在以12为模的时钟中,假设当前时针指向10点,而准确时间是6点,调整时间可有以下两种拨法:- 逆时针倒拨 4 小时,即:10 - 4 = 6 ,(10 - 4) mod 12 = 6
- 顺时针顺拨 8 小时,即 10 + 8 = 12 + 6 = 6,(10 + 8) mod 12 = 6
在以12为模的系统中,加8 和 减4 效果是一样的;因此凡是减4运算,都可以用加8运算来代替。对 模 而言,8 和 4 互为补数。
实际上在以12为模的系统中:11和1、10和2、9和3、8和4、7和5、6和6 都具有这个特性,都互为补数。
共同的特点是两者相加等于模。对一个数取模,实质上是获取该数在计量器上产生的溢出的量,该数的值在计量器上表示不出来,计量器上只能表示出该数取模后的结果。
任何有模的计量器,均可化为加减法运算 -
计算机中取模的应用
取模的本质是:取模的值,必定会落在模的范围内;所以,计算机领域引用该特性,使元素路由算法不超出边界,并有规则地存放
元素路由算法分为以下两步:- 确定模(确定范围)
- 元素取模,使元素有规则的落入模的范围内的容器中
如:HashMap、数据库分表、分布式节点路由算法等
-
注意
不同编程语言中,% 的含义不同:Java 中 % 是取余运算;Python 中 % 是取模运算
设 A mod B = C,A 叫做 被模数,B 叫做 模数,C 叫做模值
5 mod 3 = 2 例子中,5 为被模数,3 为模数,2 为模值
离散对数难题
-
相关数学概念
质数是指在大于 1 的自然数中,除了 1 和 它本身 以外不再有其他因数的自然数。
合数指自然数中除了能被 1 和 本身 整除外,还能被其他数(0除外)整除的数。
唯一分解定律(算术基本定理):每个大于 1 的自然数均可写为质数的积,而且这些质因数按大小排列之后,写法有且仅有一种方式。即任意正整数有且只有一种质因数分解。如果将每个正整数描述为一个带有不同编号的锁,每个编号的锁的独特钥匙,就是其质因数分解。就像任何两个锁的钥匙都不同,任何两个数的质因数分解也不同。
比如:
13 = 13
14 = 2 x 7
15 = 3 x 5
16 = 2 x 2 x 2 x 2互质自然数是公因数只有 1 的两个自然数,互质整数是公因数只有 1 的两个整数。互质自然数是互质整数的特殊情形。
质数与除自身外的任意正整数互质。同余:如果两个数 a 和 b 之差能被 m 整除,那么我们就说 a 和 b 对模数 m 同余(a 和 b 关于 m 同余)
对数:一般地, a x = N a^x=N ax=N( a > 0 a > 0 a>0 且 a ≠ 1 a \neq 1 a=1),那么幂指数 x x x 叫做以 a a a 为底 N N N 的对数,记作 log a N \log_a{N} logaN。其中, a a a 叫做对数的底数, N N N 叫做真数。
-
离散对数难题简介
在整数中,离散对数是一种基于同余运算和原根的一种对数运算
在任何群G(初等群论)中,可为所有整数 k 定义一个幂数为 b x b^x bx,而离散对数 log b a \log_b{a} logba 是指使得 b x b^x bx ≡ a 的整数 k
离散对数在一些特殊情况下可以快速计算,然而,通常没有高效的方法来计算离散对数
公钥密码学中几个重要算法的基础,都是假设寻找离散对数的问题的解时,在仔细选择过的群中,并不存在有效率的求解算法举个例子,以下是一个典型的离散对数难题:
已知公式: 3 x m o d 17 3^x ~~mod~~ 17 3x mod 17(这里采用质数做模数,3 为17 的一个原根),当 x ∈ ( 0 , 17 ) x \in (0,17) x∈(0,17)时,可以很容易求得 x 在各个情况下的结果X 运算 结果 x = 1 3 1 m o d 17 3^1 ~~mod~~ 17 31 mod 17 3 x = 2 3 2 m o d 17 3^2 ~~mod~~ 17 32 mod 17 9 x = 3 3 3 m o d 17 3^3 ~~mod~~ 17 33 mod 17 10 x = 4 3 4 m o d 17 3^4 ~~mod~~ 17 34 mod 17 13 x = 5 3 5 m o d 17 3^5 ~~mod~~ 17 35 mod 17 5 x = 6 3 6 m o d 17 3^6 ~~mod~~ 17 36 mod 17 15 x = 7 3 7 m o d 17 3^7 ~~mod~~ 17 37 mod 17 11 x = 8 3 8 m o d 17 3^8 ~~mod~~ 17 38 mod 17 16 x = 9 3 9 m o d 17 3^9 ~~mod~~ 17 39 mod 17 14 x = 10 3 10 m o d 17 3^{10} ~~mod~~ 17 310 mod 17 8 x = 11 3 11 m o d 17 3^{11} ~~mod~~ 17 311 mod 17 7 x = 12 3 12 m o d 17 3^{12} ~~mod~~ 17 312 mod 17 4 x = 13 3 13 m o d 17 3^{13} ~~mod~~ 17 313 mod 17 12 x = 14 3 14 m o d 17 3^{14} ~~mod~~ 17 314 mod 17 2 x = 15 3 15 m o d 17 3^{15} ~~mod~~ 17 315 mod 17 6 x = 16 3 16 m o d 17 3^{16} ~~mod~~ 17 316 mod 17 1 观察上面的表格,已知 3 x m o d 17 3^x ~~mod~~ 17 3x mod 17,当 x ∈ ( 0 , 17 ) x \in (0,17) x∈(0,17) 时,结果会在(0,17)上均匀分布,即结果等可能地出现在 0 和 17 中间的任何整数上
相反地,如果已知: 3 x m o d 17 = 12 3^x ~~mod~~ 17 = 12 3x mod 17=12(这里采用质数做模数,3 为17 的一个原根),要求 x x x 的值,那么我们只能采用试错法,求出匹配的指数
这是一种正算容易,反算困难的数值过程。这有多难呢?如果模数较小,还很容易试出 x x x 的值,但模数若是长达几百位的质数,那么想试出 x x x 的值是不切实际的,即使是借助世界上最强大的计算机,要遍历所有可能情况也需要上千年时间。
离散对数是一种单向函数,单向函数的强度取决于反向过程所需要的时间
-
离散对数难题的作用
离散对数正算容易,反算困难的特点,可以用于信息的加密和解密。
以上面 3 x m o d 17 = 12 , x = 13 3^x ~~mod~~ 17 = 12, x = 13 3x mod 17=12,x=13 为例:
3 3 3 为原信息, 12 12 12 是加密后的信息, 3 x m o d 17 3^x ~~mod~~ 17 3x mod 17 是一个公开的加密过程, x = 13 x = 13 x=13 为秘钥。在不知道秘钥 x = 13 x = 13 x=13 的情况下,即使知道加密过程 3 x m o d 17 3^x ~~mod~~ 17 3x mod 17,并且截获了加密过的信息 12 12 12,也难以通过反算得到原信息 3 3 3但是,这里有个问题:信息发送者使用秘钥 x = 13 x = 13 x=13 对信息进行加密,信息接受者也需要知道秘钥 x = 13 x = 13 x=13,才能对信息进行解密,那么如何安全地传输秘钥呢?请看下面的迪菲-赫尔曼秘钥交换。
迪菲-赫尔曼秘钥交换
-
概述
迪菲-赫尔曼秘钥交换算法是一种建立秘钥的算法,而不是一种加密信息的算法,即迪菲-赫尔曼秘钥交换算法解决的是秘钥安全传输的问题,通讯双方在安全拿到秘钥之后,还需要通过秘钥使用其他加密算法,对通讯的信息进行加密和解密。
迪菲-赫尔曼秘钥交换算法的有效性和安全性依赖于计算离散对数的难度。
-
举例
举一个现实生活中颜料混合的例子。
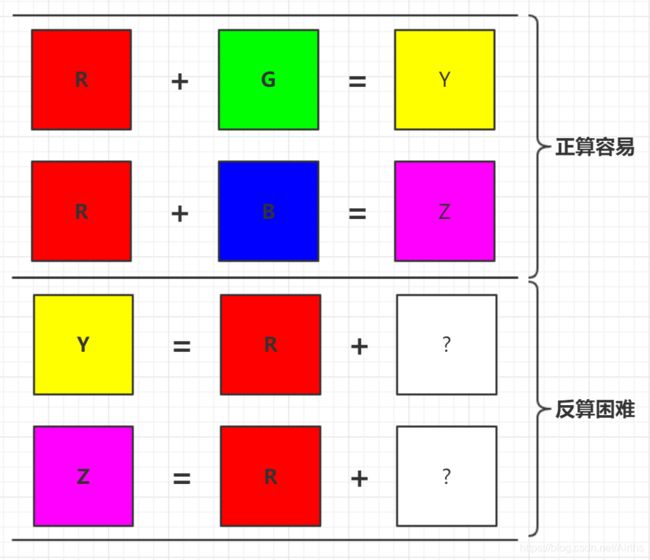
写代码的兄弟们注意了,例子里面说的是现实生活中画画颜料的混合,而不是计算机中 RGB 值的加减(因为在计算机中,知道了两种颜色的 RGB,可以很容易地计算出这两种颜色的差值)。虽然我们很容易:
通过混合 红色颜料R 和 绿色颜料G,得到 黄色颜料Y
通过混合 红色颜料R 和 蓝色颜料B,得到 紫色颜料Z
但是我们很难:
从 黄色颜料Y 中分离出 红色颜料R 和 绿色颜料G
从 紫色颜料Z 中分离出 红色颜料R 和 蓝色颜料B
这个过程就像
我们很容易正算出 3 13 m o d 17 = 12 3^{13} ~~mod~~ 17 = 12 313 mod 17=12
但我们很难反算出 3 x m o d 17 = 12 3^{x} ~~mod~~ 17 = 12 3x mod 17=12
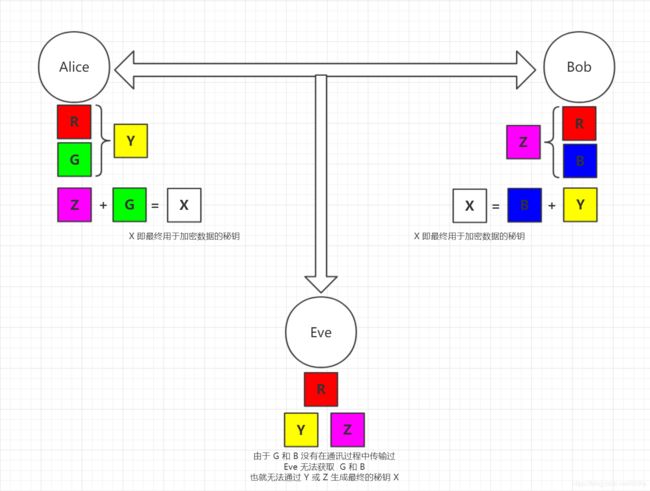
假设有通讯的双方 Alice 和 Bob,他们需要调制一种秘密颜色 并且 不能让窃听者 Eve 知道,于是 Alice 和 Bob 执行了以下步骤:
- Alice 和 Bob 共同公布一种颜料:红色颜料R,窃听者 Eve 获取到红色 颜料R
- Alice 随机生成一种不对外公布的颜料: 绿色颜料G,Bob 和窃听者 Eve 都无法获取到 绿色颜料G
- Alice 混合 红色颜料R 和 绿色颜料G,生成 黄色颜料Y
- Alice 公布 黄色颜料Y,Bob 和窃听者 Eve 都获取到 黄色颜料Y
- Bob 随机生成一种不对外公布的颜料: 蓝色颜料B,Alice 和窃听者 Eve 都无法获取到 蓝色颜料B
- Bob 混合 红色颜料R 和 蓝色颜料B,生成 紫色颜料Z
- Bob 公布 紫色颜料Z,Alice 和窃听者 Eve 都获取到 紫色颜料Z
- Alice 使用获取到的 紫色颜料Z 和 自己不对外公布的 绿色颜料G,生成了用于通讯的秘密颜料:白色颜料X
- Bob 使用获取到的 黄色颜料Y 和 自己不对外公布的 蓝色颜料B 生成了用于通讯的秘密颜料:白色颜料X
- 由于窃听者 Eve 缺少 绿色颜料G 和 蓝色颜料B,窃听者 Eve 就无法通过截取到的 黄色颜料Y 或者 紫色颜料Z 来生成秘密颜料:白色颜料X
整个过程看起来有点复杂,我这里理一理:
Alice 的 白色颜料X = (红色颜料R + 蓝色颜料B) + 绿色颜料G
Bob 的 白色颜料X = (红色颜料R + 绿色颜料G) + 蓝色颜料B
-
迪菲-赫尔曼秘钥交换算法的数学描述
参考上面的公式: 3 x m o d 17 3^x ~~mod~~ 17 3x mod 17, x ∈ ( 0 , 17 ) x \in (0,17) x∈(0,17)
定义如下离散对数:- 模数 p p p 为质数( p p p 相当于 17 17 17)
- a a a 为 p p p 的一个原根( a a a 相当于 3 3 3)
- 为其各次幂产生从 1 1 1 到 p − 1 p - 1 p−1 的所有整数根(相当于 x ∈ [ 1 , 16 ] x \in [1,16] x∈[1,16])
那么数值
a 1 m o d p a^1 ~~mod~~ p a1 mod p 、 a 2 m o d p a^2 ~~mod~~ p a2 mod p 、… … 、 a 16 m o d p a^{16} ~~mod~~ p a16 mod p
是各不相同的整数,并且以某种排列方式组成了从 1 1 1 到 p − 1 p - 1 p−1 的所有整数对于一个整数 b b b 和 质数 p p p 的一个原根 a a a,可以找到惟一的指数 i i i,使得
b = a i m o d p , i ∈ [ 1 , p − 1 ] , b ∈ [ 1 , p − 1 ] , b = a^i ~~mod~~ p~,~~i \in [1,p - 1],~~b \in [1,p - 1], b=ai mod p , i∈[1,p−1], b∈[1,p−1],
称指数 i i i 为 b b b 的以 a a a 为基数的模 p p p 的离散对数基于此背景知识,迪菲-赫尔曼秘密钥交换算法的数学描述如下:
-
定义两个全局公开的参数,一个质数 p p p 和 一个整数 a a a, a a a 是 p p p 的一个原根
-
当 Alice 和 Bob 需要建立一个秘钥时
Alice 选择一个作为私有密钥的随机数 X a X_a Xa,并计算公开秘钥 Y a = a X a m o d p Y_a = a^{X_a}~~mod~~p~~ Ya=aXa mod p 。
Alice 对 X a X_a Xa 的值保密存放并使得 Y a Y_a Ya 能被 Bob 公开获得。
类似地,Bob 选择一个作为私有密钥的随机数 X b X_b Xb,并计算公开秘钥 Y b = a X b m o d p Y_b = a^{X_b}~~mod~~p~~ Yb=aXb mod p 。
Bob 对 X b X_b Xb 的值保密存放并使得 Y b Y_b Yb 能被 Alice 公开获得。 -
Alice 产生共享秘密密钥的计算方式是 K = Y b X a m o d p K={Y_b}^{X_a}~~mod~~ p~~ K=YbXa mod p 。
同样地,Bob 产生共享秘密密钥的计算方式是 K = Y a X b m o d p K={Y_a}^{X_b}~~mod~~ p~~ K=YaXb mod p 。
这两个计算产生相同的结果:K = Y b X a m o d p K={Y_b}^{X_a}~~mod~~p~~~~~~~~~~~~~~~~~~~~~ K=YbXa mod p // 这里是 Alice 秘钥的计算方式
= ( a X b m o d p ) X a m o d p ~~~~~=({a}^{X_b}~~mod~~p)^{X_a}~~mod~~p =(aXb mod p)Xa mod p
= ( a X b ) X a m o d p ~~~~~=({a}^{X_b})^{X_a}~~mod~~p =(aXb)Xa mod p
= a X b X a m o d p ~~~~~={a}^{X_bX_a}~~mod~~p =aXbXa mod p
= ( a X a ) X b m o d p ~~~~~=({a}^{X_a})^{X_b}~~mod~~p =(aXa)Xb mod p
= ( a X a m o d p ) X b m o d p ~~~~~=({a}^{X_a}~~mod~~p)^{X_b}~~mod~~p =(aXa mod p)Xb mod p
= Y a X b m o d p ~~~~~={Y_a}^{X_b}~~mod~~p~~~~~~~~~~~~~~~~~~~~~ =YaXb mod p // 这里是 Bob 秘钥的计算方式
-
因为 X a X_a Xa 和 X b X_b Xb 是保密的,窃听者 Eve 可以利用的参数只有 p p p、 a a a 、 Y a Y_a Ya 、 Y b Y_b~~ Yb 。因而窃取者 Eve 被迫计算离散对数来确定秘钥。例如,要获取 Bob 的秘钥 X b X_b Xb,窃听者 Eve 必须先计算
X b i n d a , p Y b {X_b}~ind~a~,~p^{Y_b} Xb ind a , pYb
然后再采用与 Bob 同样的方法计算公共秘钥 K K~~ K 。
-
迪菲-赫尔曼秘钥交换算法的优缺点
优点:
- 仅当需要时才生成密钥,减小了将密钥存储很长一段时间而致使遭受攻击的机会。
- 除对全局参数的约定外,密钥交换不需要事先存在的基础结构。
缺点:
-
它是计算密集性的,因此容易遭受阻塞性攻击,即对手请求大量的密钥。受攻击者花费了相对多的计算资源来求解无用的幂系数而不是在做真正的工作。
-
容易遭受中间人攻击。窃听者 Eve 在和 Alice 通信时扮演 Bob;在和 Bob 通信时扮演 Alice。Alice 和 Bob 都与窃听者 Eve 协商了一个密钥,然后窃听者 Eve 就可以监听和传递通信信息。中间人的攻击按如下进行:
- Bob 在给 Alice 的报文中发送他的公开密钥 Y b Y_b Yb
- 窃听者 Eve 截获并解析该报文。窃听者 Eve 将 Bob 的公开密钥保存下来并给 Alice 发送报文,该报文具有 Bob 的用户 ID 但使用窃听者 Eve 的公开密钥 Y c Y_c Yc,报文仍按照好像是来自 Bob 的样子被发送出去。Alice 收到窃听者 Eve 的报文后,将 Y c Y_c Yc 和 Bob 的用户 ID 存储在一块。类似地,窃听者 Eve 使用 Y c Y_c Yc 向 Bob 发送好像来自 Alice 的报文。
- Bob 基于 X b X_b Xb 和 Y c Y_c Yc 计算秘密密钥 K 1 K_1 K1。Alice 基于 X a X_a Xa 和 Y c Y_c Yc 计算秘密密钥 K 2 K_2 K2。窃听者 Eve 使用 X c X_c Xc 和 Y b Y_b Yb 计算 K 1 K_1 K1,并使用 X c X_c Xc 和 Y a Y_a Ya 计算 K 2 K_2 K2。
- 从现在开始,窃听者 Eve 就可以转发 Alice 发给 Bob 的报文或转发 Bob 发给 Alice 的报文,在途中根据需要修改它们的密文。使得 Alice 和 Bob 都不知道他们在和窃听者 Eve 共享通信。
-
当互相通讯的用户变多的时候,共享秘钥会变得难以管理。例如,如果 Alice 需要和很多人通讯:Bob,Claire,Duck,Ella,…,那么 Alice 跟 Bob 通讯需要生成 共享秘钥 K 1 K_1 K1,Alice 跟 Claire 通讯需要生成 共享秘钥 K 2 K_2 K2,Alice 跟 Duck 通讯需要生成 共享秘钥 K 3 K_3 K3,…
欧拉函数 与 欧拉定理
-
欧拉函数
对于一个正整数 x x x,小于 x x x 且和 x x x 互质的正整数的个数,记做 φ ( x ) φ(x) φ(x)。其中 φ ( 1 ) φ(1) φ(1)被定义为 1 1 1。
欧拉函数重要性质:
- 若 p p p 是质数,则有 φ ( p ) = p − 1 φ(p)=p-1 φ(p)=p−1
- 若 x x x, y y y 互质,则有 φ ( x y ) = φ ( x ) φ ( y ) φ(xy)=φ(x)φ(y) φ(xy)=φ(x)φ(y)
- 若 x x x, y y y 均为质数,则有 φ ( x y ) = φ ( x ) φ ( y ) = ( x − 1 ) ( y − 1 ) φ(xy)=φ(x)φ(y)=(x-1)(y-1) φ(xy)=φ(x)φ(y)=(x−1)(y−1)
- 若 x x x 是质数 p p p 的 k k k 次幂,即 x = p k x=p^k x=pk,则有 φ ( x ) = p k − p k − 1 φ(x)=p^{k}-p^{k-1} φ(x)=pk−pk−1
补充:
- 欧拉函数是欧拉研究了质数的分布性质后得出的一个重要函数,它衡量的是数的可分性。
- 通常情况下,计算欧拉函数的结果很难,除了一种特殊情况:若 p p p 是质数,则有 φ ( p ) = p − 1 φ(p)=p-1 φ(p)=p−1
-
欧拉定理
若 m m m, n n n 为正整数,且 m m m, n n n 互质,则有:
m φ ( n ) ≡ 1 m o d n m^{φ(n)}\equiv1~~mod~~n~~~~ mφ(n)≡1 mod n 或者 m φ ( n ) m o d n ≡ 1 ~~~~m^{φ(n)}~~mod~~n\equiv1 mφ(n) mod n≡1欧拉定理的重要性质:
- 利用欧拉定理降幂: m b m o d n = m b m o d φ ( n ) m o d n m^{b}~~mod~~n=m^{b~~mod~~φ(n)}~~mod~~n mb mod n=mb mod φ(n) mod n
- 如果 b ≥ φ ( n ) b\geqφ(n) b≥φ(n),则有 m b m o d n = m b m o d φ ( n ) + φ ( n ) m o d n m^{b}~~mod~~n=m^{b~~mod~~φ(n)+φ(n)}~~mod~~n mb mod n=mb mod φ(n)+φ(n) mod n
-
模反元素
如果两个正整数 e e e 和 φ ( n ) φ(n) φ(n) 互质,那么一定可以找到整数 d d d,使得 e d − 1 ed - 1 ed−1 被 φ ( n ) φ(n) φ(n) 整除,或者说 e d ed ed 被 φ ( n ) φ(n) φ(n) 除的余数是 1 1 1。这时, d d d 就叫做 e e e 关于 φ ( n ) φ(n) φ(n) 的 模反元素:
e d m o d φ ( n ) ≡ 1 ed~~ mod~~φ(n)~~\equiv1~~~ ed mod φ(n) ≡1 或者 e d − 1 m o d φ ( n ) ≡ 0 ~~~ed - 1~~ mod~~φ(n)~~\equiv0 ed−1 mod φ(n) ≡0欧拉定理可以用来证明模反元素必然存在
RSA 非对称加密算法
-
RSA 非对称加密算法简介
RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用。RSA 是1977 年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。当时他们三人都在麻省理工学院工作。RSA 就是他们三人姓氏开头字母拼在一起组成的。
有趣的是,1973年,在英国政府通讯总部工作的数学家克利福德·柯克斯(Clifford Cocks)在一个内部文件中提出了一个相同的算法,但他的发现被列入机密,一直到1997年才被发表。
-
RSA 非对称加密算法中离散对数难题的应用
回顾前面的 迪菲赫尔曼秘钥交换算法,其核心思想是使用单向函数对公开秘钥进行加密(离散对数就是一种典型的单向函数):
m e m o d n = c , e ∈ [ 1 , n − 1 ] , 其 中 模 数 n 为 质 数 , m 为 n 的 一 个 原 根 m^e~~mod~~ n~=~c~,~~e \in [1,n - 1]~,其中模数~n~为质数,m~为~n~的一个原根 me mod n = c , e∈[1,n−1] ,其中模数 n 为质数,m 为 n 的一个原根
在已知 m m m、 n n n、 c c c 的情况下,求解指数 e e e 只能采取试错法,求解指数 e e e 的过程构成单向函数。同样地, m e m o d n = c m^e~~mod~~ n~=~c~ me mod n = c 中,已知 e e e、 n n n、 c c c ,求解底数 m m m ,也只能采取试错法。即求解底数 m m m 的过程,同样构成单向函数。
迪菲赫尔曼秘钥交换算法 利用离散对数难题:
m e m o d n = c , e ∈ [ 1 , n − 1 ] , 其 中 模 数 n 为 质 数 , m 为 n 的 一 个 原 根 m^e~~mod~~ n~=~c~,~~e \in [1,n - 1]~,其中模数~n~为质数,m~为~n~的一个原根 me mod n = c , e∈[1,n−1] ,其中模数 n 为质数,m 为 n 的一个原根
求解指数 e e e 的过程构成单向函数RSA非对称加密算法 利用离散对数难题:
m e m o d n = c m^e~~mod~~ n~=~c~ me mod n = c
求解底数 m m m 的过程构成单向函数虽然 RSA非对称加密算法 和 迪菲赫尔曼秘钥交换算法 都是利用离散对数难题构成单向函数,但是两者使用离散对数难题的方式是不同的。
-
RSA 非对称加密算法的数学描述
下面公式中,用到的英文字母所代表的含义:
m:message,明文
c:ciphertext,密文
e:encryption,加密
d:decryption,解密
n:number,数字(这里代表的是两个大质数相乘所得的合数)考虑下面两个等式:
① m e m o d n ≡ c ~~m^e~~mod~~ n~\equiv~c~ me mod n ≡ c
② c d m o d n ≡ m ~~c^d~~mod~~ n~\equiv~m~ cd mod n ≡ m假设存在正整数 e e e、 d d d、 n n n 使得 等式① 和 等式② 同时成立,那么可以:
- 将 e e e 和 n n n 作为公钥进行发布,用于加密 m m m
- 将 d d d 和 n n n 作为私钥进行保留,用于解密 c c c
这样做的优点在于:
- 对于 等式① m e m o d n ≡ c ~~m^e~~mod~~ n~\equiv~c~ me mod n ≡ c ,在知道 e e e、 n n n、 c c c 的情况下,由于离散对数难题,难以通过 e e e、 n n n、 c c c 反算出 m m m ,保证了 m m m 在传递过程中的安全性。 m m m 即使在传递的过程中被截获,也难以被破解
- 对于等式② c d m o d n ≡ m ~~c^d~~mod~~ n~\equiv~m~ cd mod n ≡ m ,在知道 c c c、 n n n、 m m m 的情况下,由于离散对数难题,难以通过 c c c、 n n n、 m m m 反算出 d d d,保证了 d d d 在使用过程中的安全性。使用 等式① m e m o d n ≡ c ~~m^e~~mod~~ n~\equiv~c~ me mod n ≡ c 进行加密的人,难以通过其已知的 c c c、 n n n、 m m m 反算出 d d d
- 等式① 和 等式② 均为模幂运算,消息发送者(已知 e e e、 n n n)使用 等式① 加密消息、消息接受者(已知 d d d、 n n n)使用 等式② 解密消息,速度都很快
- 在 e e e、 d d d、 n n n 确定的情况下,任何通过 等式① 进行加密的 m m m,都可以通过 等式② 进行解密。这就意味着,任意消息发送者都可以使用同一个 等式① 与 同一个使用 等式② 的消息接受者通讯。消息接受者在所有通讯过程中,只需要维护一对 e e e、 d d d、 n n n。
综上所述,通过
① m e m o d n ≡ c ~~m^e~~mod~~ n~\equiv~c~ me mod n ≡ c
② c d m o d n ≡ m ~~c^d~~mod~~ n~\equiv~m~ cd mod n ≡ m
进行通讯过程的加密和解密,有诸多优点。
关键点在于找到合适且安全的 e e e、 d d d、 n n n,使得上述等式成立。为了使 e e e、 d d d、 n n n 之间的关系变得更加明确,我们对 等式② 进行变形得到 等式③:
c d m o d n ≡ m ~~~~~~c^d~~mod~~ n~\equiv~m~ cd mod n ≡ m
( m e m o d n ) d m o d n ≡ m ~~~~~~(m^e~~mod~~n)^d~~mod~~ n~\equiv~m~ (me mod n)d mod n ≡ m
m e d m o d n ≡ m ~~~~~~m^{ed}~~mod~~ n~\equiv~m~ med mod n ≡ m
③ m e d ≡ m m o d n ~~m^{ed}\equiv~m~~mod~~ n~ med≡ m mod n
接下来,我们对欧拉定理进行变形得到 等式④:
若 m m m, n n n 为正整数,且 m m m, n n n 互质,则有
m φ ( n ) ≡ 1 m o d n ~~~~~~m^{φ(n)}\equiv1~~mod~~n mφ(n)≡1 mod n
( m φ ( n ) ) k ≡ ( 1 m o d n ) k ~~~~~~{(m^{φ(n)})}^k\equiv{(1~~mod~~n)}^k (mφ(n))k≡(1 mod n)k
m k φ ( n ) ≡ 1 m o d n ~~~~~~m^{kφ(n)}\equiv1~~mod~~n mkφ(n)≡1 mod n
m k φ ( n ) × m ≡ 1 × m m o d n ~~~~~~m^{kφ(n)}~\times~m\equiv1~\times~m~~mod~~n mkφ(n) × m≡1 × m mod n
④ m k φ ( n ) + 1 ≡ m m o d n ~~m^{kφ(n)+1}\equiv~m~~mod~~n mkφ(n)+1≡ m mod n
对比 等式③ 和 等式④:
③ m e d ≡ m m o d n ~~m^{ed}\equiv~m~~mod~~ n~ med≡ m mod n
④ m k φ ( n ) + 1 ≡ m m o d n ~~m^{kφ(n)+1}\equiv~m~~mod~~n~~~ mkφ(n)+1≡ m mod n ( m m m, n n n 为正整数,且 m m m, n n n 互质)
我们发现:
在 m m m 和 n n n 为正整数且互质的前提下,只要让 e d ≡ k φ ( n ) + 1 ed\equiv~kφ(n)+1 ed≡ kφ(n)+1,等式③ m e d ≡ m m o d n ~~m^{ed}\equiv~m~~mod~~ n~ med≡ m mod n ,便会成立。即,在 m m m 和 n n n 互质的前提下,只要 e e e、 d d d、 n n n 满足: e d ≡ k φ ( n ) + 1 ed\equiv~kφ(n)+1 ed≡ kφ(n)+1,等式① 和 等式② 就会同时成立,此时,使用 等式①对 m m m 进行加密 、使用 等式② 对 c c c 进行解密,就是可行的。先别高兴,这里还存在两个问题:
- 根据 e d ≡ k φ ( n ) + 1 ed\equiv~kφ(n)+1 ed≡ kφ(n)+1,推出 d ≡ k φ ( n ) + 1 e d\equiv~\frac{kφ(n)+1}{e} d≡ ekφ(n)+1 ,又因为 e e e 和 n n n,作为公钥暴露在外面,如果有人算出了 φ ( n ) φ(n) φ(n),并对 k k k 进行枚举,可以很容易反算出 d d d
- 为了不让他人轻易算出 φ ( n ) φ(n) φ(n),我们可以取 n n n 为几百位的大整数,欧拉函数的结果本身就不好求,当 n n n 为几百位的大整数时, φ ( n ) φ(n) φ(n) 也相当于一个单向函数。但是,这样又造成了另外一个问题:我们在生成公钥和私钥的过程中,需要通过 φ ( n ) φ(n) φ(n) 确定 e e e 和 d d d 的值,如果 n n n 为几百位的大整数,我们自己也算不出 φ ( n ) φ(n) φ(n) 的值,那 e e e 和 d d d 就生成不了。
问题到这里,似乎陷入了死胡同,除非存在这么一种情况:存在一个条件,我们通过这个条件,很容易能算出 φ ( n ) φ(n) φ(n),不知道这个条件的人,很难算出 φ ( n ) φ(n) φ(n),只要我们把这个条件掌握在手里,不对外公布, φ ( n ) φ(n) φ(n) 就是安全的。
接下来,我们看欧拉函数的两个重要性质:
- 若 p p p 是质数,则有 φ ( p ) = p − 1 φ(p)=p-1 φ(p)=p−1
- 若 x x x, y y y 互质,则有 φ ( x y ) = φ ( x ) φ ( y ) φ(xy)=φ(x)φ(y) φ(xy)=φ(x)φ(y)
于是,我们取两个上百位的大质数 P 1 P_1 P1 和 P 2 P_2 P2,令 n = P 1 × P 2 n=P_1~\times~P_2 n=P1 × P2,则有:
φ ( n ) = φ ( P 1 P 2 ) = φ ( P 1 ) φ ( P 2 ) = ( P 1 − 1 ) ( P 2 − 1 ) φ(n)=φ(P_1P_2)=φ(P_1)φ(P_2)=(P_1-1)(P_2-1) φ(n)=φ(P1P2)=φ(P1)φ(P2)=(P1−1)(P2−1)
我们可以很容易地通过 P 1 P_1 P1 和 P 2 P_2 P2 求得 n n n 和 φ ( n ) φ(n) φ(n)。但是如果要将 n n n 因式分解为两个大质数 P 1 P_1 P1 和 P 2 P_2 P2,只能采取试错法进行枚举。即,大整数的质因数分解,构成一个单向函数。
上面对于 RSA 非对称加密算法的数学描述总体上已经完成,但是这里有个细节,需要注意:
我们在推导 e e e、 d d d、 n n n 关系的过程中用到了 欧拉定理
而使用 欧拉定理 的前提是: m m m 和 n n n 为正整数且互质
又因为 n = P 1 × P 2 n=P_1~\times~P_2 n=P1 × P2
所以 m m m 和 P 1 × P 2 P_1~\times~P_2 P1 × P2 也需要互质
因为 m m m 是通讯过程中产生的消息,所以不能对 m m m 的取值做过多的限定
为了抵消 欧拉定理 对于 m m m 取值的限制,需要 e e e、 d d d、 φ ( n ) φ(n) φ(n) 存在模反关系
更具体地,需要满足 d d d 为 e e e 关于 φ ( n ) φ(n) φ(n) 的模反元素,即:
e d m o d φ ( n ) ≡ 1 ed~~mod~~φ(n)\equiv1 ed mod φ(n)≡1在对 e e e、 d d d、 φ ( n ) φ(n) φ(n) 添加模反元素的约束后,欧拉定理 对于 m m m 和 n n n 互质的限制得到抵消。此时,只需要满足下面的两个条件,RSA 非对称加密算法就成立:
- m m m 和 n n n 为正整数并且 m < n m < n m<n
- d d d 为 e e e 关于 φ ( n ) φ(n) φ(n) 的模反元素(这其中隐含了一个条件: e e e 和 φ ( n ) φ(n) φ(n) 互质)
由条件 1 可以看出,RSA 不适用于加密过长的消息
-
RSA 非对称加密算法举例
上面 RSA 非对称加密算法的数学描述比较抽象,这里举个实例进行说明。
还是以上面 Alice 和 Bob 进行通讯,窃听者 Eve 进行窃听为情景:
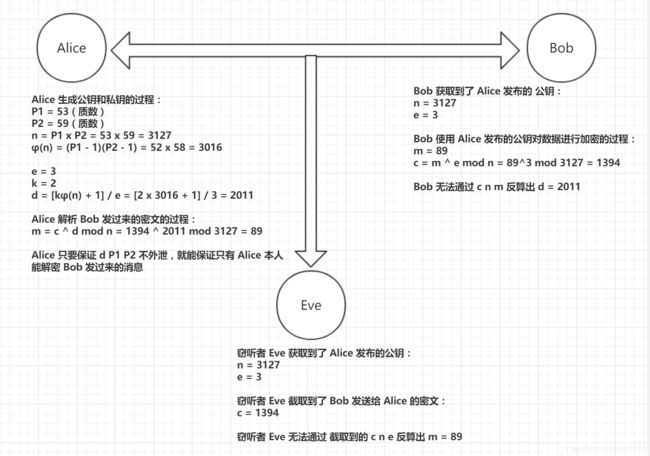
Alice 生成公钥和私钥的过程:- Alice 随机生成两个位数相当的质数 P 1 P_1 P1 和 P 1 P_1 P1,在这里: P 1 = 53 P_1=53 P1=53 、 P 2 = 59 P_2=59 P2=59
- Alice 通过 P 1 P_1 P1 和 P 1 P_1 P1 相乘,得到大整数 n n n,在这里: n = P 1 × P 2 = 53 × 59 = 3127 n=P_1~\times~P_2=53~\times~59=3127 n=P1 × P2=53 × 59=3127
- Alice 通过 P 1 P_1 P1 和 P 1 P_1 P1 计算出 φ ( n ) φ(n) φ(n),在这里: φ ( n ) = φ ( P 1 P 2 ) = φ ( P 1 ) φ ( P 2 ) = ( P 1 − 1 ) ( P 2 − 1 ) = 52 × 58 = 3016 φ(n)=φ(P_1P_2)=φ(P_1)φ(P_2)=(P_1-1)(P_2-1)=52~\times~58=3016 φ(n)=φ(P1P2)=φ(P1)φ(P2)=(P1−1)(P2−1)=52 × 58=3016
- Alice 选取系数 k k k 和 公开指数 e e e,在这里: k = 2 , e = 3 k=2~,~e=3 k=2 , e=3(因为 d d d 需要为 e e e 关于 φ ( n ) φ(n) φ(n) 的模反元素,所以公开指数 e e e 最好满足: e e e 为奇数并且 e e e 与 φ ( n ) φ(n) φ(n) 不具有公因数。因此,选取 e e e 为较小的奇质数,例如: 3 3 3、 5 5 5、 7 7 7、 11 11 11、…、 等最为合适。系数 k k k 可以随机选取一个正整数。)
- Alice 通过 k k k、 φ ( n ) φ(n) φ(n)、 e e e 计算出私有指数 d d d,在这里: d ≡ k φ ( n ) + 1 e = 2 × 3016 + 1 3 = 2011 d\equiv~\frac{kφ(n)+1}{e}=\frac{2~\times~3016+1}{3}=2011 d≡ ekφ(n)+1=32 × 3016+1=2011
- Alice 保存私钥 d d d、 n n n,发布公钥 e e e、 n n n,在这里: d = 2011 d=2011 d=2011、 e = 3 e=3 e=3、 n = 3127 n=3127 n=3127
Bob 加密数据的过程:
- Bob 获取到 Alice 发布的公钥 e e e 和 n n n,在这里: e = 3 e=3 e=3、 n = 3127 n=3127 n=3127
- Bob 生成要发送给 Alice 的明文 m m m,在这里: m = 89 m=89 m=89
- Bob 通过公钥 e e e 和 n n n 对明文 m m m 进行加密,在这里: c = m e m o d n = 8 9 3 m o d 3127 = 1394 c=~~m^e~~mod~~ n=~~89^3~~mod~~ 3127=1394 c= me mod n= 893 mod 3127=1394
- Bob 将密文发送给 Alice
- 由于 c d m o d n ≡ m c^d~~mod~~ n~\equiv~m~ cd mod n ≡ m 的单向性,Bob 无法通过 c c c、 n n n、 m m m 反算出 d d d
Alice 解析 Bob 发送过来的密文的过程:
- Alice 收到 Bob 发过来的密文 c c c,在这里: c = 1394 c=1394 c=1394
- Alice 通过私钥 d d d 和 n n n 对密文 c c c 进行解密,在这里: m = c d m o d n = 139 4 2011 m o d 3127 = 89 m=~~c^d~~mod~~ n~=~~1394^{2011}~~mod~~ 3127=89 m= cd mod n = 13942011 mod 3127=89
窃听者 Eve 能获取到的数据有:
- Alice 公布的公钥 e e e 和 n n n,在这里: e = 3 e=3 e=3、 n = 3127 n=3127 n=3127
- Bob 发送给 Alice 的密文 c c c,,在这里: c = 1394 c=1394 c=1394
- 由于 m e m o d n ≡ c m^e~~mod~~ n~\equiv~c~ me mod n ≡ c 的单向性,窃听者 Eve 无法通过 e e e、 n n n、 c c c 反算出 m m m
-
RSA 非对称加密算法总结
- RSA 非对称加密算法使用的是单向陷门函数,其求解 φ ( n ) φ(n) φ(n) 的过程,相当于在构造陷门
- RSA 的强度依赖于质因数分解的困难程度,这是质数分布这一深层次问题的结果,这个问题存在数千年,人类至今仍无法解决
- 由 RSA 的数学推导过程不难看出:
我们即可以使用公钥加密信息(加密 - encrypt)、私钥解密信息(解密 - decrypt)
也可以使用私钥加密信息(签名 - sign),公钥解密信息(验证 - verify) - RSA一般用于加密少量数据,在实际应用中,RSA 一般用于加密 对称加密算法的秘钥
- 因为:
RSA 单次能加密的数据量较小
RSA 加密过程使用的模幂运算相对于 对称加密 耗时较长
所以在实际运用中,一般是:
通讯双方使用 RSA 加密 对称加密算法 的秘钥
然后,通讯双方使用对称加密算法,加密实际通讯的数据