（二叉树）从中序和后序遍历构造树

题目描述

根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如，给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：
[3,9,20,null,null,15,7]

题目分析

对于树，只要给定树的中序遍历+前序遍历或者中序遍历+后序遍历结果，那么就一定能够构造出树的结构。如何构造呢？我们知道，前序遍历的第一个结点必定是根结点，后序遍历的最后一个结点一定是根结点，根据前序遍历或者后续遍历很容易就能找到根结点，如果树中不存在重复结点，那么在中序遍历中，根结点所在位置的左边就是左子树的中序遍历结果，右边就是右子树的中序遍历结果。什么意思呢？以给出的例子 中序遍历 inorder = [9,3,15,20,7]和后序遍历 postorder = [9,15,7,20,3]来分析：

由后序遍历可以知道根结点为3，再来到中序遍历中，那么3的左边和右边就分别是根结点的左子树和右子树的中序遍历结果，即根结点的左子树中序遍历为[9]，右子树中序遍历为[15,20,7]，很显然，根结点的左子树就只剩一个结点9了。

现在再来分析右子树：前面根据中序遍历可以知道，根结点的左子树上只有1个结点，右子树上有3个结点，结合后序遍历是左-右-根的特点，即后序遍历中必定是先遍历根结点的左子树，然后再是右子树，绝不会出现交叉的现象，因此在后序遍历结果中从左往右数1个，即是左子树的后序遍历结果，再接着数3个结点，即是右子树的后序遍历结果，最后剩下一个根结点，由此可以分析出：根结点为3，对于左子树：中序遍历为[9]，后序遍历为[9]；对于右子树，中序遍历为[15,20,7]，后序遍历为[15,7,20]，这样就可以分别得到左子树和右子树的中序和后序遍历结果，再如同上面分析即可。

那么现在来总结一下思路：

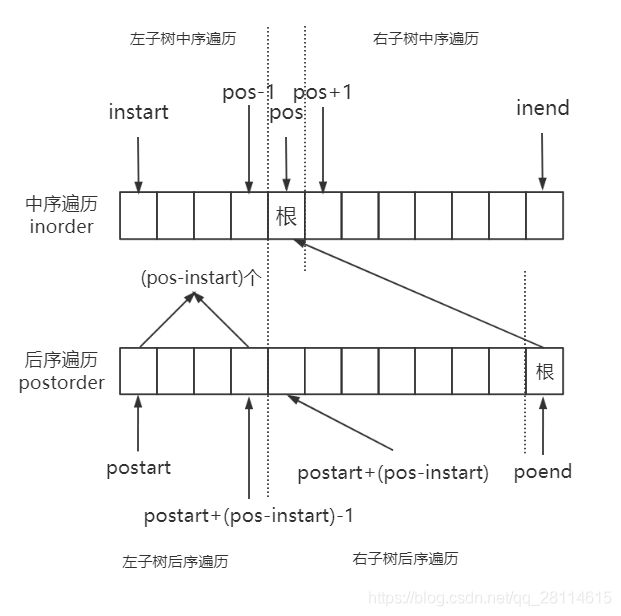
如图所示，先从后序遍历的末尾出发，找到中序遍历中根结点所在位置pos，那么instart ~ pos-1则是左子树的中序遍历，pos+1 ~ inend则是右子树的中序遍历，同样，postart ~ postart+pos-instart-1则是左子树的后序遍历，postart+pos-instart ~ poend-1则是右子树的后序遍历，这样，就最终找到左子树和右子树各自的的前序遍历和后序遍历，这样一直递归下去，将instart和pos-1作为左子树的instart和inend，pos+1和inend作为右子树的instart和inend；postart 和 postart+pos-instart-1作为左子树的postart和poend，postart+pos-instart和poend作为右子树的postart和poend，可见，instart和inend、postart和poend是在不断靠近的，直到instart>inend时，说明左子树为空，此时postart必定大于poend，递归停止，写出程序如下：

TreeNode* buildTree(vector& inorder, vector& postorder) {
        
        
        if(inorder.empty())return NULL;
        
        TreeNode * root=(TreeNode*)malloc(sizeof(TreeNode));
        
        int len=inorder.size();
        
        int pos=0;
        
        root->val=postorder[len-1];
        
        while(inorder[pos]!=root->val)pos++;
        root->left=build(inorder,postorder,0,pos-1,0,pos-1);
        root->right=build(inorder,postorder,pos+1,len-1,pos,len-2);
        
        return root;
    }
    TreeNode* build(vector& inorder, vector& postorder,int instart,int inend,int postart,int poend)
    {


        if(instart>inend)return NULL;
        
        TreeNode * root=(TreeNode*)malloc(sizeof(TreeNode));
        
        root->val=postorder[poend];
        
        int pos;
        for(pos=instart;pos<=inend;pos++)
            if(inorder[pos]==root->val)break;

        root->left=build(inorder,postorder,instart,pos-1,postart,pos-1-instart+postart);
        
        root->right=build(inorder,postorder,pos+1,inend,pos-instart+postart,poend-1);
        
        
        return root;
        
    }