【队列】队列 Queue(一):顺序队列与循环队列
背景
没什么背景,就是想研究下队列。
说明
顺序队列和循环队列的测试源码:
https://github.com/CherryXiuHuaWoo/Queue
什么是队列(Queue)?
队列在生活中可谓是无处不在。最常见的就是去超市买菜称重时大妈们排得贼长的队列(这是理想情况,通常是围成一圈),还有超市结账的队伍,还有以前食堂打饭的队伍。是不是很有印象呢~~~

那队列有什么特点呢?
就拿食堂打饭来说,下课铃声一响,千万大军冲向食堂,为的是早来早打上饭,晚来了,那队伍忒长了,想死的心都有了~~~为什么会这样子呢?队列有个原则叫做先进先出。先来排队的人先打饭,后来的人后打饭。比如说,队列 A 有 3 个人:A1,A2,A3。A1 是排第 1 个,A2 是排第 2 个,A3 是排第 3 个。那么,先打上饭的是 A1; A1 打完饭后,退出队列,到 A2 打饭;A2 打完饭后,退出队列,到 A3 打饭。如果在 A1,A2,A3 打饭期间,没有人来排队,等到 A3 打完饭后,队列就空了,我们称没有元素的队列为空队。因为我们每一个排队的人都遵守着“先进先出”的原则,才有了有序而浩荡的打饭大军队伍。
前面对打饭大军的介绍,我们对队伍有了初步的认识。下面将要用专业地描述队列。
队列的定义
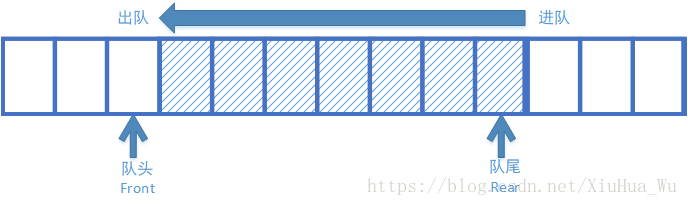
队列(Queue),简称:队,是一种只允许在表的一端进行插入操作,而在表的另外一端进行删除操作的线性表。
关于队列的基本概念:
- 队尾(rear):允许进行插入的一端
- 队头(front):允许进行删除的一端
- 进队:队列的插入操作
- 出队:队列的删除操作
- 原则:先进先出(First In First Out,FIFO)
队列的基本操作
- 队列的初始化。
- 进队:在队列的尾部插入一个新的元素。Ps:进队将改变队尾指针的位置。
- 出队:删队列的队头元素。Ps:出队将改变队头指针的位置。
- 测试队列是否为空。Ps:在队列删除操作前必须进行本操作。
- 测试队列是否已满。Ps:本操作通常只是在队列采用顺序存储结构时对队列插入操作之前要进行的一个操作。
- 取当前队头的元素。Ps:本操作不修改队头元素指针的位置。
队列的存储结构
一般来说,队列有两种存储结构:顺序存储结构和链式存储结构。
顺序队列
我们把采用顺序存储结构的队列简称为:顺序队列。
在实际的程序设计中,通常使用数组来描述队列的顺序存储结构:
- 定义一维数组 QUEUE[0…M-1] 来存放队列的元素。
- 定义整型变量 front 指出队头元素的位置。
- 定义整型变量 rear 指出队尾元素的位置。
NOTE
为了算法设计的方便以及算法本身的简单,我们约定:
- 队头指针 front 指出实际队头元素所在位置的前一个位置。
- 队尾指针 rear 指出实际队尾元素所在的位置。
下面,咱们以图例的方式介绍队列的变化过程。
1.顺序队列的定义
#define QUEUE_LENGTH 1000 /*定义队列的最大容量*/
QElemType Queue[QUEUE_LENGTH];
int front,rear;
PS:
ElemType 就是“数据元素的类型”,是一个抽象的概念,是表示我们所要使用的数据元素应有的类型。
2.顺序队列的初始状态
初始化时,队列为空,有 front = rear = -1。
3.元素 a1 进队后的状态
元素 a1 从队尾进队,rear = 0。
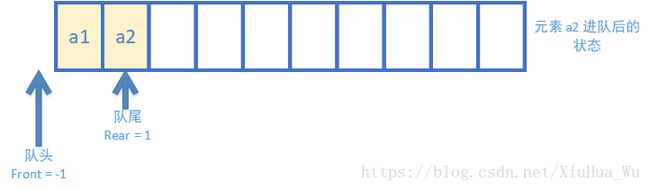
4.元素 a2 进队后的状态
元素 a2 从队尾进队,rear = 1。
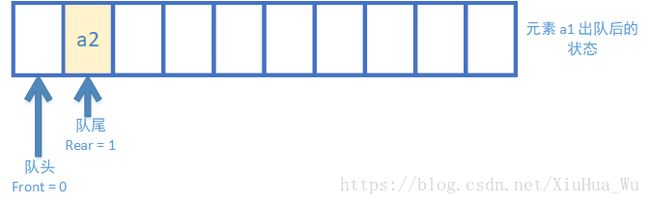
5.元素 a1 出队后的状态
元素 a1 从队头出队,front = 0。
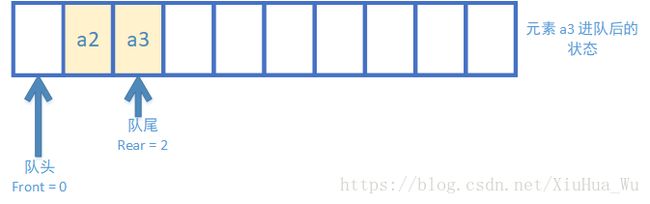
6.元素 a3 进队后的状态
元素 a3 从队尾进队,rear = 2。
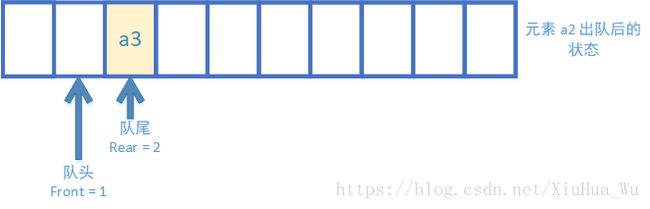
7.元素 a2 出队后的状态
元素 a2 从队头出队,front = 1。
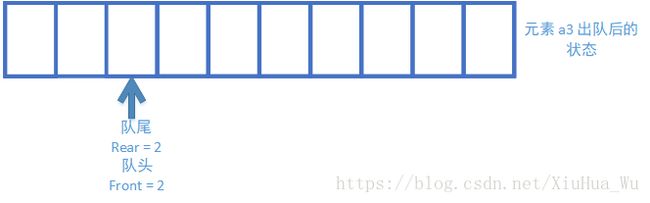
8.元素 a3 出队后的状态
元素 a3 从队头出队, front = 2。此时,队列已无元素,队列为空。
NOTE
在队列的设计过程中,我们需要考虑如下的异常情况。
- 非空队列随着删除操作的进行,队列可能为空。由上面的例程可知,队列为空的条件为 front = rear。
- 顺序队列有可能出现溢出问题。当队列已满时进行进队操作,这种现象称为:上溢。当队列已空时进行出队操作,这种现象称为:下溢。
顺序队列的基本算法
- 队列的初始化
- 测试队列是否为空
- 测试队列是否为满
- 取当前队头的元素
- 队列的插入(进队)
- 队列的删除(出队)
队列的初始化
/*
Function: Init Quueue
Intput:
Queue, ptr to Queue
Return: None
*/
void Queue_Init(QueueType *Queue)
{
memset(Queue->Queue, 0, sizeof(Queue->Queue)/sizeof(QElemType));
Queue->front = -1;
Queue->rear = -1;
}
测试队列是否为空
/*
Function: Empty Queue?
Intput:
Queue, ptr to Queue
Return:
Queue_EMPTY
Queue_OK
*/
static Queue_Status Queue_IsEmpty(QueueType *Queue)
{
if (Queue->front == Queue->rear)
{
QueuePrintf("Err: Queue is empty!\r\n");
return Queue_EMPTY;
}
else
{
return Queue_OK;
}
}
测试队列是否为满
/*
Function: Full Queue?
Intput:
Queue, ptr to Queue
Return:
Queue_FULL
Queue_OK
*/
static Queue_Status Queue_IsFull(QueueType *Queue)
{
if (Queue->rear == (QueueLength - 1))
{
QueuePrintf("Err: Queue is full!\r\n");
return Queue_FULL;
}
else
{
return Queue_OK;
}
}
取当前队头的元素
/*
Function: get element from queue
Intput:
Queue, ptr to Queue
item
Return:
Queue_EMPTY
Queue_OK
Other:
Don't change the front of Queue
*/
int Queue_GetElement(QueueType *Queue, QElemType &item)
{
// If Queue is empty, return Queue_EMPTY
if (Queue_EMPTY == Queue_IsEmpty(Queue))
{
return Queue_EMPTY;
}
else
{ // else get the item from Queue
item = Queue->Queue[Queue->front];
return Queue_OK;
}
}
队列的插入(进队)
/*
Function: add element into queue
Intput:
Queue, ptr to Queue
item
Return:
Queue_FULL
Queue_OK
*/
int Queue_AddElement(QueueType *Queue, QElemType &item)
{
// If Queue is full, return Queue_FULL
if (Queue_FULL == Queue_IsFull(Queue))
{
return Queue_FULL;
}
else
{ // else add the item into Queue
Queue->Queue[++Queue->rear] = item;
return Queue_OK;
}
}
队列的删除(出队)
/*
Function: delete element into queue
Intput:
Queue, ptr to Queue
item
Return:
Queue_EMPTY
Queue_OK
*/
int Queue_DeleteElement(QueueType *Queue, QElemType &item)
{
// If Queue is empty, return Queue_EMPTY
if (Queue_EMPTY == Queue_IsEmpty(Queue))
{
return Queue_EMPTY;
}
else
{ // else delete the item into Queue
item = Queue->Queue[++Queue->front];
return Queue_OK;
}
}
顺序队列的弊端
由代码和图例可以看出,顺序队列的 Queue_AddElement 中,当 rear随着入队累加,有可能出现 rear = QueueLength -1,导致在此时进行插入操作会返回溢出错误,队列的动态变化在向右偏移,我们把这种溢出称为“假溢出”。这并不是我们所期望的。由此引申出“循环队列”的概念,下面看怎么通过循环队列解决顺序队列的问题。
循环队列
如果把队列设想成头尾相连的循环表,使得空间可以循环利用,问题迎刃而解。
在进行插入操作时,当队列的第 M - 1 个元素被占用以后,只要队列前面还有可用空间,新的元素就可以从第 0 个位置开始加入队列。那么入队函数可以改为:
/*
Function: add element into queue
Intput:
Queue, ptr to Queue
item
Return:
Queue_FULL
Queue_OK
*/
int Queue_AddElement(QueueType *Queue, QElemType &item)
{
// If Queue is full, return Queue_FULL
if (Queue_FULL == Queue_IsFull(Queue))
{
return Queue_FULL;
}
else
{ // else add the item into Queue
Queue->rear = (Queue->rear + 1) % QueueLength;
Queue->Queue[Queue->rear] = item;
return Queue_OK;
}
}
出队函数改为:
/*
Function: delete element into queue
Intput:
Queue, ptr to Queue
item
Return:
Queue_EMPTY
Queue_OK
*/
int Queue_DeleteElement(QueueType *Queue, QElemType &item)
{
// If Queue is empty, return Queue_EMPTY
if (Queue_EMPTY == Queue_IsEmpty(Queue))
{
return Queue_EMPTY;
}
else
{ // else delete the item into Queue
Queue->front = (Queue->front + 1) % QueueLength;
item = Queue->Queue[Queue->front];
return Queue_OK;
}
}
而且,对于队列是否为 Empty 和 Full 的标准也随之改变:
/*
Function: Full Queue?
Intput:
Queue, ptr to Queue
Return:
Queue_FULL
Queue_OK
*/
static Queue_Status Queue_IsFull(QueueType *Queue)
{
if (((Queue->rear + 1)%QueueLength) == Queue->front)
{
QueuePrintf("Err: Queue is full!\r\n");
return Queue_FULL;
}
else
{
return Queue_OK;
}
}
/*
Function: Empty Queue?
Intput:
Queue, ptr to Queue
Return:
Queue_EMPTY
Queue_OK
*/
static Queue_Status Queue_IsEmpty(QueueType *Queue)
{
if (Queue->front == Queue->rear)
{
QueuePrintf("Err: Queue is empty!\r\n");
return Queue_EMPTY;
}
else
{
return Queue_OK;
}
}