状压DP入门
状压DP:
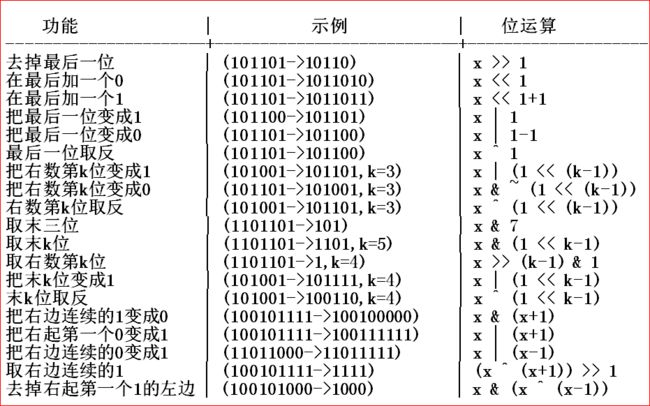
神奇的DP方式,简单来说就是用二进制来简单压缩状态,然后根据题目可能会有一点点改变。
但是不一定是用二进制,还有一些以压缩状态为思想的题目。
首先参考:
https://blog.csdn.net/Stockholm_Sun/article/details/78213290
http://www.cnblogs.com/Ronald-MOK1426/p/8451875.html
https://blog.csdn.net/qq_36183935/article/details/70904217
https://www.cnblogs.com/Ronald-MOK1426/p/8456945.html
比较重要的状态转移和状态判断。
第一道题 洛谷
P1879 入门题 Corn Fields
Description
Farmer John has purchased a lush new rectangular pasture composed of M by N (1 ≤ M ≤ 12; 1 ≤ N ≤ 12) square parcels. He wants to grow some yummy corn for the cows on a number of squares. Regrettably, some of the squares are infertile and can't be planted. Canny FJ knows that the cows dislike eating close to each other, so when choosing which squares to plant, he avoids choosing squares that are adjacent; no two chosen squares share an edge. He has not yet made the final choice as to which squares to plant.
Being a very open-minded man, Farmer John wants to consider all possible options for how to choose the squares for planting. He is so open-minded that he considers choosing no squares as a valid option! Please help Farmer John determine the number of ways he can choose the squares to plant.
Input
Line 1: Two space-separated integers:M and N
Lines 2..M+1: Line i+1 describes row i of the pasture with N space-separated integers indicating whether a square is fertile (1 for fertile, 0 for infertile)
Output
Line 1: One integer: the number of ways that FJ can choose the squares modulo 100,000,000.
Sample Input
2 3
1 1 1
0 1 0
Sample Output
9
Hint
Number the squares as follows:
1 2 3
4
There are four ways to plant only on one squares (1, 2, 3, or 4), three ways to plant on two squares (13, 14, or 34), 1 way to plant on three squares (134), and one way to plant on no squares. 4+3+1+1=9.
用二进制存储状态去用上面的各种位运算用于判断,预处理所有状态然后把这些状态依次放进去首先判断满足不相邻条件,再判断是否会与上面相邻,并且用上面的进行转移。
#include
#include
#include
#include
#include 第二道题
http://www.cnblogs.com/Ronald-MOK1426/p/8456798.html
【洛谷P1896【SCOI2005】】互不侵犯King
题目描述
在N×N的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共8个格子。
输入输出格式
输入格式:
只有一行,包含两个数N,K ( 1 <=N <=9, 0 <= K <= N * N)
输出格式:
所得的方案数
输入输出样例
输入样例#1:
3 2
输出样例#1:
16
解题方法差不多也是转移从上一行下来的01串,就是判断是否满足条件多了左上左下等而已。
事实上,中间有一步我处理重复0的情况不加也能AC,不知道为什么。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
P2704 [NOI2001]炮兵阵地
基础偏一点处理
处理两行的状态,因为需要考虑判断的是左两个(预处理状态的时候就可以排除),还有上面两个,需要存下相邻两行状态,然后递推就可以也满足右下,相当于之后的左上。
然后动规方程:dp[第i行][第i行状态][第i-1行状态]=max(dp[i][i状态][i-1状态],dp[i-1][i-1状态][i-2状态]+i状态炮兵数目)
然后第几行需要作为滚动数组,防止MLE,因为其实动规方程递推的时候只需要考虑前一行就可以,dp[2][1<<10+1][1<<10+1]的容量就已经完全满足了。
细节判定条件和之前基本一致。本题貌似单字符处理会WA,有些玄学,反正我处理这道题花了很久,明明基本都写出来了,都困在字符串处理上,用cin gets getchar 效果有时候居然不同。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include 入门剩余题:
UESTC 数据结构专题一道状压DP
洛谷— —过河:扩展欧几里得+离散化(有点难)