二叉树——根据先序（后序）和中序遍历建树

假设有棵树，长下面这个样子，它的前序遍历，中序遍历，后续遍历都很容易知道。

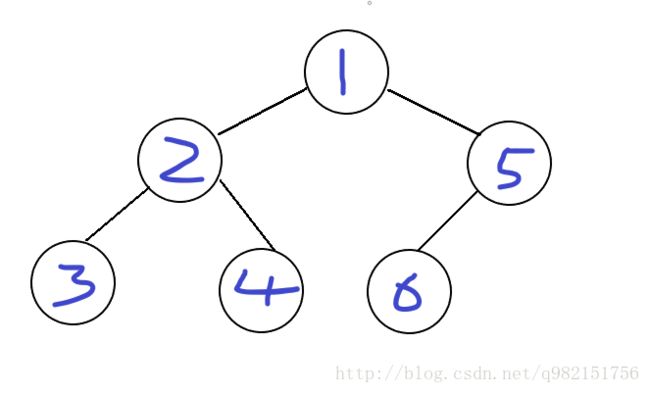
PreOrder: 1, 2, 3, 4, 5, 6
InOrder: 3, 2, 4, 1, 6, 5
PostOrder: 3, 4, 2, 6, 5, 1
现在，假设仅仅知道前序和中序遍历，如何求后序遍历呢？或者只知道后序和中序遍历，如何求前序遍历呢？（因为这两种情况的差别不大，所以只讲一种）

第一步，root最简单，前序遍历的第一节点“1”就是root。

第二步，继续观察前序遍历“1, 2, 3, 4, 5, 6”，除了知道“1”是root，剩下的节点必然是root的左右子树之外，没法找到更多信息了。

第三步，那就观察中序遍历“ 3, 2, 4, 1, 6, 5”。其中root节点“1”左侧的“3, 2, 4”必然是root的左子树，“1”右侧的“6, 5”必然是root的右子树。

第四步，观察左子树“3, 2, 4”，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为“2”。

第五步，同样的道理，root的右子树节点“6，5”中的根节点也可以通过前序遍历求得。在前序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的右子树的第一个节点就是右子树的根节点。
如何知道哪里是前序遍历中的左子树和右子树的分界线呢？通过中序遍历去数节点的个数。
在上一次中序遍历中，root左侧是“3，2，4”，所以有3个节点位于root左侧。那么在前序遍历中，必然是第1个是“1”，第2到第4个由“2，3，4”构成，第5个就是root的右子树的根节点了，是“5”。

第六步，观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。

代码：

import java.util.LinkedList;
import java.util.Queue;
class Node {
    int value;
    Node left = null;
    Node right = null;
}
public class CreatTree {
    static int pre[] = {1, 2, 3, 4, 5, 6};
    static int post[] = {3, 4, 2, 6, 5, 1};
    static int in[] = {3, 2, 4, 1, 6, 5};
    static int cnt1 = 0, cnt2 = post.length - 1;
    public static Node creatTreeByPreAndIn(int start, int end) {
        if(start > end) return null;
        int root = pre[cnt1];
        cnt1++;
        int rootindex = findIndex(in, root);
        Node t = new Node();
        t.value = root;
        if(start == end) {
            t.left = t.right = null;
        }
        else {
            t.left = creatTreeByPreAndIn(start, rootindex - 1);
            t.right = creatTreeByPreAndIn(rootindex + 1, end);
        }
        return t;
    }
    public static Node creatTreeByPostAndIn(int start, int end) {
        if(start > end) return null;
        int root = post[cnt2];
        cnt2--;
        int rootindex = findIndex(in, root);
        Node t = new Node();
        t.value = root;
        if(start == end) {
            t.left = t.right = null;
        }
        else {
            t.right = creatTreeByPostAndIn(rootindex + 1, end);
            t.left = creatTreeByPostAndIn(start, rootindex - 1);
        }
        return t;
    }
    public static int findIndex(int[] a, int b) {
        int i = 0;
        for(i=0;iif(a[i] == b) {
                return i;
            }
        }
        return -1;
    }
    public static void Show(Node root) {
        Queue q = new LinkedList<>();
        q.offer(root);
        while(!q.isEmpty()) {
            Node temp = q.poll();
            System.out.printf("%d ",temp.value);
            if(temp.left != null) {
                q.offer(temp.left);
            }
            if(temp.right != null) {
                q.offer(temp.right);
            }
        }
        System.out.println();
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int start = 0;
        int end = in.length - 1;
        Node head = creatTreeByPreAndIn(start, end);
        Show(head);
        Node head2 = creatTreeByPostAndIn(start, end);
        Show(head2);
    }
}