Top-k高效用项集挖掘_学习笔记(三) TKO

前言

本篇博客出于学习交流目的，主要是用来记录自己学习后的理解，过程中遇到的问题和心路历程，方便之后回顾。过程中可能引用其他大牛的博客，文末会给出相应链接，侵删！

REMARK：本人菜鸟一枚，如有理解错误还望大家能够指出，相互交流。也是第一次以博客的形式记录，文笔烂到自己都看不下去，哈哈哈

---

这篇学习笔记关于一种高效Top-k的频繁效用项集挖掘算法。
参考文献：Efficient Algorithms for Mining Top-K High Utility Itemsets

本篇博客介绍论文中的第二种 one-phase算法TKO，一些必要的基础概念和定义在Top-k高效用项集挖掘学习笔记(一) 基础概念中给出，另一种 two-phase 算法在 Top-k高效用项集挖掘学习笔记(二) TKU 中详细记录，请手动跳转。

正文

TKO算法是这篇文章提出的第二种算法，他只需要一个过程就可以得到结果。这个算法基于HUI-Miner算法以及它的utility-list 结构，TKO的项集从这个utility-list中生成而不扫描原始数据库。本篇结构还是先说基础算法 TKOBase T K O B a s e ，然后再说最终版本，即在基础算法上加优化策略。（算法中包括 RUC、RUZ、EPB R U C 、 R U Z 、 E P B 优化策略）

utility-list 结构

开始算法前，先简单了解一下utility-list 结构。

项的utility-list 被称作 initial utility-lists，可以通过扫描两次数据库得到。第一次遍历时计算项的TWU值和效用值；第二次扫描数据库时每个交易记录中的项按TWU值大小排序，并且每个项的 utility-list 被创建。

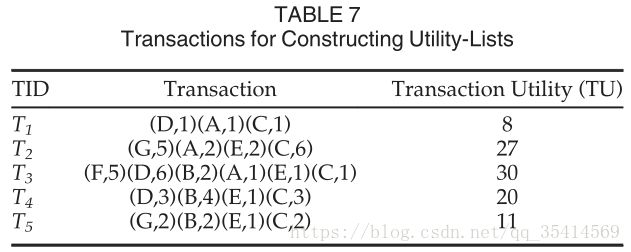
如表7所示，即交易记录中item按TWU值从小到大排序后的结果。

Fig.4展示了各项的utility-lists。每个item都由一个或多个元组组成，即有哪些交易记录包含这些项；元组由三部分组成（Tid，内部效用值iutil，剩余效用值rutil）；剩余效用值就是这个item后面的效用值之和，具体看下面的定义。

Definition 17. 前驱和后继(Precede and succeed)：
按照TWU值从小到大排列项， Ii≺Ij I i ≺ I j 表示 Ii I i 在 Ij I j 之前，即前驱，当且仅当 TWU(Ii) T W U ( I i ) 大于或等于 TWU(Ij) T W U ( I j ) ，并且 Ii I i 按字典序比 Ij I j 小；否则称为后继，记作 Ii≻Ij I i ≻ I j (原文符号标记好像有误)。

Definition 18. 项集的级联(Concatenation of an itemset)：
有两个项集 X={x1,x2,⋯,xu}(xi∈I∗,1≤i≤u) X = { x 1 , x 2 , ⋯ , x u } ( x i ∈ I ∗ , 1 ≤ i ≤ u ) 和 Y={y1,y2,⋯,yv}(yj∈I∗,1≤j≤v) Y = { y 1 , y 2 , ⋯ , y v } ( y j ∈ I ∗ , 1 ≤ j ≤ v ) ，当且仅当 X⊂Y X ⊂ Y 并且 Y Y 的每个 item yi∉X y i ∉ X 都是X所有 item 的后继， Y Y 称为 X X 的级联。

Definition 19. (Appear after)：
给定优先集合 I∗={I1,I2,⋯,Im} I ∗ = { I 1 , I 2 , ⋯ , I m } ，和顺序 I1≺I2≺⋯≺Im I 1 ≺ I 2 ≺ ⋯ ≺ I m ；假设项集和交易记录中的项都按这个顺序排序好了，在一个交易记录 Tr T r 中，一个项 Ij∈I∗ I j ∈ I ∗ 在项集 X={x1,x2,⋯,xL} X = { x 1 , x 2 , ⋯ , x L } 之后发生，当且仅当 Ij∈Tr I j ∈ T r 并且 x1≺x2≺⋯≺xL≺Ij x 1 ≺ x 2 ≺ ⋯ ≺ x L ≺ I j ； Tr T r 中所有出现在 X X 之后的项集记作 Tr/X T r / X 。

Definition 20. 交易记录剩余效用值(Remaining utility of an itemset in a transaction)： RU(X,Tr) R U ( X , T r )

RU(X,Tr)=∑Ii∈Tr/XEU(Ii,Tr) R U ( X , T r ) = ∑ I i ∈ T r / X E U ( I i , T r )

Definition 21. 数据库中的剩余效用值(Remaining utility of an itemset in a database)： RU(X) R U ( X )

RU(X)=∑Tr∈DRU(X,Tr) R U ( X ) = ∑ T r ∈ D R U ( X , T r )

Definition 22. 效用列表结构(Utility-list structure)： ul(X) u l ( X )
项集X的Utility-list记作 ul(X) u l ( X ) ，里头存着若干三元组，有几个交易记录包含该项集就有几个元组，每个元组 ⟨r,EU(X,Tr),RU(X,Tr)⟩ ⟨ r , E U ( X , T r ) , R U ( X , T r ) ⟩ ，即交易记录的序号，X在交易记录上的效用值，X在交易记录上的剩余效用值。

以表7的数据集为例， {D} { D } 在 T1 T 1 上的剩余效用值 RU({D},T1)=EU({A},T1)+EU({C},T1) R U ( { D } , T 1 ) = E U ( { A } , T 1 ) + E U ( { C } , T 1 ) ； {D} { D } 在整个数据集上的剩余效用值 RU({D})=RU({D},T1)+RU({D},T3)+RU({D},T4)=（6+13+14）=33 R U ( { D } ) = R U ( { D } , T 1 ) + R U ( { D } , T 3 ) + R U ( { D } , T 4 ) = （ 6 + 13 + 14 ） = 33 ； {DE} { D E } 在整个数据集上的剩余效用值 RU({DE})=RU({DE},T3)+RU({DE},T4)=（1+3）=4 R U ( { D E } ) = R U ( { D E } , T 3 ) + R U ( { D E } , T 4 ) = （ 1 + 3 ） = 4 。

Property 4.在项集X的Utility-list中，所有元组第二列（ iutil i u t i l ）的结果相加即X的效用值。

Property 5.有项集 X X 和级联项集 Y⊃X Y ⊃ X ，如果把元组第二列（ iutil i u t i l ）和第三列（ rutil r u t i l ）全部求和的效用值小于阈值 δ δ ，那么 Y Y 的效用值也小于 δ δ 。

Y Y 是 X X 级联，根据定义18， Y Y 中多的项一定排在 X X 之后，而 X X 的 iutil i u t i l 和 rutil r u t i l 的累加和一定大于等于 Y Y 的 iutil i u t i l 和 rutil r u t i l 的累加和，根据 Property 4 P r o p e r t y   4 所以一定大于Y的效用值。

TKOBase T K O B a s e 算法——基础算法

TKOBase T K O B a s e 输入参数k和一个数据集 D D ； TKOBase T K O B a s e 开始时设置 min_utilBorder=0 m i n _ u t i l B o r d e r = 0 ，并且创建一个小堆结构 TopK−CI−List T o p K − C I − L i s t 来存储过程中的top-k HUIs H U I s ;算法扫描两边数据库创建initial utility-lists ϕ−ULs ϕ − U L s ；然后用Topk-HUI-Search 算法（基于结合RUC：Raising threshold byUtility of Candidates和HUI-Miner算法，出自参考论文14）去挖掘搜索空间中的top-k HUI；算法不断更新 TopK−CI−List T o p K − C I − L i s t 中的top-k HUIs H U I s ，并利用列表中的信息更新 min_utilBorder m i n _ u t i l B o r d e r ；算法结束时， TopK−CI−List T o p K − C I − L i s t 中保存的即为top-k HUIs H U I s 完整解集。

对于每个搜索过程产生的L-项集 X={x1,x2,⋯,xL} X = { x 1 , x 2 , ⋯ , x L } ，如果都不小于 min_utilBorder m i n _ u t i l B o r d e r ，那么利用RUC策略来更新 min_utilBorder m i n _ u t i l B o r d e r 的值。RUC就是把X加入 TopK−CI−List T o p K − C I − L i s t 中，然后 min_utilBorder m i n _ u t i l B o r d e r 更新为第k大EU值项集的阈值，把低于 min_utilBorder m i n _ u t i l B o r d e r 的项集从 TopK−CI−List T o p K − C I − L i s t 中删去，保证 TopK−CI−List T o p K − C I − L i s t 中只有top-k个。

算法伪代码如下图所示：

比较项集 X X 的 iutil i u t i l 和 rutil r u t i l 的累加和与 min_utilBorder m i n _ u t i l B o r d e r 大小，利用Property 5剪枝（第六行）； Class[X] C l a s s [ X ] 和 ULS[X] U L S [ X ] 分别储存项集级联以及他们的 utility-lists（第七行）；候选项集 Z=X∪Y Z = X ∪ Y ，并创建Z的utility-lists ul(Z) u l ( Z ) ，之后就是不断迭代的过程，直到没有候选项集生成时停止。

策略6：RUC（Raising the threshold by the Utilities of Can-didates）
这个策略可以用于任何one-phace依赖效用值建立的算法。该策略用 TopK−CI−List T o p K − C I − L i s t 结构保存top-k HUIs H U I s ，并把项集按降序排列。最初 TopK−CI−List T o p K − C I − L i s t 为空，把新项集X加入 TopK−CI−List T o p K − C I − L i s t 中，然后 min_utilBorder m i n _ u t i l B o r d e r 更新为第k大EU值项集的阈值，把低于 min_utilBorder m i n _ u t i l B o r d e r 的项集从 TopK−CI−List T o p K − C I − L i s t 中删去，保证 TopK−CI−List T o p K − C I − L i s t 中只有top-k个。

当给定两个项集 X X 和 Y Y 以及他们的前缀 P P ，在Topk-HUI-Search 算法过程中，项集 Z=X∪Y Z = X ∪ Y 的utility-lists ul(Z) u l ( Z ) 由下结构过程生成，其中包括两种情况：

CAES1：假设有一项集 X={x1} X = { x 1 } 和 Y={y1} Y = { y 1 } ，并且 x1≺y1 x 1 ≺ y 1 。让 Z=X∪Y={x1，y1} Z = X ∪ Y = { x 1 ， y 1 } 是由X级联 y1 y 1 生成的二项集。utility-lists ul(X) u l ( X ) 和utility-lists ul(Y) u l ( Y ) 初始化的时候就被创建了，而utility-lists ul(Z) u l ( Z ) 是通过下面的方法得到。包含项集Z的交易记录记为 Tr T r ，在utility-lists ul(Z) u l ( Z ) 中创建元组 ⟨Tr,EU(Z,Tr),RU(Z,Tr)⟩ ⟨ T r , E U ( Z , T r ) , R U ( Z , T r ) ⟩ ，其中 EU(Z,Tr)=EU(x1,Tr)+EU(y1,Tr) E U ( Z , T r ) = E U ( x 1 , T r ) + E U ( y 1 , T r ) ， RU(Z,Tr)=EU(y1,Tr) R U ( Z , T r ) = E U ( y 1 , T r )

CAES2：假设有L-1项集 X={x1，x2，⋯，xL−1} X = { x 1 ， x 2 ， ⋯ ， x L − 1 } 和 Y={y1，y2，⋯，yL−1} Y = { y 1 ， y 2 ， ⋯ ， y L − 1 } （ L≥2 L ≥ 2 ），有 xi=yi(1≤i≤L−1) x i = y i ( 1 ≤ i ≤ L − 1 ) 以及 xL−1≺yL−1 x L − 1 ≺ y L − 1 。让 Z=X∪Y={x1，x2，⋯，xL−1，yL−1} Z = X ∪ Y = { x 1 ， x 2 ， ⋯ ， x L − 1 ， y L − 1 } 是由X级联 yL−1 y L − 1 生成的L项集；让 P=X∩Y={x1，x2，⋯，xL−2} P = X ∩ Y = { x 1 ， x 2 ， ⋯ ， x L − 2 } 是 X X 和 Y Y 的共同前缀，给出utility-lists ul(X) u l ( X ) ， ul(Y) u l ( Y ) 和 ul(P) u l ( P ) ，而utility-lists ul(Z) u l ( Z ) 是通过下面的方法得到。
包含项集Z的交易记录记为 Tr T r ，在utility-lists ul(Z) u l ( Z ) 中创建元组 ⟨Tr,EU(Z,Tr),RU(Z,Tr)⟩ ⟨ T r , E U ( Z , T r ) , R U ( Z , T r ) ⟩ ，其中 EU(Z,Tr)=[EU(X,Tr)+EU(Y,Tr)]−EU(P,Tr) E U ( Z , T r ) = [ E U ( X , T r ) + E U ( Y , T r ) ] − E U ( P , T r ) ， RU(Z,Tr)=EU(Y,Tr) R U ( Z , T r ) = E U ( Y , T r ) 。

TKO T K O 算法——最终算法

将给出四种改进策略用于 TKOBase T K O B a s e 算法就是 TKO T K O 算法，前两种是PE和DGU，这两个在前一个算法里以及说明了。下面说另外两种改进策略。

Definition 23. (Z-element)：当一个元素的剩余效用值是0的时候被称为Z-element，否则被称为NZ-element。在X的效用列表中的所有Z-element集合记作 ZE(X) Z E ( X ) 。

例如， {DBC} { D B C } 有两个Z-element， ZE({DBC})={⟨T3,17,0⟩,⟨T4,17,0⟩} Z E ( { D B C } ) = { ⟨ T 3 , 17 , 0 ⟩ , ⟨ T 4 , 17 , 0 ⟩ } 。

Property 6. NZEU(X) N Z E U ( X ) 是项集 X X 的所有NZ-element的第二列（iutil）的和，如果 [NZEU(X)+RU(X)]<min_utilBorder [ N Z E U ( X ) + R U ( X ) ] < m i n _ u t i l B o r d e r ，那么所有项集 X X 的级联都不是top-k HUIs。

策略7：RUZ（Reducing estimated utility values by using Z-elements）
该策略用在用于Topk-HUI-Search 算法生成候选项集过程中，根据Property 6，我们没必要生成 [NZEU(X)+RU(X)] [ N Z E U ( X ) + R U ( X ) ] 小于 min_utilBorder m i n _ u t i l B o r d e r 的项。

策略8：EPB（Exploring the most Promising Branches first）
该策略的目标是优先生成那些高效用值的候选项集，利用思想总是先扩展拥有最高预计效用值的项，这样更可能得到高效用值，因为这样可以更早的提早 min_utilBorder m i n _ u t i l B o r d e r ，就可以剪枝更多的搜索空间。

总结

作者在多个不同稀疏程度的数据集上作了对比，对比 TKO T K O 和 TKU T K U 算法，总体上TKO} TKO} 效果要好，包括内存消耗和速度上，因为 TKO T K O 是one-phace算法，具体详细对比可以看原文。

这篇文章看起来内容很多，但是如果把定义都理解清楚还是容易看懂的，最后几乎快变成翻译这篇论文了，不过我已经尽量简化一些复杂的定义和理解了。作为一个记录吧，希望以后自己再看起来方便回顾。