poj2451——半平面交求核面积(O(nlogn))
Prince Remmarguts solved the CHESS puzzle successfully. As an award, Uyuw planned to hold a concert in a huge piazza named after its great designer Ihsnayish.
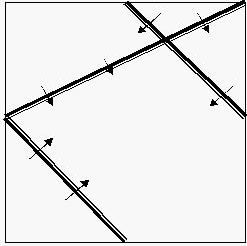
The piazza in UDF - United Delta of Freedom’s downtown was a square of [0, 10000] * [0, 10000]. Some basket chairs had been standing there for years, but in a terrible mess. Look at the following graph.
In this case we have three chairs, and the audiences face the direction as what arrows have pointed out. The chairs were old-aged and too heavy to be moved. Princess Remmarguts told the piazza's current owner Mr. UW, to build a large stage inside it. The stage must be as large as possible, but he should also make sure the audience in every position of every chair would be able to see the stage without turning aside (that means the stage is in the forward direction of their own).
To make it simple, the stage could be set highly enough to make sure even thousands of chairs were in front of you, as long as you were facing the stage, you would be able to see the singer / pianist – Uyuw.
Being a mad idolater, can you tell them the maximal size of the stage?
Input
In the first line, there's a single non-negative integer N (N <= 20000), denoting the number of basket chairs. Each of the following lines contains four floating numbers x1, y1, x2, y2, which means there’s a basket chair on the line segment of (x1, y1) – (x2, y2), and facing to its LEFT (That a point (x, y) is at the LEFT side of this segment means that (x – x1) * (y – y2) – (x – x2) * (y – y1) >= 0).
Output
Output a single floating number, rounded to 1 digit after the decimal point. This is the maximal area of the stage.
Sample Input
3 10000 10000 0 5000 10000 5000 5000 10000 0 5000 5000 0
Hint
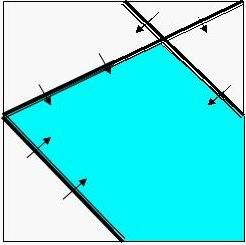
Sample input is the same as the graph above, while the correct solution for it is as below:
I suggest that you use Extended in pascal and long double in C / C++ to avoid precision error. But the standard program only uses double.
题目翻译:
雷马古茨王子成功地解决了CHESS谜题。作为奖项,Uyuw计划在一个巨大的广场上举办一场音乐会,以伟大的设计师伊赫斯纳伊什的名字命名。
UDF - 自由联合三角洲市中心的广场是一个正方形[0,10000] [0,10000]。
一些篮子椅子已经站在那里好几年了,但一团糟。查看下图。
在这种情况下,我们有三把椅子,观众面对的方向,箭头已经指出。椅子老旧,太重了,不能移动。雷马古茨公主告诉广场现任主人UW先生,在广场内建一个大舞台。舞台必须尽可能大,但他还应确保每把椅子每个位置的观众都能看到舞台而不转过身(这意味着舞台是朝着自己的方向前进的)。
简单来说,舞台可以设置得足够高,以确保甚至成千上万的椅子摆在你面前,只要你面对舞台,你将能够看到歌手/钢琴家 - Uyuw。
作为一个疯狂的伊多拉,你能告诉他们舞台的最大大小
吗?
输入
在第一行中,有一个非负整数 N (N <= 20000),表示篮子椅子的数量。以下每行包含四个浮动数字 x1、y1、x2、y2,这意味着在 (x1, y1) 的线段上有一个篮子椅 = (x2, y2), 并面向其 LEFT(该点 (x, y) 位于此段的左侧表示 (x = x1) = (y = y2) (x = x2) * (y = y1) >= 0。
输出
输出单个浮动数字,在小数点后四舍五入为 1 位。这是舞台的最大区域。
这个题本来以为很难的一道题,也是zzy专门为它的O(nlogn)的做法写的题,本来数据很强的,但是poj不给力,把数据改了,然后就是一个傻逼题了,听说O(n^2)也能过,而且不卡double(本来是会卡double的!!QAQ!) 。
题目理解了就知道让你求半平面交后的凸多边形的有向面积,直接叉乘就可以求出来。
读入线段时可以用两点式或者直接求方向向量,注意初始情况有四个线段。
#include
#include
#include
#include
using namespace std;
const double eps = 1e-6;
const int inf=0x3f3f3f3f;
struct Point{
double x, y;
Point(double x = 0, double y = 0):x(x),y(y){}
}p[1005],poly[1005];
int n;
typedef Point Vector;
Vector operator + (Vector A, Vector B){
return Vector(A.x+B.x, A.y+B.y);
}
Vector operator - (Point A, Point B){
return Vector(A.x-B.x, A.y-B.y);
}
Vector operator * (Vector A, double p){
return Vector(A.x*p, A.y*p);
}
int sgn(double x){
if(fabs(x) < eps)
return 0;
if(x < 0)
return -1;
return 1;
}
double Dot(Vector A, Vector B){
return A.x*B.x + A.y*B.y;
}
double Cross(Vector A, Vector B){
return A.x*B.y-A.y*B.x;
}
double Length(Vector A){
return sqrt(Dot(A, A));
}
Vector Normal(Vector A){//向量A左转90°的单位法向量
double L = Length(A);
return Vector(-A.y/L, A.x/L);
}
struct Line{
Point p,p2;//直线上任意一点
Vector v;//方向向量,它的左边就是对应的半平面
double ang;//极角,即从x轴正半轴旋转到向量v所需要的角(弧度)
Line(){}
Line(Point p, Vector v) : p(p), v(v){
ang = atan2(v.y, v.x);
}
void twoPointIntial(Point p,Point p2){
this->p=p;
this->p2=p2;
v=p2-p;
ang=atan2(v.y,v.x);
}
bool operator < (const Line& L) const {//排序用的比较运算符
return ang < L.ang;
}
}l[20005];
//点p在有向直线L的左侧
bool OnLeft(Line L, Point p){
return Cross(L.v, p - L.p) > 0;
}
//两直线交点。假定交点唯一存在
Point GetIntersection(Line a, Line b){
Vector u = a.p - b.p;
double t = Cross(b.v, u)/Cross(a.v, b.v);
return a.p + a.v*t;
}
//半平面交的主过程
int HalfplaneIntersection(Line* L, int n, Point* poly){
sort(L, L + n);//按照极角排序
int fst = 0, lst = 0;//双端队列的第一个元素和最后一个元素
Point *P = new Point[n];//p[i] 为 q[i]与q[i + 1]的交点
Line *q = new Line[n];//双端队列
q[fst = lst = 0] = L[0];//初始化为只有一个半平面L[0]
for(int i = 1; i < n; ++i){
while(fst < lst && !OnLeft(L[i], P[lst - 1])) --lst;
while(fst < lst && !OnLeft(L[i], P[fst])) ++fst;
q[++lst] = L[i];
if(sgn(Cross(q[lst].v, q[lst - 1].v)) == 0){
//两向量平行且同向,取内侧一个
--lst;
if(OnLeft(q[lst], L[i].p)) q[lst] = L[i];
}
if(fst < lst)
P[lst - 1] = GetIntersection(q[lst - 1], q[lst]);
}
while(fst < lst && !OnLeft(q[fst], P[lst - 1])) --lst;
//删除无用平面
if(lst - fst <= 1) return 0;//空集
P[lst] = GetIntersection(q[lst], q[fst]);//计算首尾两个半平面的交点
//从deque复制到输出中
int m = 0;
for(int i = fst; i <= lst; ++i) poly[m++] = P[i];
return m;
}
int main(){
while(scanf("%d",&n)==1){
for(int i=0;i