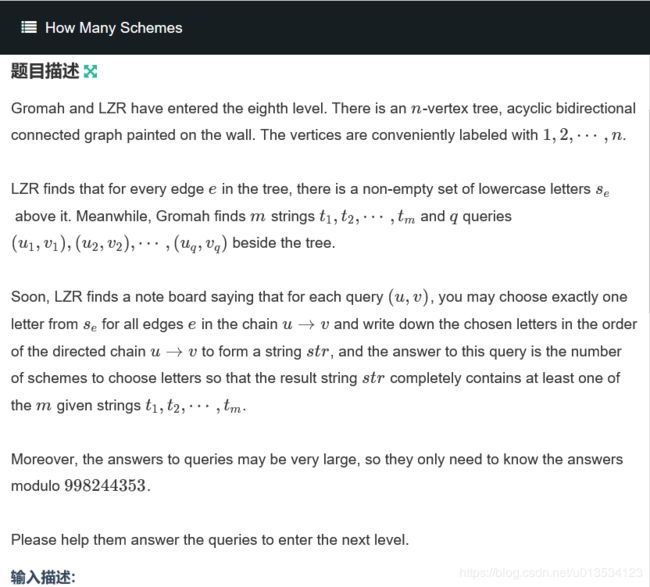
2019牛客多校赛 第八场 H How Many Schemes(AC自动机 + 矩阵 + 向量 + 树链剖分 + 线段树)
大致题意:给你一棵树,每条边上有一个字符串,然后有一些模式串。现在给你一个询问
看起来很难的样子,写起来其实很复杂,但是理解清楚了其实思路也不太难。
首先,既然涉及到匹配问题,而且是多个模式串,很容易想到对模式串建立AC自动机。然后这题模式串长度和不超过40,也很容易可以想到可以和矩阵相关。进而,树上每一条边我都可以建立一个转移矩阵,如果某个位置(x,y)为1,说明经过这条边可以从自动机上的第y个点转移到第x个点且方案数为1。如此,对于一个u到v的路径,我们就把用路上所有的边对应的矩阵左乘到一起,再把结果矩阵乘以初始向量(初始向量0处为1),就可以知道到达所有自动机上的点的方案数。
不过,光知道方案数还是不能知道知道包含至少一个模式串的方案数,所以我们不妨考虑计算未经过一个模式串点的方案数,然后用总方案数减去这个方案。未经过的点的话,我们可以在转移矩阵中,强行把所有的能够到达模式串点的位置都变为0,这样只要任何时刻经过了模式串点,它都不会计算到答案里面。而总方案数,直接是路径上所有字符串的长度的乘积。
如此,我们只需要快速计算两点路径上边对应矩阵的左右乘积和字符串长度乘积。这个我们可以直接上树链剖分和线段树去做,然而我们来分析一下复杂度。询问部分,树链剖分+线段树本身是O(QlogNlogN)的复杂度,加上中间的矩阵乘法就是O(T^3*QlogNlogN)复杂度上确实是会超的好像不是一点点。
由于这题并没有修改,所以我们考虑先对树链剖分+线段树的组合进行优化。考虑树链剖分的原理,当u和v不在同一条链的时候,是直接让深度小的点走到完它所在的链并且计算这一段的贡献。所以我们不妨提前预处理每个点到它链头的矩阵的左右乘积,这样我们在计算某一个点到它链头的贡献的时候就可以直接O(1)计算。当u和v在同一个链的时候,就得用上线段树了,但只有这一次用了线段树。复杂度就是O(T^3*QlogN+QlogN+T^3*N),T^3*N是预处理矩阵左右乘积的复杂度。
然后你会发现这样子好像还是会超那么一点,在那个用线段树那一次统计上。于是考虑利用一下向量的性质。我们本质上是想让路径上所有的矩阵乘在一起,然后最后乘以我们的向量。我们知道这个矩阵运算是具有结合律的,一堆矩阵按顺序乘在一起的结果乘以一个向量,等价于政协矩阵按顺序一个个乘以这个向量。这样做的好处就是,向量左乘一个矩阵,它的复杂度是平方级别的,而不是三次方。于是,我们重写一下线段树,把原本多个区间的矩阵相乘合并,变为直接让矩阵乘以这个向量。如此,最后的复杂度就变成了O(T^2*QlogN+QlogN+T^3*N),恰好可以满足条件。
然后这题的话,还是有很多细节,比如说左乘右乘和根节点矩阵的构造等,自己在好好体会一下。这应该是目前为止手写的代码最长的一道题了。具体见代码:
#include
#define INF 0x3f3f3f3f3f3f3f3fll
#define eps 1e-4
#define pi 3.141592653589793
#define P 1000000007
#define LL long long
#define pb push_back
#define fi first
#define se second
#define cl clear
#define si size
#define lb lower_bound
#define ub upper_bound
#define bug(x) cerr<<#x<<" : "< g[N];
int num,n,m,q,t[N],tot;
char ss[100];
struct Matrix
{
int a[M][M];
Matrix(){memset(this,0,sizeof(Matrix));}
Matrix operator *(const Matrix x) const
{
Matrix ans;
for(int i=0;i q;
q.push(root);
while(!q.empty())
{
int o=q.front();
T[o].cnt=T[o].cnt|T[T[o].fail].cnt;
for(int i=0;i<26;i++)
{
if (!T[o].ch[i])
{
T[o].ch[i]=T[T[o].fail].ch[i];
continue;
}
if (o!=root)
{
int fa=T[o].fail;
while(fa&&!T[fa].ch[i]) fa=T[fa].fail;
T[T[o].ch[i]].fail=T[fa].ch[i];
} else T[T[o].ch[i]].fail=root;
q.push(T[o].ch[i]);
} q.pop();
}
}
inline void build(int l,char *s)
{
memset(a[l].a,0,sizeof(a[l].a));
for(int i=0;i>1;
build(ls,l,mid);
build(rs,mid+1,r);
push_up(i);
}
void getlsum(int i,int l,int r,Vector &ans)
{
if (T[i].l==l&&T[i].r==r) {ans.LeftMulti(T[i].lsum);return;}
int mid=(T[i].l+T[i].r)>>1;
if (mid>=r) getlsum(ls,l,r,ans);
else if (mid>1;
if (mid>=r) getrsum(ls,l,r,ans);
else if (mid>1;
if (mid>=r) return getnum(ls,l,r);
else if (midsize[son[u]]) son[u]=y;
}
}
void dfs2(int u,int f)
{
top[u]=f; id[u]=++num;
if (son[u]) dfs2(son[u],f);
for(int i=0;i stk;
while (tp1 != tp2)
if (dep[tp1] > dep[tp2])
{
ans.LeftMulti(suf[id[u]]);
cnt=(LL)cnt*t[id[u]]%mod;
u=fa[tp1]; tp1=top[u];
} else
{
stk.push(id[v]);
v=fa[tp2]; tp2=top[v];
}
if (dep[u] < dep[v])
{
seg.getlsum(1,id[u]+1,id[v],ans);
cnt=(LL)cnt*seg.getnum(1,id[u]+1,id[v])%mod;
} else
if (dep[u] > dep[v])
{
seg.getrsum(1,id[v]+1,id[u],ans);
cnt=(LL)cnt*seg.getnum(1,id[v]+1,id[u])%mod;
}
while(!stk.empty())
{
ans.LeftMulti(pre[stk.top()]);
cnt=(LL)cnt*t[stk.top()]%mod; stk.pop();
}
for(int i=0;iread
bool IOerror=0;
inline char nc(){
static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE;
if (p1==pend){
p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin);
if (pend==p1){IOerror=1;return -1;}
}
return *p1++;
}
inline bool blank(char ch){return ch==' '||ch=='\n'||ch=='\r'||ch=='\t';}
inline void read(int &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (sign)x=-x;
}
inline void read(char *s){
char ch=nc();
for (;blank(ch);ch=nc());
if (IOerror)return;
for (;!blank(ch)&&!IOerror;ch=nc())*s++=ch;
*s=0;
}
}
struct Ostream_fwrite{
char *buf,*p1,*pend;
Ostream_fwrite(){buf=new char[BUF_SIZE];p1=buf;pend=buf+BUF_SIZE;}
void out(char ch){
if (p1==pend){
fwrite(buf,1,BUF_SIZE,stdout);p1=buf;
}
*p1++=ch;
}
void print(int x){
static char s[15],*s1;s1=s;
if (!x)*s1++='0';if (x<0)out('-'),x=-x;
while(x)*s1++=x%10+'0',x/=10;
while(s1--!=s)out(*s1);
}
void print(char *s){while (*s)out(*s++);}
void flush(){if (p1!=buf){fwrite(buf,1,p1-buf,stdout);p1=buf;}}
~Ostream_fwrite(){flush();}
}Ostream;
inline void print(int x){Ostream.print(x);}
inline void print(char *s){Ostream.print(s);}
inline void flush(){Ostream.flush();
}
using namespace IO;
int main(){
read(n);
read(m);
read(q);
Edge tmp;
for(int i=1;i