使用Jerasure library实现一些erasure coding

该库source code及其说明文档所在：http://web.eecs.utk.edu/~plank/plank/papers/CS-08-627.html

Github上也贴出了代码：https://github.com/tsuraan/Jerasure

如果我们直接google的话可以搜到两篇相关的博文，在此也贴出来，供大家深入学习：

1，http://www.cnblogs.com/yuki-lau/p/3365878.html

2，http://blog.chinaunix.net/uid-20196318-id-3277600.html

《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》《》

该库使用的编程语言为Unix下的C/C++。

所给的technique report即时一个简要的使用手册也是一个对于内部实现的介绍说明。

一，介绍

In this library, it seems that the raw encoding methods can not guarantee any level of security of the input files , because there are all  systematic codes, whose  raw file blocks are  still  "among" the encoded blocks. This is illustrated in the introduction part of this technique report.

 

“Most codes have a third parameter w, which is theword size. The description of a code views each device as
having w bits worth of data. ”说白了，就是指定最基本的编码操作单位，把多少个bits作为一个基本元素。（Wrong！）。

根据这篇文档的意思，word size是最高层的对于device的一种划分，形成一个个packet，而每一个packet都是同样的实际大小，这个大小称为packet size，所以总的device的大小就是w*（packet size）

这个库的结构还是比较清晰的：“This library is broken into five modules, each with its own header file and implementation in C. Typically, when using a code, one only needs three of these modules: galois, jerasure and one of the others.”

五部分满足较好的模块独立性：

有一些参数的意义必须要明白才能较好的使用库的接口：

二，示例examples

最主要的还是要借鉴Examples文件夹下实现的一些反映其内部各函数调用方法的程序：

其中，我们尤其关注Reed-Solomon的各种相关encoder/decoder：

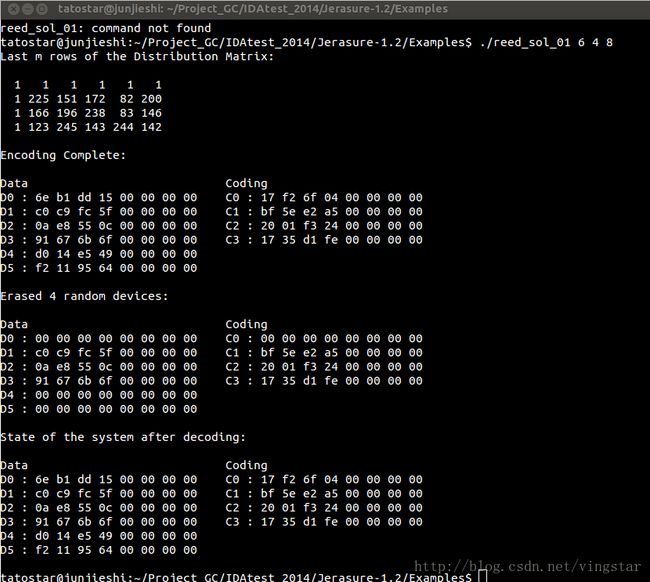
1，Classic Reed-Solomon Coding:

一般的输入参数为k,m,w三个，而在其optimization for RAID-6中，m is equal to two,不需要这一参数。

"reed sol 01.c: This takes three parameters: k, m and w. It performs a classic Reed-Solomon w coding of k devices onto m devices, using a Vandermonde-based distribution matrix in GF (2 ). w must be 8, 16 or 32. Each device is set up to hold sizeof(long) bytes. It uses reed sol vandermonde coding matrix() to generate the distribution matrix, and then procedures from jerasure.c to perform the coding and decoding."

 in its corresponding example program, the raw input data is randomly generated and some of them are also erased randomly:

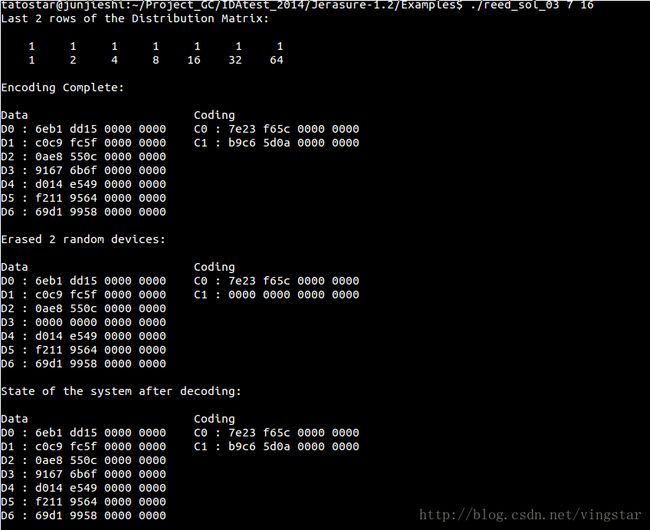
"reed sol 03.c: This takes w two parameters: k and w. It performs RAID-6 coding using Anvin’s optimization [Anv07] in GF (2 ), where w must be 8, 16 or 32. It then decodes using jerasure matrix decode()."

2, Cauchy Reed-Solomon Coding

It is different with the classic one in the inner implementation of the matrix.

 cauchy 02.c: This takes three parameters: k, m and w. (In this and the following examples, packetsize is sizeof(long).) It calls cauchy original coding matrix() to create an Cauchy matrix, converts it to a bit-matrix then encodes and decodes with it. Smart scheduling is employed. Lastly, it uses cauchy xy coding matrix() to create the same Cauchy matrix. It verifies that the two matrices are indeed identical.

tatostar@junjieshi:~/Project_GC/IDAtest_2014/Jerasure-1.2/Examples$ ./cauchy_02 2 2 8
Matrix has 114 ones


142 244
244 142


Smart Encoding Complete: - 448 XOR'd bytes


Data                          Coding
D0  p0 : 15ddb16e 5ffcc9c000000000    C0  p0 : 39655ddc 204e8bcc00000000
    p1 : 5ffcc9c0 c55e80a00000000        p1 : 204e8bcc 732d8eb900000000
    p2 : 0c55e80a 6f6b679100000000        p2 : 732d8eb9 71a0886500000000
    p3 : 6f6b6791 49e514d000000000        p3 : 71a08865 1d8b8a8400000000
    p4 : 49e514d0 649511f200000000        p4 : 1d8b8a84 c9be4300000000
    p5 : 649511f2 5899d16900000000        p5 : 00c9be43 451be36e00000000
    p6 : 5899d169 2f33bbae00000000        p6 : 451be36e 1c9833c800000000
    p7 : 2f33bbae 00000000        p7 : 1c9833c8 00000000
D1  p0 : 6fdc16ba 5f5f46b400000000    C1  p0 : 39476f0a 6f20fe8c00000000
    p1 : 5f5f46b4 3918084800000000        p1 : 6f20fe8c 4ee712500000000
    p2 : 39180848 2d46f73b00000000        p2 : 04ee7125 68c54d5400000000
    p3 : 2d46f73b 5dc3340b00000000        p3 : 68c54d54 41b417b900000000
    p4 : 5dc3340b 214ef45c00000000        p4 : 41b417b9 3617c5fd00000000
    p5 : 214ef45c 327837ea00000000        p5 : 3617c5fd 3f9bf91800000000
    p6 : 327837ea 636dda6600000000        p6 : 3f9bf918 1c198e6a00000000
    p7 : 636dda66 00000000        p7 : 1c198e6a 00000000


Erased 2 random devices:


Data                          Coding
D0  p0 : 15ddb16e 5ffcc9c000000000    C0  p0 : 39655ddc 204e8bcc00000000
    p1 : 5ffcc9c0 c55e80a00000000        p1 : 204e8bcc 732d8eb900000000
    p2 : 0c55e80a 6f6b679100000000        p2 : 732d8eb9 71a0886500000000
    p3 : 6f6b6791 49e514d000000000        p3 : 71a08865 1d8b8a8400000000
    p4 : 49e514d0 649511f200000000        p4 : 1d8b8a84 c9be4300000000
    p5 : 649511f2 5899d16900000000        p5 : 00c9be43 451be36e00000000
    p6 : 5899d169 2f33bbae00000000        p6 : 451be36e 1c9833c800000000
    p7 : 2f33bbae 00000000        p7 : 1c9833c8 00000000
D1  p0 : 00000000 00000000    C1  p0 : 00000000 00000000
    p1 : 00000000 00000000        p1 : 00000000 00000000
    p2 : 00000000 00000000        p2 : 00000000 00000000
    p3 : 00000000 00000000        p3 : 00000000 00000000
    p4 : 00000000 00000000        p4 : 00000000 00000000
    p5 : 00000000 00000000        p5 : 00000000 00000000
    p6 : 00000000 00000000        p6 : 00000000 00000000
    p7 : 00000000 00000000        p7 : 00000000 00000000


State of the system after decoding: 464 XOR'd bytes


Data                          Coding
D0  p0 : 15ddb16e 5ffcc9c000000000    C0  p0 : 39655ddc 204e8bcc00000000
    p1 : 5ffcc9c0 c55e80a00000000        p1 : 204e8bcc 732d8eb900000000
    p2 : 0c55e80a 6f6b679100000000        p2 : 732d8eb9 71a0886500000000
    p3 : 6f6b6791 49e514d000000000        p3 : 71a08865 1d8b8a8400000000
    p4 : 49e514d0 649511f200000000        p4 : 1d8b8a84 c9be4300000000
    p5 : 649511f2 5899d16900000000        p5 : 00c9be43 451be36e00000000
    p6 : 5899d169 2f33bbae00000000        p6 : 451be36e 1c9833c800000000
    p7 : 2f33bbae 00000000        p7 : 1c9833c8 00000000
D1  p0 : 6fdc16ba 5f5f46b400000000    C1  p0 : 39476f0a 6f20fe8c00000000
    p1 : 5f5f46b4 3918084800000000        p1 : 6f20fe8c 4ee712500000000
    p2 : 39180848 2d46f73b00000000        p2 : 04ee7125 68c54d5400000000
    p3 : 2d46f73b 5dc3340b00000000        p3 : 68c54d54 41b417b900000000
    p4 : 5dc3340b 214ef45c00000000        p4 : 41b417b9 3617c5fd00000000
    p5 : 214ef45c 327837ea00000000        p5 : 3617c5fd 3f9bf91800000000
    p6 : 327837ea 636dda6600000000        p6 : 3f9bf918 1c198e6a00000000
    p7 : 636dda66 00000000        p7 : 1c198e6a 00000000


Generated the identical matrix using cauchy_xy_coding_matrix()

cauchy 03.c: This is identical to cauchy 02.c, except that it improves the matrix with cauchy_improve_coding_matrix().

 cauchy 04.c: Finally, this is identical to the previous two, except it calls cauchy good general coding matrix(). Note, when m = 2, w <=11 and k <=1023, these are optimal Cauchy encoding matrices. That’s not to say that they are optimal RAID-6 matrices (RDP encoding [CEG 04], and Liberation encoding [Pla08b] achieve this), but they are the best Cauchy matrices.

3, Encoder / Decoder 

这里主要是介绍如何将上述的各种coding直接用来处理文件。这对于我们来说是非常有利的。

 encoder.c: This program is used to encode a file using any of the available methods in jerasure. It takes seven
parameters:
– inputfile or negative number S: either the file to be encoded or a negative number S indicating that a
random file of size −S should be used rather than an existing file
– k: number of data files
– m: number of coding files
– coding technique: must be one of the following:
             ∗ reed sol van: calls reed sol vandermonde coding matrix() and jerasure matrix encode()
             ∗ reed sol r6 op: calls reed sol r6 encode()

             ∗ cauchy orig: calls cauchy original coding matrix(), jerasure matrix to bitmatrix, jerasure smart bitmatrix to schedule, and jerasure-schedule encode()
             ∗ cauchy good: calls cauchy good general coding matrix(), jerasure matrix to bitmatrix, jerasure-smart bitmatrix to schedule, and jerasure schedule encode()
             ∗ liberation: calls liberation coding bitmatrix, jerasure smart bitmatrix to schedule, and jerasure-schedule encode()
             ∗ blaum roth: calls blaum roth coding bitmatrix, jerasure smart bitmatrix to schedule, and jerasure-schedule encode()
             ∗ liber8tion: calls liber8tion coding bitmatrix, jerasure smart bitmatrix to schedule, and jerasure-schedule encode()

– w: word size
– packetsize: can be set to 0 if not required by the selected coding method
– buffersize: approximate size of data (in bytes) to be read in at a time; will be adjusted to obtain a proper
multiple and can be set to 0 if desired

This program reads in inputfile (or creates random data), breaks the file into k blocks, and encodes the file into m blocks. It also creates a metadata file to be used for decoding purposes. It writes all of these into a directory named Coding. The output of this program is the rate at which the above functions run and the total rate of running of the program, both given in MB/sec.

In reality, we found that the input file should have a suffix name, such as using Cfile.cc rather than Cfile.

 decoder.c: This program is used in conjunction with encoder to decode any files remaining after erasures and reconstruct the original file.The only parameter for decoder is inputfile, the original file that was encoded.This file does not have to exist; the file name is needed only to find files created by encoder, which should be in the Coding directory. After some number of erasures, the program locates the surviving files from encoder and recreates the original file if at least k of the files still exist. The rate of decoding and the total rate of running the program are given as output.

ATTENTION: When using these routines, one should pay attention to packet and buffer sizes.