leetcode刷题(中序遍历与前序或后序遍历构建二叉树)
题目一描述:
根据一棵树的中序遍历与后序遍历构造二叉树。
题目一分析:
1.后续遍历:先遍历一颗树的左结点在遍历一棵树的右结点最后是根节点
2.中序遍历:先遍历一棵树的左结点再遍历一颗树的根节点最后遍历一棵树的右结点
后续遍历中的最后一个节点是树的根节点,对应于中序遍历中的一个元素该元素的左边位置为左子树,该节点的右边的元素为根节点的右子树。
举个栗子:
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
代码如下:
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
//将当前中序遍历的位置记录先来,后续遍历最后一个元素找自己的左孩子和自己的右孩子比较方便
Map<Integer,Integer> map = new HashMap<>();
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return buildTree(postorder,0,postorder.length-1,map,0,inorder.length-1);
}
//重载方法,传入后续遍历的数组,当前数组的左指针,当前数组的右指针,传入记录根位置的map集合,以及中序遍历的左位置和右位置
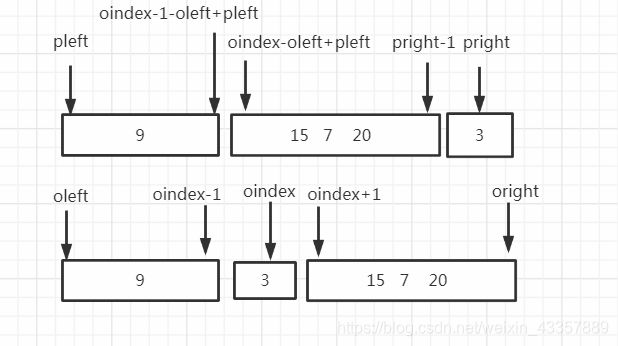
public TreeNode buildTree(int[] postorder,int pleft,int pright, Map<Integer,Integer> map,int oleft,int oright) {
if(oleft>oright||pleft>pright)return null;
//后续遍历最右端的结点是根节点
TreeNode root = new TreeNode(postorder[pright]);
//获取根节点在中序遍历中的位置
int oindex = map.get(postorder[pright]);
//根据中序遍历递归传入左子树和右子树迭代
root.left = buildTree(postorder,pleft,oindex-1-oleft+pleft,map,oleft,oindex-1);
root.right = buildTree(postorder,oindex-oleft+pleft,pright-1,map,oindex+1,oright);
return root;
}
}
题目二描述:
根据一棵树的中序遍历与前序遍历构造二叉树。
题目二分析:
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
原理同上
代码如下:
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder==null||inorder==null){
return null;
}
Map<Integer,Integer> map = new HashMap<>();
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return buildTree(preorder,0,preorder.length-1,map,0,inorder.length-1);
}
public TreeNode buildTree(int[] preorder, int pleft,int pright,Map<Integer,Integer> map,int oleft,int oright) {
if(pleft>pright||oleft>oright){
return null;
}
int tmp = preorder[pleft];
TreeNode root = new TreeNode(tmp);
int oindex = map.get(preorder[pleft]);
//x-(pleft+1) = oindex-1-oleft,x= oindex -oleft+pleft
root.left=buildTree(preorder,pleft+1,oindex - oleft+pleft,map,oleft,oindex-1);
root.right = buildTree(preorder,oindex - oleft+pleft+1,pright,map,oindex+1,oright);
return root;
}
}
小结:使用中序遍历和前序或者后序遍历能够构建出一颗二叉树,但是对于前序遍历和后续遍历无法构建二叉树。
回顾前序遍历、后续遍历、中序遍历的知识点:
// 前序遍历二叉树,中左右
public static void preorder(TreeNode root) {
if (root == null)
return;
System.out.print(root.val + " ");
if (root.left != null)
preorder(root.left);
if (root.right != null)
preorder(root.right);
}
// 中序遍历二叉树,左中右
public static void inorder(TreeNode root) {
if (root == null)
return;
if (root.left != null)
inorder(root.left);
System.out.print(root.val + " ");
if (root.right != null)
inorder(root.right);
}
// 后序遍历二叉树左右中
public static void postorder(TreeNode root) {
if (root == null)
return;
if (root.left != null)
postorder(root.left);
if (root.right != null)
postorder(root.right);
System.out.print(root.val + " ");
}