【2019年沈阳网络赛D题】【Fish eating fruit】【树形dp(转移写法)】

题目链接：
https://nanti.jisuanke.com/t/41403
题意：
题目给了一个$N$个点$N-1$条边的树形图
现在每次出行的交通工具是鱼，而鱼对于路径长度有不同的喜好
如果总路径长度是3的倍数，那么鱼需要路径长度数量的 榴莲
如果总路径长度%3=1，那么鱼需要路径长度数量的 木瓜
如果总路径长度%3=2，那么鱼需要路径长度数量的 牛奶果
现在问，从图上的每个点$i$到达除了$i$之外的所有点（$N\ast (N-1)$条路径），总共需要花费多少榴莲、木瓜、牛奶果
题解：
这里暴力解法是以每个点为根节点，然后算答案，复杂度为$O(n^2)$，显然会T
那么考虑根节点的转移，也就是以点$1$为根节点，然后从点$1$开始转移树根(转移树根复杂度不能太高，要那种快速计算的才行)，计算答案，复杂度为$O(n)$
如果没有见过这种类型的题目，可以看下洛谷P2986(这题会比较简单)

这里只需要两次$dfs$即可完成计算：
第一次$dfs$计算以点$u$为根节点所得到的花费
第二次$dfs$计算从$u$转移到其他点作为根时得到的花费，只要不断地转移，直到遍历所有点（即所有点都做了一次树根），即可得到答案

这里我记$dis[i]$为点$i$的子节点到达点$i$的路径之和
显然，若记子节点到达点$i$的长度为$d$，那么这样的路径可以分成三种
①$d\%3=0$
②$d\%3=1$
③$d\%3=2$
不妨分别记做$dis[i][0],dis[i][1],dis[i][2]$
然后我们再记录路径的数量$num[i][0],num[i][1],num[i][2]$
记当前点为$u$，子节点为$son$，他们之间的路径长度为$w$，那么我们就有了状态转移方程

num[son][0]++;
for (int j = 0; j <= 2; j++) {
		dis[u][(w + j) % 3] += num[son][j] * w + dis[son][j];
		num[u][(w + j) % 3] += num[son][j];
	}

举一个简单的例子，如果原来这条路属于③，再加上一条长度为$2$的路，那么这条路将会划分到分类②当中，因为$(2+2)\%3=1$
而为什么这里$num[son][0]$需要加一呢？因为原来的$num[son][j]$里面并不包含子节点$son$到点$i$的路，所以这里加上去
搞懂这个之后，我们的第一个dfs就能很轻松的写出来了

void dfs1(int u, int fa, int d) {
	dis[u][0] = dis[u][1] = dis[u][2] = 0;
	num[u][0] = num[u][1] = num[u][2] = 0;
	for (int i = head[u]; i; i = e[i].nxt)
		if (e[i].to != fa) {
			int son = e[i].to; ll w = e[i].w;
			dfs1(son, u, d + w);
			num[son][0]++;
			for (int j = 0; j <= 2; j++) {
				dis[u][(w + j) % 3] += num[son][j] * w + dis[son][j];
				num[u][(w + j) % 3] += num[son][j];
			}
		}
}

然后就是第二个dfs
本来我们是以点$i$为根，那么如何快速计算以$i$的子节点$son$为根的答案呢？

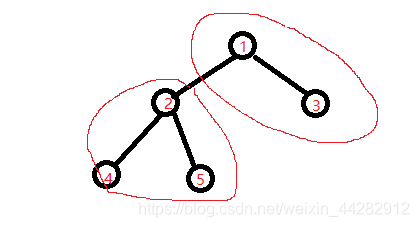
假如我们这里将树根从点1转移到点2，那么其实，只是点$1,3$多走了一段路1->2，点$2,4,5$少走了一段路，然后考虑一下转移即可

void dfs2(int u, int fa) {
	for (int i = head[u]; i; i = e[i].nxt)
		if (e[i].to != fa) {
			int son = e[i].to; ll w = e[i].w;
			//记录下原来的dis,num  后面需要还原
			ll d1[10], d2[10], n1[10], n2[10];
			for (int j = 0; j <= 2; j++)d1[j] = dis[u][j], d2[j] = dis[son][j], n1[j] = num[u][j], n2[j] = num[son][j];

			//因为现在树根是son，原来的树根u变为son的子节点
			//所以原来的树根u的路径数量要减去son的路径数量(也就是dfs1里面倒过来处理一遍)
			for (int j = 0; j <= 2; j++) {
				dis[u][(w + j) % 3] -= num[son][j] * w + dis[son][j];
				num[u][(w + j) % 3] -= num[son][j];
			}
			num[son][0]--;

			//同dfs1里面，就是父子交换
			num[u][0]++;
			for (int j = 0; j <= 2; j++) {
				dis[son][(w + j) % 3] += num[u][j] * w + dis[u][j];
				num[son][(w + j) % 3] += num[u][j];
			}

			fuck(son);//统计答案
			dfs2(son, u);//递归遍历

			//还原
			for (int j = 0; j <= 2; j++)dis[u][j] = d1[j], dis[son][j] = d2[j], num[u][j] = n1[j], num[son][j] = n2[j];

		}
}

最后上总代码:

#include<bits/stdc++.h>
#define INF	0x3f3f3f3f
#define sz	sizeof
using namespace std;
typedef long long			ll;
typedef unsigned long long	ull;
typedef pair<int, int>		pii;
const int MAX = 1e4 + 10;
const int mod = 1e9 + 7;

struct edge {
	int nxt, to;
	ll w;
}e[MAX << 1];

int tot, head[MAX];

void add(int u, int v, ll w) {
	e[++tot].nxt = head[u];
	e[tot].to = v;
	e[tot].w = w;
	head[u] = tot;
}

int N;
ll ans[10], dis[MAX][3], num[MAX][3];

void fuck(int u) {//统计答案
	for (int i = 0; i <= 2; i++)
		(ans[i] += dis[u][i]) %= mod;
}

void dfs1(int u, int fa, int d) {
	dis[u][0] = dis[u][1] = dis[u][2] = 0;
	num[u][0] = num[u][1] = num[u][2] = 0;
	for (int i = head[u]; i; i = e[i].nxt)
		if (e[i].to != fa) {
			int son = e[i].to; ll w = e[i].w;
			
			dfs1(son, u, d + w);
			
			num[son][0]++;
			for (int j = 0; j <= 2; j++) {
				dis[u][(w + j) % 3] += num[son][j] * w + dis[son][j];
				num[u][(w + j) % 3] += num[son][j];
			}
		}
}

void dfs2(int u, int fa) {
	for (int i = head[u]; i; i = e[i].nxt)
		if (e[i].to != fa) {
			int son = e[i].to; ll w = e[i].w;
			//记录下原来的dis,num  后面需要还原
			ll d1[10], d2[10], n1[10], n2[10];
			for (int j = 0; j <= 2; j++)d1[j] = dis[u][j], d2[j] = dis[son][j], n1[j] = num[u][j], n2[j] = num[son][j];

			//因为现在树根是son，原来的树根u变为son的子节点
			//所以原来的树根u的路径数量要减去son的路径数量(也就是dfs1里面倒过来处理一遍)
			for (int j = 0; j <= 2; j++) {
				dis[u][(w + j) % 3] -= num[son][j] * w + dis[son][j];
				num[u][(w + j) % 3] -= num[son][j];
			}
			num[son][0]--;

			//同dfs1里面，就是父子交换
			num[u][0]++;
			for (int j = 0; j <= 2; j++) {
				dis[son][(w + j) % 3] += num[u][j] * w + dis[u][j];
				num[son][(w + j) % 3] += num[u][j];
			}

			fuck(son);//统计答案
			dfs2(son, u);//递归遍历

			//还原
			for (int j = 0; j <= 2; j++)dis[u][j] = d1[j], dis[son][j] = d2[j], num[u][j] = n1[j], num[son][j] = n2[j];

		}
}


int main() {
	while (~scanf("%d", &N)) {
		tot = 0;
		memset(ans, 0, sz(ans));
		memset(head, 0, sz(head));
		for (int i = 1; i < N; i++) {
			int u, v; ll w;
			scanf("%d%d%lld", &u, &v, &w);
			u++, v++;
			add(u, v, w); add(v, u, w);
		}
		dfs1(1, 0, 0);//随便找一个点为树根
		fuck(1);//统计答案
		dfs2(1, 0);//从刚才找的树根开始转移
		printf("%lld %lld %lld\n", ans[0], ans[1], ans[2]);
	}
	return 0;
}