线段树入门（Segment Tree）详细整理（超简单易学的数据结构）

线段树入门（Segment Tree）~详细整理（超简单易学的数据结构）

前言：理解线段树着实花了我很多时间，主要之前一直有个误区，就是对线段树中存储的信息，我认为只能是区间和，可万万没想到呀，它还可以是别的东西：区间最小值、区间最大值等等呀，我​表示(已黑化)，好了，言归正传，博主是完全理解了线段树之后才有勇气写这篇文章的，所以我是根据一个完全初学者到理解线段树的过程来写下这篇文章的，不会像其他文章一下难以理解，当然，本文也只是我学习整理的，如果有错误的话，还请评论区留言或私信我，共同进步。

线段树讲解共有两篇，这一篇为入门，另一篇为进阶。

一、什么是线段树？

• 线段树的基本概念

  在深入学习线段树之前，我们首先要了解线段树是什么？线段树本质也是一颗二叉搜索树，也被认为是区间树（即每个结点都有一段区间，我们也认为是线段）。那有小伙伴可能就要问了，什么是二叉搜索树？二叉搜索树顾名思义：前提是一颗二叉树，它的每个结点度都小于等于2，即每个结点最多有两个子树。其次就是搜索，这是关键，我们这个线段树在其中都有一个区间，那么搜索即是可以在这个区间上搜索你想要的值，这就是搜索，其中，每个结点存储的信息是由你来定的，如果你想求区间和，那么就可以存储区间和，如果你想求区间最大值，那么你可以存储区间最大值，只要可行，你都可以进行你想要的操作。

  ---

• 线段树的注意事项

  1. 在给定了大小给定了叶子结点数目的时候这个线段树就已经确定了，我们不能进行添加和删除元素，不是说不能对已有叶子结点赋值，是不能对其进行扩大或者减小。因为在大多数情况中，对于线段树来说，区间本身都是固定的，不考虑新增和删除元素。所以用数组存储的话，直接用静态数组就好了，不用动态数组。

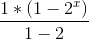  2. 线段树的大小一定要开叶子结点数目（即原有点对点的数据数组大小）的四倍。例如叶子结点数目是maxn，那么我们通常会开线段树的大小为maxn<<2。因为线段树也是一颗完全二叉树，当最大的时候可能是满二叉树。我们来证明一下，我们这样想：最深一层的数目是n，则此线段树的高度为$\lceil$${\log }_{2}n\rceil$,我们可知$\lceil$${\log }_{2}n\rceil$ $\le$ $lo{g}_{2}n+1$。那么我们通过然后通过等比数列求和求得二叉树的节点个数，具体公式为，（x为树的层数，为树的高度+1），化简可得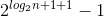,整理之后即为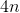（近似计算忽略掉-1）

  3. 我们进行乘除法运算的时候要使用位运算（<< >>一定要仔细理解这两个运算符），而避免使用基本的数学运算，因为我们会频繁使用结点坐标更新，用位运算会更快一点，而且还可以防WR。

  4. 在表示坐标的时候，若一个结点下标为i，那么它的父节点就是i>>1。如果这个结点是这个父节点的左孩子，那么右孩子下标就是i+1。如果这个结点是父节点的右孩子，那么左孩子的下标就是i-1。那个这个结点的左孩子下标就是i<<1，右孩子下标就是(i<<1)=1（这里一定要使用括号改变运算符优先级，因为位运算的优先级属实低。）

  5. 要根据你想解决的问题来设置结点的数据信息。区间求和和区间最值所进行的是不太一样的，所更改的信息也都要注意，但都是一个本质，就是从下往上更新，到达根节点就退出。

  6. 线段树不一定是满二叉树，也就是说线段树的叶子结点不一定是在最后一层。线段树也不一定是完全二叉树（切记！）。但我们可以把线段树看成是满二叉树，对于不存在的结点我们视为空就行。

• 线段树能解决的问题

  线段树的适用范围很广，可以在线维护修改以及查询区间上的最值，求和。使用一维线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。线段树更可以扩充到二维线段树（矩阵树）和三维线段树（空间树），这里我们不作讲解。（其实博主也暂时不会）

你问我线段树算什么东西？今天我就告诉你，单点、区间朴素查询处理做的我线段树能做！单点、区间朴素查询没有的速度我有！这就是线段树。（战术后仰）

二、线段树的基本内容

我们先看一颗线段树：

不然发现线段树的特点，每个结点都有一个值和区间，每个结点的左右孩子都存储了父结点的一半的区间，且它们的序号是按照层次顺序编号的。在日常处理中，我们通常是使用结构体数组来作为线段树的存储结构，因为这样我们就可以利用下标的关系来找到父节点和孩子结点了。例如我们已知一个结点的下标为i，那么：

• 对于父结点：i>>1（这个进行的操作其实就是i/2，前面提到，这样会快很多）

  具体证明也很简单，把线段树看成一个完全二叉树（空结点也当作使用）对于任意一个结点i来说，它所在此二叉树的$lo{g}_{2}i$ 层，则此层共有$2^{log2(i)}$个结点，同样对于k的左子树那层来说有$2^{lo{g}_{2}k+1}$个结点，则结点k和左子树间隔了$2\ast 2^{lo{g}_2(i)}-i+2\ast (i-2^{lo{g}_2(k)})$个结点，然后这就很简单就得到$k+2\ast 2^{lo{g}_2(k)}-k+2\ast (k-2^{log2(k)})=2\ast k$的关系了吧，右子树也就等于左子树结点+1。

• 对于左孩子结点：左孩子下标：i<<1（这些是同理的，即是由父结点推孩子结点。）

• 对于右孩子结点：右孩子下标：i<<1|1

了解了这些关系，我们是有能力去建立一颗线段树的，因为线段树也是树，所以我们自然可以利用递归的思想去建树，不会很难，我也写全了注释。

const int maxn = 1e5;//最大值。
struct Node{
	int left;  //左端点
	int right; //右端点
	int value;//代表区间[left,right]的信息，可以是区间和，也可以是区间最值。
}node[maxn<<2];//这里我们要开4倍大小，防止数据溢出
int father[maxn];//存储原来数据在线段树中的下标，易于从下向上更新区间数据。例如father[i]表示原来的第i个数据在线段树中的下标，这些在线段树中都是叶子结点。
void BuildTree(int i,int l,int r){
	node[i].left=l;node[i].right=r;//存储各自结点的区间
	node[i].value=0;                     //初始化为0.
	if(l==r){                    //说明已经到了叶子结点。
		father[l]=i;//存储下标。
		return;
	}
	BuildTree(i<<1,l,(l+r)/2); //递归初始化左子树
	BuildTree((i<<1)+1,(l+r)/2+1,r);//递归初始化右子树。
}

这样，我们的线段树就建好了。我们来看线段树有哪些基本操作吧。

三、线段树的基本操作

我们这里以结点的值value代表区间和来处理。

1、点更新

这很好办，有没有注意我们是使用了一个father数组，如果我在原数组中修改第i个元素的值，我们是直接可以node[father[i]].value=w，这就是我们使用father数组的好处，那你可能会问了，我们这样是不是要使用三个数组？大可不必，我们没必要给原有数据开一个数组存放，因为我们本身就已经把数据放在线段树中了，不管线段树中存放的是区间和还是区间最值，对于叶子结点来说，它就是本身。那么我们加入了点，自然也要更新整棵树，那有关这个叶子结点到根节点的路径自然全部都是要更新的，我们则是从下往上利用递归思想来更新的。

void UpdateTree(int ri){
	if(ri==1){
		return;
	}
	int fi=ri>>1;//获得父结点下标。
	node[fi].value=node[fi<<1].value+node[fi<<1|1].value;//两段区间总和。
	UpdateTree(fi);
}

2、区间查询

我们有了线段树，可却不对它进行相关查询，那这颗线段树也只是精致的花瓶而已。我们最重要的就是进行区间查询，现在如果我想知道某个区间和的话，我们应该怎样来处理呢？我们知道根节点是存放了整个区间的信息，然后它的孩子结点则存放了它一半区间的信息，这样则显而易见，我们从根节点开始自上往下查询即可。我们本着下面的思想就一目了然了。

1、如果这个区间被完全包括在目标区间里面，直接返回这个区间的值

2、如果这个区间的左儿子和目标区间有交集，那么搜索左儿子

3、如果这个区间的右儿子和目标区间有交集，那么搜索右儿子

OK，整活。

//区间查询，调用函数时为QueryTree(1,l,r)，即从根节点自上往下查询。
int QueryTree(int i,int l,int r){
	int sum=0;
	if(l==node[i].left&&r==node[i].right){
		//如果刚好就是这个区间，我们直接返回。
		sum+=node[i].value;
		return sum;
	}
	i=i<<1;
	if(l<=node[i].right){
		//说明部分包含左子树
		if(r<=node[i].right){
			//说明全包含在左子树。
			sum+=QueryTree(i,l,r);
		}
		else{
			sum+=QueryTree(i,l,node[i].right);
		}
	}
	i+=1;
	if(r>=node[i].left){
		//说明部分包含右子树
		if(l>=node[i].left){
			//说明全包含在右子树。
			sum+=QueryTree(i,l,r);
		}
		else{
			sum+=QueryTree(i,node[i].left,r);
		}
	}
	return sum; //返回求得的区间和。
}

区间查询不断二分，易知时间复杂度为O($lo{g}_{2}n$)。

线段树的基本操作就是这些，当然，这只是入门，灵活使用线段树以及更深层次的利用线段树的道路还很长，我们一起加油！

---

主函数部分测试：

int main(){
	freopen("in.txt", "r", stdin);//提交的时候要注释掉
	ios::sync_with_stdio(false);//打消iostream中输入输出缓存，节省时间。
	cin.tie(0); cout.tie(0);//可以通过tie(0)（0表示NULL）来解除cin与cout的绑定，进一步加快执行效率。
	int n,m,g;
	while(cin>>n>>m){
		BuildTree(1,1,n);
		rep(i,1,n){
			cin>>g;
			node[father[i]].value=g;
			UpdateTree(father[i]);
		}
		char ch;
		int a,b;
		while(m--){
			cin>>ch>>a>>b;
			if(ch=='Q'){
				cout<<QueryTree(1,a,b)<<endl;;
			}
			else{
				node[father[a]].value=b;
				UpdateTree(father[a]);
			}
		}
	}
	return 0;
}

测试数据：

6 5 
2 3 8 23 1 9
Q 1 6
S 2 3
Q 1 6
S 3 4
Q 1 6

测试结果：