并查集主要知识
什么是并查集?
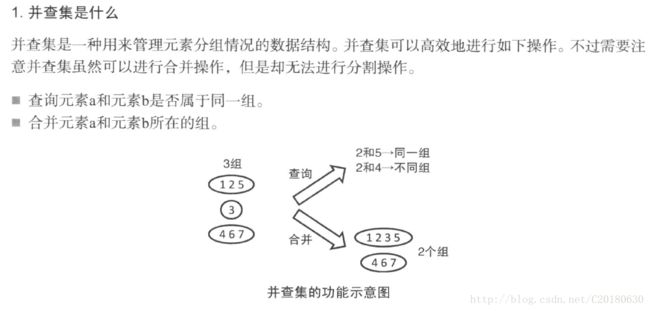
并查集是一种树型的高级数据结构,主要用于处理不相交集合的合并及查询问题。它在计算机科学中有着广泛的应用,例如求解最小生成树、亲戚关系的判定、确定无向图的连通子图个数、最小公共祖先问题等,都要用到并查集。
什么是集合?
集合是数学中最基本的构造之一,将一组满足某种性质的对象放在一起就形成了集合。集合中包含的对象称为集合中的元素,集合中的元素是无序而且唯一的。人们常用大写英文字母A、B、C等来表示集合,并用x∈A来表示x是集合A中的元素。
集合的并、交、差:
由A、B集合的全体元素组成的集合为A与B的并集,记作AUB;A与B的公共元素组成的集合称A与B的交集,记作A∩B;属于集合A而不属于集合B的元素组成的集合称为A减B的差,记作A-B。
如何实现存储集合中的元素?
由于集合中存放的是一组具有相同性质的对象,一般人很容易想到用数组来存储。用数组很容易实现集合类型,但要注意:因为数组一旦定义,其大小就固定不变。所以在定义的时候,要充分考虑最大空间。
也可以用链表来存储集合元素。链表可以很容易的动态生成和释放,所以增减节点是很方便的,完全不用考虑象数组那样的长度问题。删除元素也很方便。但是因为涉及到指针,实现起来很容易出错。
还可以用vector.它有数组的优点,而且又不必考虑数组那样可能越界的情况。
并查集的概念
在某些应用中,我们要检查两个元素是否属于同一个集合,或者将两个不同的集合合并为一个集合。这是不相交集合经常处理的两种操作:查找和合并,我们称为并查集。
并查集共有两个函数,root和union。
查找root:查找一个指定元素属于哪个集合.
合并union:将两个集合合并为1个集合。
除了这两个操作之外,还有一个基础的操作——makeset,用于建立只有1个元素的集合。
为了更精确的定义上述三个操作,我们需要用一种方法来表示集合。一种通用的做法是选择集合中某个固定的元素作为集合的代表,即该元素作为整个集合的唯一标识。一般说来,选取的代表是任意的。也就是说,到底选取集合中的哪个元素作为它的代表是无关紧要的。
在并查集中,我们对于集合的表示利用树的结构,一个集合表示为一棵树,树根即代表该集合的标识。如果两个元素在同一个树中,则它们是同一个集合;合并两个集合,即是对两棵树进行合并。
root(x):返回元素x所属集合的代表。为了判断任意两个元素x和y是否属于同一个集合,我们只需要判断root(x)和root(y)是否相等即可,如果相等,说明他们属于同一个集合,否则他们不属于同一个集合。
union(x,y):将包含元素x的集合(假设为Sx)和包含元素y的集合(假设为Sy)合并为一个新的集合(即这两个集合的并集),所得到并集可以用它的任何一个元素来做代表,一般我们都原来的某棵树的根作为合成的新树的根。
makeset(x):建立一个只包含元素x的集合,显然,此时该集合的代表应该而且只能为x.
并查集的实现(数组)
void makeset(x)
{
parent[x]=-1;
}parent[x]表示x的父亲编号.
最开始的,每个元素自成一个集合,即每个元素开始都当做一棵树,其父亲节点初始为-1,表示它没有父亲。
int root(x)//查找x所在的集合。
{
while(parent[x]!=-1)
x=parent[x];
return x;
}void myunion(int x,int y)
{
int r1=root(x);
int r2=root(y);
if(height[r1]>height[r2])
parent[r2]=r1;
else if(height[r1]else
{
parent[r1]=r2;
height[r2]++;
}
} 路径压缩
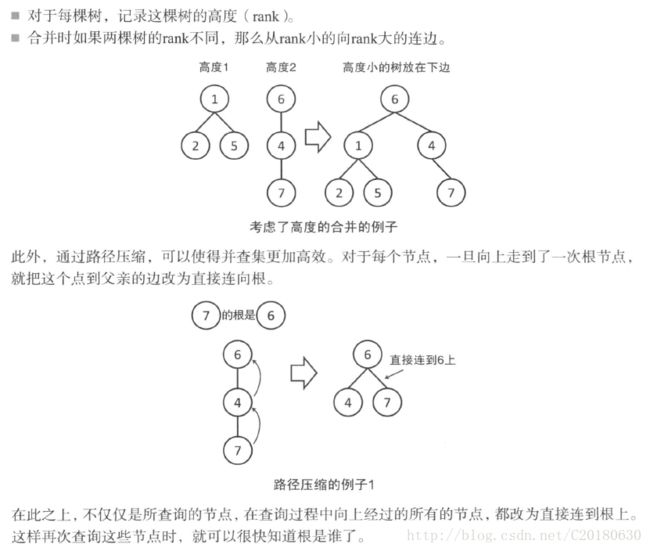
一个集合即是一棵树,在集合中,父子关系实际并不重要,其作用只是通过父亲找到树的根而已,而根也只是集合的标识,树中的任意节点都可以作根。在并查集的实现过程中,树的深度是影响速度的一个重要因素。树的深度越小,则root操作越快,union操作也越快。在union操作中,我们通过height数组已经尽量避免了树的高度增加。但是,我们还可以主动让树的高度减小。
改进后的root操作:
int root(int x)
{
if(parent[x]==-1)
return x;
else return parent[x]=root(parent[x]);
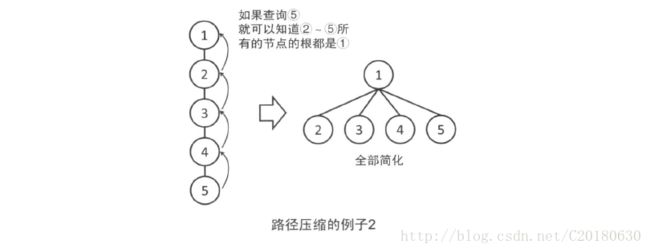
}这是路径压缩。它可以在find的过程中,让路径上的元素都成为根的儿子节点。这样,从形式上看,树就从细长型变成了扁平型。
使用路径压缩技术后,合并时不需要再使用height数组来判断两棵树谁高谁低了。
并查集的应用实例
亲戚
犯罪团伙
食物链
无所不在的宗教
改写kruscal算法
kruscal算法求最小生成树。
算法框架:
- 将所有边按小到大排序。
- 依次选取边,如果当前的边和之前选择的边不会形成环路,则选取当前边;若果形成环路,则不选择当前边。
- 循环执行2,直到选取的边的数目达到n-1条为止。
如何判断当前选择的边是否会和之前选择的边形成环路?
若当前选择的边的两个顶点为A,B,若A,B已经联通,则当前边必然导致回路;繁殖,若A,B本不连通,则当前边必然不会导致回路。
我们将联通的点作为一个集合,用并查集可以在logN时间内判断某两个点是否一个集合,也可以在logN时间内合并两个集合。
for(int i=1,j=0;iint t1=bian[j].v1,t2=bian[j].v2;
if(root(t1)!=root(t2)||root(t1)==root(t2)&&root(t1)==0){
i++;
ans+=bian[j].w;
union_set(t1,t2);
}
}