GZIP压缩原理分析（31）——第五章 Deflate算法详解（五22） 动态哈夫曼编码分析（11）构建哈夫曼树（03）

*构建distance树

现在已经知道压缩会在压缩结果中存储叶子节点深度信息（即码字长度）从而让解压方间接得到码表，但是问题来了，构造树的信息只包括码字长度，可解压方怎么知道这个码字长度是哪个原码的（注意，“原码”与“源码”的差别，前者是指原始数据，后者是指代码）？有什么方法可以让解压方以最简单的方式知道码字长度和原码的关系？带着这些问题，我们先来分析distance树。

 

查找缓冲区最大32KB（实际的代码实现中比这个要稍微小一些），也就是说，distance最大值就是32768，而且不能为0，所以distance的范围就是闭区间[1, 32768]。哈夫曼编码是根据字符出现频率自底向上构建哈夫曼树的，所以如果要构建distance树，那就要在[1, 32768]的范围内，根据不同的distance出现频率来构建一棵哈夫曼树，这棵树的叶子节点就是出现在当前待压缩数据中的distance值。假设待压缩数据比较大，那么其中的很多字符串都可以用长度距离对儿替换，也就是说，在[1, 32768]这个范围内的很多distance值都会成为长度距离对儿中的那个distance，如果让这些distance值全部参加哈夫曼树的构建，那这棵树要达到何种规模！举个例子，假设[1, 32768]范围内有一千个distance值成为了长度距离对儿中的那个“距离”，让这一千个distance值作为哈夫曼树的叶子节点，这棵哈夫曼树得有多大！为了避免这种情况的发生，压缩使用了一种特殊的处理方法，简化哈夫曼树的规模，同时优化压缩流程。

 

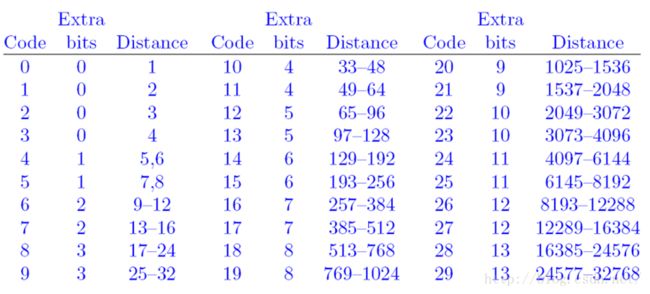
压缩将范围[1, 32768]细化为三十个规模不等的区间，每个区间容纳不同数量的distance值（这些distance值是连续的），并为这些区间编号。如下图所示，

图中Code列就是区间编号，简称区间码（十进制），范围是闭区间[0, 29]；Distance列是该区间所容纳的distance值范围；Extra bits列暂时不管，后面介绍。前四个区间，即区间码范围为闭区间[0, 3]的区间，都有且只有一个distance值；再往后，每个区间所容纳的distance个数逐渐增加。注意从区间码16开始，往后的每个区间所容纳的distance个数，都是128的倍数，这不是巧合，而是“刻意为之”，后面源码分析我们会看到这种倍数关系到底能带来什么好处！

 

有了这三十个区间，就可以避免直接对distance编码，因为压缩只会对这三十个区间的区间码进行编码。拿着LZ77之后的结果，判断结果中的distance值都分别落在了哪个区间，然后对这些区间的区间码进行哈夫曼编码即可。由于只有三十个区间，所以就算这三十个区间同时参与哈夫曼编码，那对应哈夫曼树也不会太大，更何况参与编码的区间如果达不到三十个的时候呢。

 

那问题来了，这三十个区间中，大部分的区间容纳的distance都不止一个，如果LZ77之后的结果中有很多不同的distance值都落到了同一个区间，怎么办？不是只对区间码进行哈夫曼编码么，现在咋办，怎么用这一个区间码把该区间下所有的distance值区分出来？上图中的Extra bits列就是用来解决这个问题的。Extra bits列表示“扩展位”，该列的值表示扩展位长度，仔细观察可以发现，扩展位长度与该区间容纳distance值个数是对应的（强调一下，其实没必要说吧~）。比如区间码4，该区间有两个distance，所以扩展位只有一位；区间码16，该区间有一百二十八个distance值，所以扩展位有七位。每个区间中的distance值都是连续的，所以扩展位表示的值从零开始到该扩展位能表示的最大值就可以将该区间中的每个distance编码。比如区间码5，扩展位长度是一，该区间容纳两个distance，所以distance_7的扩展值是0，distance_8的扩展值是1；区间码9，扩展位长度是三，该区间容纳八个distance值，所以distance_25的扩展值是二进制“000”，distance_26的扩展值是二进制“001”，distance_27的扩展值是二进制“010”……distance_31的扩展值是二进制“110”，distance_32的扩展值是二进制“111”。各区间容纳的distance值数量不同，换句话说就是各个区间的疏密程度不同。Distance值越小，区间划分越密；distance值越大，区间划分越稀疏。这还是与我们很早之前提到的那个“隐含假设”有关，相同的内容总是扎堆儿出现，越是小的distance值，其出现频率也就越高；出现频率越高的内容，其码字长度就应该尽可能的短。区间码的码字长度会因待压缩内容不同而不同，会依据实际情况变化；扩展值的长度是固定的，只会因所属区间不同而变化，遵照“隐含假设”所述，distance值越小，出现频率越高，所以扩展位长度越短，并且区间划分越密集。

 

哈夫曼编码是针对区间码进行的，因为编码结果是前缀码，所以经过哈夫曼编码后的区间码码字各不相同，都是唯一的，所以，用“区间码码字+扩展值”就可以唯一标识一个distance码字。比如区间4和区间9的哈夫曼编码码字分别为二进制“0010”和“0111”，distance_5的扩展值是二进制的“0”， distance_27的扩展值是二进制“010”，所以distance_5最终作为压缩结果的码字就是distance_5 = 0010 0，distance_27最终作为压缩结果的码字是distance_27 = 0111 010。这就是合成distance码字的规则，压缩/解压缩双方都知道这个规则。

 

Distance值的合成规则、扩展值的计算规则、distance区间码范围表，压缩/解压缩双方都知道，现在解压缩一方不知道的就是如何构造哈夫曼树从而把区间码码表得到。如果得到了区间码码表，再按照扩展值计算规则在解压缩本地把各区间的扩展值计算出来，就能够根据合成规则得到distance码表，对着distance码表就能把所有distance解码。我们已经知道压缩结果中存储的用于构建哈夫曼树的信息是码字长度，而哈夫曼编码又是针对区间码进行的，所以现在问题就聚焦在压缩结果怎么记录区间码的码字长度上。

 

区间码由[0, 29]这三十个连续的整数组成，假设一个有三十个元素的数组，这些区间码就是这个数组的下标，而数组元素就是下标对应的区间码码字长度，这样就可以把码字长度记录下来了。压缩结果记录区间码码字长度的方式基本就是这样，只不过没有“数组”这个实体，只是用的数组的“原理”。例如有如下码字长度序列，

0、0、1、2、3、3、0、0、0、0、0……（一共三十个数）

这几个数就是码字长度，而这几个数的排列顺序就是数组下标，数组下标就是对应的区间码。第0个数是0，相当于数组下标是0，数组元素也是0，所以区间码0的码字长度是0；第1个数是0，相当于数组下标是1，数组元素是0，所以区间码1的码字长度是0；第2个数是1，相当于数组下标是2，数组元素是1，所以区间码2的码字长度是1；第3个数是2，相当于数组下标是3，数组元素是2，所以区间码3的码字长度是2；第4个数是3，相当于数组下标是4，数组元素是3，所以区间码4的码字长度是3；第5个数是3，相当于数组下标是5，数组元素是3，所以区间码5的码字长度是3，以此类推，一直到第29个数，也就是区间码29的码字长度。这就是压缩结果记录区间码码字长度的方法。

 

前面我们依次分析了“对谁进行哈夫曼编码”、“如何合成实际的distance码字”以及“压缩结果如何记录构建树信息”的问题，现在我们介绍构建哈夫曼树以及得到区间码的哈夫曼编码码字的具体流程。

 

压缩只对区间码进行哈夫曼编码，也就是说，哈夫曼树的叶子节点最多也就三十个。落在区间中的distance数量就是该区间的区间码出现频率，利用出现频率自底向上构建哈夫曼树，构建过程和预备知识中的描述相同。此时构建的哈夫曼树是原始的哈夫曼树，如下图所示的哈夫曼树是有可能出现的，

我们说过，压缩使用的哈夫曼编码是范式哈夫曼编码，这样的树显然不符合范式哈夫曼编码的各个性质，不能用来编码。大家是否还记得这张图，

虽然原始哈夫曼树有可能（不排除构建的哈夫曼树恰好就是范式哈夫曼树）不符合范式哈夫曼树的性质，但各个叶子节点的深度，也就是码字长度，这两棵树都是相同的！压缩真正构建的哈夫曼树其实就是原始的哈夫曼树，这棵树的作用只有一个，就是计算各个叶子节点的深度，也就是计算出现在压缩结果中的那些区间码的码字长度（三十个区间，有可能仅有几个区间会参与哈夫曼编码，因为没有distance落入其他区间）。

 

得到了码字长度，就可以利用范式哈夫曼编码的性质来计算各个叶子节点的编码。范式哈夫曼编码的性质是固定的，树的形状也就基本固定了，保证树的右边的深度始终不小于左边即可，所以，利用码字长度计算码字的过程根本用不着再把范式哈夫曼树构建一遍，直接根据性质就可以把码字计算出来。比如对区间码2、4、5、6、7、8编码，这几个区间码的码字长度分别是1、3、3、3、4、4，码字长度为1的只有一个，码字长度为3的有三个，码字长度为4的有两个。公式“code = (code + bl_count[bits-1])<< 1”用来计算每层最左边那个节点的码字，code初始化为0，所以区间码2的码字是二进制“0”，区间码4的码字是二进制“100”，区间码7的码字是二进制“1110”；码字长度为3的码字有三个，第一个是“100”，第二个就是区间码5的码字，为“100+1 = 101”，第三个就是区间码6的码字，为“101+1 = 110”；码字长度为4的有两个，第一个是“1110”，第二个就是区间码8的码字，为“1110+1 = 1111”（这个例子不用深究，到源码分析时自然明白）。从这个过程中我们还可以看到一个细节，就是同一深度下，或者说同一码字长度下，最左边的叶子节点对应的区间码越小，越往右，叶子节点对应的区间码越大。

 

前面说了一大堆，其实构建哈夫曼树以及记录构建树信息的方法非常简单，只要保证这几个要点即可：

i.     压缩只针对区间码进行哈夫曼编码；

ii.    实际的distance码字由“区间码码字+扩展值”合成；

iii.   压缩结果只记录区间码的码字长度，各码字长度的排列序号就是该码字长度对应的区间码；

iv.   原始哈夫曼树各节点深度与范式哈夫曼树各节点深度相同；

v.    原始哈夫曼树只用来计算码字长度；

vi.   得到了码字长度就可以直接利用范式哈夫曼编码的性质计算码字，此时不用再构建树。

 

现在，我们为字符串“As mentioned above,there a(3,4)many kinds of wireless system(3,20)(4,42)than cellular.”中的distance编码。Distance值为4、20、42，对应区间码分别为3、8、10，每个区间码只出现了一次，构造哈夫曼树为

为了简便起见，这棵哈夫曼树是按照范式哈夫曼性质构建的，也就是实际的编码就会按照这棵树来进行。有没有觉得不太对劲？范式哈夫曼也好，原始哈夫曼也罢，叶子节点的深度是相同的，但是这里明显不对劲啊，按照我们前面的分析，区间码3应该和区间码8在同一层，为什么现在居然和区间码10在同一层呢？！而且为什么偏偏3和10的码字长度是二？这其实和源码中的build_tree过程以及pqremove宏有关，我们后续的源码分析章节会看到，这里只是给大家提前铺垫一下。

 

从这棵树中我们可以得到这三个区间码的哈夫曼编码（二进制）：

8     < ------------ >    0

3     < ------------ >    10

10   < ------------ >    11

现在根据distance区间码表对以上区间码内部的distance值进行扩展以及合成，

区间码extra bits     distance

8                3            17-24

3                0            4

10              4            33-48

 

合成的过程非常简单，先将区间码码字输出，紧接着输出扩展位编码即可。这里要注意一个问题，在接收压缩结果的这块内存上，以一个字节为例，区间码码字在该字节的低位，而扩展位编码在该字节的高位。如下图所示，

当然，实际情况中，一个distance码字有可能占用不了一个字节，也有可能一个字节都不够用，只要知道实际内存中，区间码码字在低位而扩展位编码在高位即可。

 

内存中存储的区间码码字与从树上算出的结果是不同的，是其按位逆序的结果。比如，上面区间码3的码字是二进制“10”，但是放到内存作为压缩输出结果时，就是“01”，即“10”按位逆序的结果。这个过程在源码分析时会看到实际的代码操作。

 

内存中存储扩展位编码的方式就是我们平时阅读的方式，这一点与区间码不同。比如，某扩展码是“100”，那么其作为压缩输出结果在内存中的存储方式仍然是“100”。

 

对区间码8进行扩展以及合成，distance值20

区间码码字          extra bits     distance       内存中的code

     0                       000               17                   000 0

     0                       001               18                   001 0

     0                       010               19                   010 0

     0                       011               20                   011 0

     0                       100               21                   100 0

     0                       101               22                   101 0

     0                       110               23                   110 0

     0                       111               24                   111 0

 

对区间码3进行扩展以及合成，distance值：4，

区间码码字          extra bits     distance        内存中的code

     10                      无                4                       01

 

对区间码10进行扩展以及合成，distance值42

区间码码字          extra bits     distance        内存中的code

     11                     0000              33                  0000 11

     11                     0001              34                  0001 11

     11                     0010              35                  0010 11

     11                     0011              36                  0011 11

     11                     0100              37                  0100 11

     11                     0101              38                  0101 11

     11                     0110              39                  0110 11

     11                     0111              40                  0111 11

     11                     1000              41                  1000 11

     11                     1001              42                  1001 11

     11                     1010              43                  1010 11

     11                     1011              44                  1011 11

     11                     1100              45                  1100 11

     11                     1101              46                  1101 11

     11                     1110              47                  1110 11

     11                     1111              48                  111111

那么到现在为止，LZ77结果中所有distance的码字就都得到了！如下表所示，

 

Distance 码表
Distance 值	Distance 码字（作为压缩结果）
4	01
20	011 0
42	1001 11

用码字替换实际的distance值，LZ77之后的那个字符串现在就是，

“As mentioned above,there a(3,01)many kinds ofwireless system(3,0110)(4,100111) than cellular.”。

 

别忘了，我们还要记录构建哈夫曼树的信息，三十个区间码，只有3、8、10的码字长度不为零，那么整个数列就是，

“0、0、0、2、0、0、0、0、1、0、2、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0、0”。这就是distance码字长度列。