线段树

本文转自：https://www.cnblogs.com/TheRoadToTheGold/p/6254255.html

目录

一、基本概念

二、线段树的基础操作

1、建树

2、单点查询（即查询一个点的状态，设待查询点为x）

3、单点修改（即更改某一个点的状态，对第x个数加上y）

4、区间查询（即查询一段区间的状态）

5、区间修改（即修改一段连续区间的值，给区间[a,b]的每个数都加x）

6、总结

---

 

一、基本概念

1、线段树是一棵二叉搜索树，它储存的是一个区间的信息。

2、每个节点以结构体的方式存储，结构体包含以下几个信息：

     区间左端点、右端点；（这两者必有）

     这个区间要维护的信息（事实际情况而定，数目不等）。

3、线段树的基本思想：二分。

4、线段树一般结构如图所示：

5、特殊性质：

由上图可得，

1、每个节点的左孩子区间范围为[l，mid]，右孩子为[mid+1,r]

2、对于结点k，左孩子结点为2*k，右孩子为2*k+1，这符合完全二叉树的性质

 

二、线段树的基础操作

 

注：以下基础操作均以引例中的求和为例，结构体以此为例：

struct node
{
    int l,r,w;//l，r分别表示区间左右端点，w表示区间和
}tree[4*n+1];

树记得开4倍空间。

线段树的基础操作主要有5个：建树、单点查询、单点修改、区间查询、区间修改。

 

1、建树

【主体思路】

a、对于二分到的每一个结点，给它的左右端点确定范围。

b、如果是叶子节点，存储要维护的信息。

 c、状态合并。

 

【代码】

void build(int l,int r,int k)
{
    tree[k].l=l;tree[k].r=r;
    if(l==r)//叶子节点 
    {
        scanf("%d",&tree[k].w);
        return ; 
    }
    int m=(l+r)/2;
    build(l,m,k*2);//左孩子 
    build(m+1,r,k*2+1);//右孩子 
    tree[k].w=tree[k*2].w+tree[k*2+1].w;//状态合并，此结点的w=两个孩子的w之和 
}

 

2、单点查询（即查询一个点的状态，设待查询点为x）

【主体思路】

与二分查询法基本一致，如果当前枚举的点左右端点相等，即叶子节点，就是目标节点。如果不是，因为这是二分法,所以设查询位置为x，当前结点区间范围为了l，r，中点为mid，则如果x<=mid，则递归它的左孩子，否则递归它的右孩子。

 

【代码】

void ask(int k)
{
    if(tree[k].l==tree[k].r) //当前结点的左右端点相等，是叶子节点，是最终答案 
    {
        ans=tree[k].w;
        return ;
    }
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) ask(k*2);//目标位置比中点靠左，就递归左孩子 
    else ask(k*2+1);//反之，递归右孩子 
}

 

3、单点修改（即更改某一个点的状态，对第x个数加上y）

【主体思路】

结合单点查询的原理，找到x的位置；根据建树状态合并的原理，修改每个结点的状态。

【代码】

void add(int k)
{
    if(tree[k].l==tree[k].r)//找到目标位置 
    {
        tree[k].w+=y;
        return;
    }
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) add(k*2);
    else add(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;//所有包含结点k的结点状态更新 
}

 

4、区间查询（即查询一段区间的状态）

【主体思路】

mid=(l+r)/2

y<=mid ,即 查询区间全在，当前区间的左子区间，往左孩子走

x>mid 即 查询区间全在，当前区间的右子区间，往右孩子走

否则，两个子区间都走

 

【代码】

void sum(int k)
{
    if(tree[k].l>=x&&tree[k].r<=y) 
    {
        ans+=tree[k].w;
        return;
    }
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) sum(k*2);
    if(y>m) sum(k*2+1);
}

 

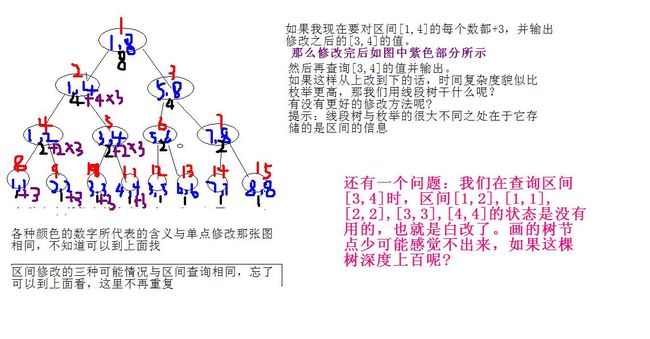
5、区间修改（即修改一段连续区间的值，给区间[a,b]的每个数都加x）

【主体思路】

 

为了实现这个，引入一个新的状态——懒标记。

       1、直观理解：“懒”标记，懒嘛！用到它才动，不用它就睡觉。

       2、作用：存储到这个节点的修改信息，暂时不把修改信息传到子节点。就像家长扣零花钱，你用的时候才给你，不用不给你。

       3、实现思路（重点）：

           a.原结构体中增加新的变量，存储这个懒标记。

           b.递归到这个节点时，只更新这个节点的状态，并把当前的更改值累积到标记中。注意是累积，可以这样理解：过年，很多个亲戚都给你压岁钱，但你暂时不用，所以都被你父母扣下了。

           c.什么时候才用到这个懒标记？当需要递归这个节点的子节点时，标记下传给子节点。这里不必管用哪个子节点，两个都传下去。就像你如果还有妹妹，父母给你们零花钱时总不能偏心吧

           d.下传操作：

                            ①当前节点的懒标记累积到子节点的懒标记中。

                            ②修改子节点状态。在引例中，就是原状态+子节点区间点的个数*父节点传下来的懒标记。

                            这就有疑问了，既然父节点都把标记传下来了，为什么还要乘父节点的懒标记，乘自己的不行吗？

                            因为自己的标记可能是父节点多次传下来的累积，每次都乘自己的懒标记造成重复累积

                         ③父节点懒标记清0。这个懒标记已经传下去了，不清0后面再用这个懒标记时会重复下传。就像你父母给了你5元钱，你不能说因为前几次给了你10元钱, 所以这次给了你15元，那你不就亏大了。 

     懒标记下穿代码：f为懒标记，其余变量与前面含义一致。

【代码】

懒标记下传：

void down(int k)
{
    tree[k*2].f+=tree[k].f;
    tree[k*2+1].f+=tree[k].f;
    tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
    tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
    tree[k].f=0;
}

区间修改：

void add(int k)
{
    if(tree[k].l>=a&&tree[k].r<=b)//当前区间全部对要修改的区间有用 
    {
        tree[k].w+=(tree[k].r-tree[k].l+1)*x;//(r-1)+1区间点的总数
        tree[k].f+=x;
        return;
    }
    if(tree[k].f) down(k);//懒标记下传。只有不满足上面的if条件才执行，所以一定会用到当前节点的子节点 
    int m=(tree[k].l+tree[k].r)/2;
    if(a<=m) add(k*2);
    if(b>m) add(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;//更改区间状态 
}

 

6、总结

加入懒标记后5种操作的总结。

#include
using namespace std;
int n,p,a,b,m,x,y,ans;
struct node
{
    int l,r,w,f;
}tree[400001];
inline void build(int k,int ll,int rr)//建树 
{
    tree[k].l=ll,tree[k].r=rr;
    if(tree[k].l==tree[k].r)
    {
        scanf("%d",&tree[k].w);
        return;
    }
    int m=(ll+rr)/2;
    build(k*2,ll,m);
    build(k*2+1,m+1,rr);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;
}
inline void down(int k)//标记下传 
{
    tree[k*2].f+=tree[k].f;
    tree[k*2+1].f+=tree[k].f;
    tree[k*2].w+=tree[k].f*(tree[k*2].r-tree[k*2].l+1);
    tree[k*2+1].w+=tree[k].f*(tree[k*2+1].r-tree[k*2+1].l+1);
    tree[k].f=0;
}
inline void ask_point(int k)//单点查询
{
    if(tree[k].l==tree[k].r)
    {
        ans=tree[k].w;
        return ;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) ask_point(k*2);
    else ask_point(k*2+1);
}
inline void change_point(int k)//单点修改 
{
    if(tree[k].l==tree[k].r)
    {
        tree[k].w+=y;
        return;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(x<=m) change_point(k*2);
    else change_point(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w; 
}
inline void ask_interval(int k)//区间查询 
{
    if(tree[k].l>=a&&tree[k].r<=b) 
    {
        ans+=tree[k].w;
        return;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(a<=m) ask_interval(k*2);
    if(b>m) ask_interval(k*2+1);
}
inline void change_interval(int k)//区间修改 
{
    if(tree[k].l>=a&&tree[k].r<=b)
    {
        tree[k].w+=(tree[k].r-tree[k].l+1)*y;
        tree[k].f+=y;
        return;
    }
    if(tree[k].f) down(k);
    int m=(tree[k].l+tree[k].r)/2;
    if(a<=m) change_interval(k*2);
    if(b>m) change_interval(k*2+1);
    tree[k].w=tree[k*2].w+tree[k*2+1].w;
}
int main()
{
    scanf("%d",&n);//n个节点 
    build(1,1,n);//建树 
    scanf("%d",&m);//m种操作 
    for(int i=1;i<=m;i++)
    {
        scanf("%d",&p);
        ans=0;
        if(p==1)
        {
            scanf("%d",&x);
            ask_point(1);//单点查询,输出第x个数 
            printf("%d",ans);
        } 
        else if(p==2)
        {
            scanf("%d%d",&x,&y);
            change_point(1);//单点修改 
        }
        else if(p==3)
        {
            scanf("%d%d",&a,&b);//区间查询 
            ask_interval(1);
            printf("%d\n",ans);
        }
        else
        {
             scanf("%d%d%d",&a,&b,&y);//区间修改 
             change_interval(1);
        }
    }
}