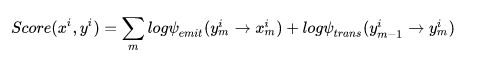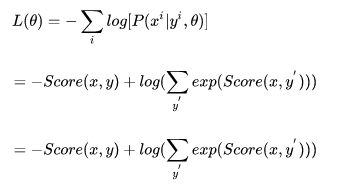序列标注：Bi-LSTM + CRF

最近在做序列标注的相关任务，为了理解bi-lstm + crf的原理及细节，找了很多相关资料，以及代码实现，这里分享给大家并附上一些自己的理解。

CRF

相关资料推荐

关于crf，我看了很多资料，这里推荐几个 - 英文的crf tutorial - 李航的统计学习方法 这两个讲的很细，公式很多，很多新入坑的小白看了肯定一头雾水,这里推荐一个知乎大神的回答，通俗易懂，有一些机器学习基础的都可以看懂。 - 知乎Scofield的回答

简单总结

这里我简单总结一下，以命名实体识别任务举例，我们有这样一组已标注的数据，B表示一个实体的开头，I表示当前词为命名实体的后面部分，O表示不是命名实体。

the(B) wall(I) street(I) journal(I) reported(O) today(O) that(O) apple(B) corporation(I) made(O) money(O)

很明显"the wall street journal"(华尔街日报)、"apple corporation"(苹果公司)为命名实体。

如果我们有这样一组已标注的数据

每个 x_i 是输入序列，y_i为一个标注序列

我们的目标是学习出一组条件概率分布模型， 即找到一组参数 theta

简单来说一组参数theta可以唯一确定一组模型，我们需要找到一组最优参数使得我训练数据中 x->y 的概率最大化。将上述最大化的目标函数取负，转化为最小化问题，即可用反向传播算法进行优化，找到近似最优参数theta。

好了有了目标就有了方向，下面的问题就是如何设计一个模型，对一个由x到y的序列映射进行打分（可以看做是可能性的大小），即上述公式中的Score(x, y)。在crf模型中我们有一个简单的假设，即当前输出的标签只和上一级输出的标签以及当前的输入有关，所以Score(x, y)应该由两部分组成，一个是转移特征概率，一个是状态特征概率。什么意思呢，转移特征概率是指前一个输出标签为 B 的前提下我当前输出标签为某个值比如 I 的概率大小。而状态特征是指我当前输入的词为 "wall" 的条件下，当前输出标签为某个值比如 I 的概率大小。

则Score(x, y)可以写成

最简单的，这里状态特征与转移特征都可以用一个矩阵来表示，这里矩阵中的参数值就是我们需要优化的theta。拿我们上面的举例的数据做例子（假设我们已知参数矩阵的值）：

• 转移特征

注：表示"start of sentence"，在输入序列开头加入这个标签我们便可以计算第一个词的转移概率，通常对于每个词的转移概率相同。

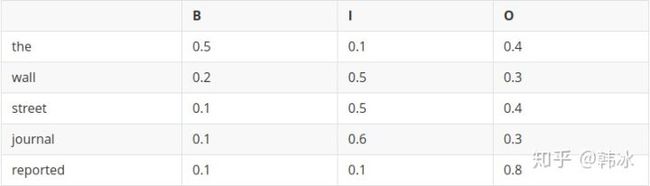
• 状态特征（这里只举几个词）

这里便可以算出

这里就不计算具体的值了。

BI-LSTM

相关资料推荐

• 介绍LSTM的一篇英文博客
• 吴恩达深度学习视频

简单总结

对于序列标注问题一个基于深度学习的方法便是BI-LSTM，简单的做法是将输入序列经过一个embeddig层转化为一个向量序列输入两个双向的LSTM单元，将每个时间序列的正向反向输出拼接，经过一个全连接层映射为一个维度为输出标签数量的一个向量，使用Softmax将输出归一化作为每种标签的概率。

LSTM（RNNs，不区分here）是依靠神经网络的超强非线性拟合能力，在训练时将samples通过复杂到让你窒息的高阶高纬度异度空间的非线性变换，学习出一个模型，然后再预测出一条指定的sample的每个token的label。

BI-LSTM + CRF

上述CRF的方式有什么问题呢？

最大的问题就是我们的前提假设，即当前输出的标签只和上一级输出的标签以及当前的输入有关。这显然与我们的经验不符，我们人在寻找一句话中的命名实体的时候显然是以整个句子作为上下文来判断的，在上述假设下我们显然丢失掉了很多上下文的信息，导致模型无法准确找出命名实体。

那单纯使用BI-LSTM不是可以有效学习到上下文关系吗？

但是这种方法有一个致命的缺陷，比如 "B" 的后面一定是 "I", 一定不是"B"，O"一定不会出现在两个"I"之间。由于没有状态转移的条件约束，模型很有可能输出一个完全错误的标注序列。这个错误在CRF中是不存在的，因为CRF的特征函数的存在就是为了对given序列观察学习各种特征（n-gram，窗口），这些特征就是在限定窗口size下的各种词之间的关系。用LSTM，整体的预测accuracy是不错, 但是会出现上述的错误：在B之后再来一个B。然后一般都会学到这样的一条规律（特征）：B后面接I，不会出现B。这个限定特征会使得CRF的预测结果不出现上述例子的错误。当然了，CRF还能学到更多的限定特征，那越多越好啊！

怎么解决这个问题呢？

经过上面的介绍，答案就很明显了，将Bi-lstm 与CRF的有点结合，取长补短。

在上面的章节中讲到，Score(x, y)可以分解为两个部分，一部分是状态特征，一部分是转移特征，现在转移特征不变，将BI-LSTM 的输出概率作为状态特征向量。即

这里ｈ为BI-LSTM 的输出，以本文的例子来说，是一个四维的向量，四个值分别代表(, B, I, O)的状态特征分数值，Ｐ为上文转移特征矩阵，公式中表示第标签从y_m-1 转移到ｙ_m的转移得分值。是不是很简单。

Implementation Detail

这里可以参考Pytorch官方Tutorial 的实现 Pytorch BI-LSTM + CRF Implemetation

计算损失函数

前面我们已经知道了给定模型和模型参数，如何计算出序列得分，即Score(x, y)，对于公式

这写错了：应该是P(y|x,theta)，在标注x和隐状态theta下，枚举状态序列y，让P(y|x,theta)最大

我们如何计算分母呢。有同学说，穷举出所有可能的 y`不就行了，但是这样做效率是很低的，算法的复杂度为 （其中N为标签的种类，T为序列的长度。)显然不可行, 那我们如何计算呢？我们将 P 带入我们的目标函数

下面的推导实际上就是如何把全部的y'都列出来，直接枚举肯定复杂度爆炸，推导实际上就是李航老师书上的后向算法，发现可以递归，推导中的2->t实际上表示的是子问题：

 

第一项很好求，我们来看第二项，假设序列的长度为t，输出标签种类为n，则

 

这个递推公式表名对于到第i+1个标签的路径，可以先把到第i个标签的logsumexp计算出来，先计算每一步的路径分数和直接计算全局分数相同，但这样可以大大减少计算的时间。

def _forward_alg(self, feats): # feats是 bi-lstm 的输出
        # Do the forward algorithm to compute the partition function
        init_alphas = torch.full((1, self.tagset_size), -10000.)
        # START_TAG has all of the score.
        init_alphas[0][self.tag_to_ix[START_TAG]] = 0.

        # Wrap in a variable so that we will get automatic backprop
        forward_var = init_alphas

        # Iterate through the sentence
        for feat in feats:
            alphas_t = []  # The forward tensors at this timestep
            for next_tag in range(self.tagset_size):
                # broadcast the emission score: it is the same regardless of
                # the previous tag
                emit_score = feat[next_tag].view(
                    1, -1).expand(1, self.tagset_size)
                # the ith entry of trans_score is the score of transitioning to
                # next_tag from i
                trans_score = self.transitions[next_tag].view(1, -1)
                # The ith entry of next_tag_var is the value for the
                # edge (i -> next_tag) before we do log-sum-exp
                next_tag_var = forward_var + trans_score + emit_score
                # The forward variable for this tag is log-sum-exp of all the
                # scores.
                alphas_t.append(log_sum_exp(next_tag_var).view(1))
            forward_var = torch.cat(alphas_t).view(1, -1)
        terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
        alpha = log_sum_exp(terminal_var)
        return alpha

结合代码还没看懂的同学，可以看一下我的手写推导过程(字丑):

 

维特比算法

模型训练完毕后我们如何预测新的数据呢，即给定一组未知标签的序列x，如何用我们的模型计算标签y呢？

我们的目标是对于所有可能的输出序列，找出一组序列y使得P(x|y)最大。即：

本质上是计算有向无环图的一条最大路径。粗暴地遍历所有的可能序列显然不行，时间复杂度为 $$ O(TN^T) $$ 此时维特比算法就派上用场了。其实质是用DP思想减少重复的计算。不过要说的是，Viterbi不是不是任何模型的专属，他只是恰好被满足了该问题的应用条件。这里上一个动图。

 

crf的独立性假设告诉我们当前step的输出只和前一个输出序列有关。

假定当我们从状态i进入状态i+1时，从S到状态i上各个节的最短路径已经找到，并且记录在这些节点上，那么在计算从起点S到第i+1状态的某个节点Xi+1的最短路径时，只要考虑从S到前一个状态i所有的k个节点的最短路径，以及从这个节点到Xi+1，j的距离即可。

还不太明白的同学可以参考李大雷的回答，这个回答大白话讲解维特比算法，再不懂的可以去补习下高中数学了。

def _viterbi_decode(self, feats):
        backpointers = []

        # Initialize the viterbi variables in log space
        init_vvars = torch.full((1, self.tagset_size), -10000.)
        init_vvars[0][self.tag_to_ix[START_TAG]] = 0

        # forward_var at step i holds the viterbi variables for step i-1
        forward_var = init_vvars
        for feat in feats:
            bptrs_t = []  # holds the backpointers for this step
            viterbivars_t = []  # holds the viterbi variables for this step

            for next_tag in range(self.tagset_size):
                # next_tag_var[i] holds the viterbi variable for tag i at the
                # previous step, plus the score of transitioning
                # from tag i to next_tag.
                # We don't include the emission scores here because the max
                # does not depend on them (we add them in below)
                next_tag_var = forward_var + self.transitions[next_tag]
                best_tag_id = argmax(next_tag_var)
                bptrs_t.append(best_tag_id)
                viterbivars_t.append(next_tag_var[0][best_tag_id].view(1))
            # Now add in the emission scores, and assign forward_var to the set
            # of viterbi variables we just computed
            forward_var = (torch.cat(viterbivars_t) + feat).view(1, -1)
            backpointers.append(bptrs_t)