给定一个含n(n≥1)个整数的数组,请设计一个在时间上尽可能高效的算法,找出数组中未出现的最小正整数。
笔者初涉《算法设计与分析》这门专业课,在做一些算法设计题的过程中遇到一些小感悟,特此记录和大家分享。
下面直接给出算法题目:
给定一个含n(n≥1)个整数的数组,请设计一个在时间上尽可能高效的算法,找出数组中未出现的最小正整数。例如,数组{-5, 3, 2, 3}中未出现的最小正整数是1;数组{1, 2, 3}中未出现的最小正整数是4。
笔者在看完这道题目后,进行了如下分析:
(1)题目要求算法时间上尽可能高效,因此采用空间换时间的办法。
(2)假定所给数组为arr[len],首先找到数组中的最大值MAX
2.1 若MAX <= 0 ,则数组中未出现的最小正整数为1
2.2若MAX>0,则开辟临时数组tempArr[MAX+1];
(3).遍历arr[len],如果arr[i]>0,则tempArr[arr[i]]=1,否则tempArr[arr[i]]=0;
(4).从i =1开始遍历tempArr[MAX+1],找到tempArr[i]=0,直接返回i,若tempArr[MAX+1]全为1,则说明数组中未出现的最小正整数为MAX+1
在以上分析中,可以发现使用临时开辟的额外空间tempArr[MAX+1]用于存储标记i=1到i=MAX+1的值。下面直接给出该算法的实现代码:
#include
using namespace std;
/**
* @author:陌意随影
* @date : 2020/2/27 11:54
* @todo:获取指定的数组的最大值
* @ parameter:
* @return:int
* @last change :
*/
int getMaxInteger(int arr[],int len) {
int max = arr[0];
for (int i = 1;i< len;i++)
{
if (max < arr[i]){
max = arr[i];
}
}
return max;
}
/**
* @author:陌意随影
* @date : 2020/2/27 12:00
* @todo:获取指定的数组未出现的最小的正整数
* @ parameter:
* @return:int
* @last change :
*/
int getMinInteger(int arr[],int len) {
int max = getMaxInteger(arr,len);
//最大值小于零书名该数组的未出现的最小的正整数为1
if (max <= 0){
return 1;
}else{
//开辟临时数组
int* tempArr = new int[max + 1];
//初始化临时数组
for (int i = 1; i <= max;i++) {
tempArr[i] = 0;
}
//遍历arr[len],如果arr[i]>0,则tempArr[arr[i]]=1,否则tempArr[arr[i]]=0;
for (int i = 0; i 0){
tempArr[arr[i]] = 1;
}
}
//从i =1开始遍历tempArr[MAX+1],找到tempArr[i]=0,直接返回i,若tempArr[MAX+1]全为1,则说明数组中未出现的最小正整数为MAX+1
for (int i = 1; i <= max;i++) {
if (tempArr[i] == 0){
return i;
}
}
return max + 1;
}
}
int main(){
int arr1[] = {-1,3,4,-2,2,-10,1,5,6};
//获取数组的最大值
cout <<"数组{-1,3,4,-2,2,-10,1,5,6}中未出现的最小正整数是:"<< getMinInteger(arr1,9) << endl;
int arr2[] = { 0,3,4,-2,2,1,1,5,454511111 };
cout << "数组{0,3,4,-2,2,1,1,5,454511111}中未出现的最小正整数是:" << getMinInteger(arr2, 9) << endl;
int arr3[] = { 1,3,4,2,0,888,1,5,6 };
cout << "数组{1,3,4,2,0,888,1,5,6}中未出现的最小正整数是:" << getMinInteger(arr3, 9) << endl;
system("pause");
}
在vs2017上运行测试:
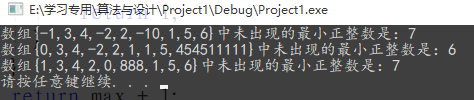
该算法的时间复杂度和空间复杂度都是: O(n);该方法存在很大的缺陷:比如当所给数组中的最大值MAX很大很大时,由于需要开辟额外的空间tempArr[MAX+1],容易造成程序运行时发生内存溢出的异常情况,相当消耗空间。这就说名程序还有可改进的空间,然后笔者又重新思考新的算法。
1.分配一个用于标记的数组temp[n],用来记录arr中是否出现了1~ n中的正整数,temp[0]对应正整数1,temp[n-1]对应正整数n,初始化temp中全部为0。
2.由于arr中含有n个整数,因此可能返回的值是1~ n+1,当arr中n个数恰好为1~n时返回n+1。
3.当数组arr中出现了小于等于0或者大于n的值时,会导致1~n中出现空余位置,返回结果必然在1到n中,因此对于arr中出现了小于等于0或者大于n的值可以不采取任何操作。
经过以上分析可以得出算法流程:
1.从arr[0]开始遍历arr,若0
3.若temp[i]全部不为0,返回i+1(跳出循环时i=n,i+1等于n+1),此时说明arr中未出现的最小正整数是n+1。
int getMinInterger2(int arr[],int len) {
int *temp = new int[len];
//初始化临时数组
for (int i = 1; i <= max;i++) {
temparrrr[i] = 0;
}
//遍历数组arr[len]给temp[len]赋标记值
for (int i = 0; i < len;i++) {
if (arr[i]>0&&arr[i]<=len){
temp[arr[i] - 1] = 1;
}
}
for (int i = 0; i < len;i++) {
//找到第一个满足temp[i]=0的下标i
if (temp[i]==0){
return i+1;
}
}
//说明temp[len]中的标记值全为1,也就是说arr[i]的值一一对应1
return len+1;
}
int main(){
int arr1[] = {-1,3,4,-2,2,-10,1,5,6};
//获取数组的最大值
cout <<"数组{-1,3,4,-2,2,-10,1,5,6}中未出现的最小正整数是:"<< getMinInteger2(arr1,9) << endl;
int arr2[] = { 0,3,4,-2,2,1,1,5,454511111 };
cout << "数组{0,3,4,-2,2,1,1,5,454511111}中未出现的最小正整数是:" << getMinInteger2(arr2, 9) << endl;
int arr3[] = { 1,3,4,2,0,888,1,5,6 };
cout << "数组{1,3,4,2,0,888,1,5,6}中未出现的最小正整数是:" << getMinInteger2(arr3, 9) << endl;
system("pause");
}
经过再次测试得出结果:

与第一种方法所得结果一致,说明该方法也是正确的。该算法的时间复杂度和空间复杂度都是: O(n);但在具体的运行时,第二种方法所需的实际空间和时间复杂度都小于第二种方法。比如拿一个例子来说:数组{0,3,4,-2,2,1,1,5,454511111}中元素个数len = 9, 最大值MAX=454511111
对于第一种方法额外需要开辟的空间为: temp[454511111],
第二种方法额外的需要开辟的空间为:temp[9],
显然第二种方法所需开辟的空间远远小于第一种方法所需要开辟的空间。
在给额外的数组赋值初始为0时,
for (int i = 0; i < len;i++) {
temp[i] = 0;
}
对于第一种方法for循环中所需遍历的次数为454511111次,而第二种方法所需要遍历的次数仅为len = 9;
在 找到第一个满足temp[i]=0的下标i 时,第一种方法的最坏情况是遍历 454511111 次,而第二种方法的最坏情况是遍历 9 次,第二种情况所需遍历次数远远小于第一种情况;综合分析知:
虽然两种方法的时间复杂度和空间复杂度均为O(n),但具体在计算机运行时,第二种算法所需额外空间和运行时间要比第一种算法少很多,从而第二种算法的资源消耗更小,在实际问题的解决中我们更倾向于使用第二种方法。
以上均为笔者的个人学习经验,若有错误和不足之前欢迎大家斧正。