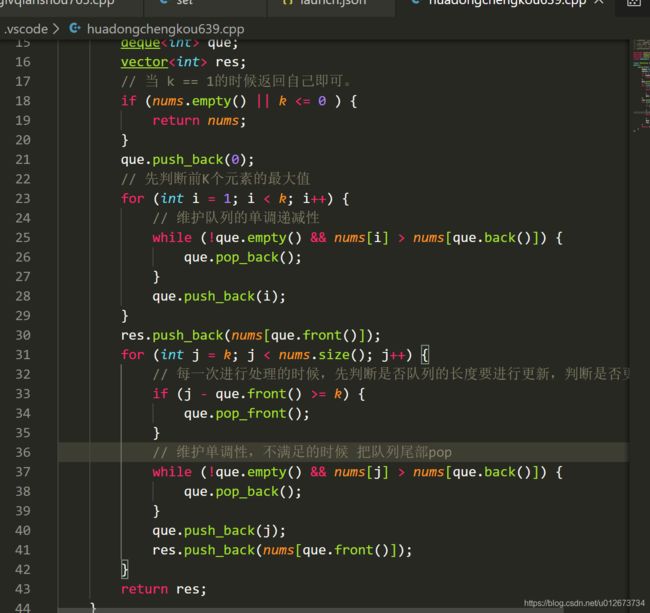
滑动窗口利用单调队列解题
滑动窗口和单调队列的应用
做本题的时候一定要自己想一些测试用例,边界条件的,针对队列的相反的,窗口为1,2,k的,本题思路比较清晰,就是维护一个最大size = k的单调递减的双端队列,考虑当入参 == 队列最后一个的时候怎么处理,因为每个元素都要进行进入队列和出队列,所以每次处理之前要先判断是否满足 que.size() <=k;不满足的时候说明左边窗口划过去了,pop出去首位。
单调队列
力扣 239 滑动窗口
239. 滑动窗口最大值
难度困难328
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
题解:
// 尝试维护一个单调队列的方式去更新最大值
// 使用双向队列,建议大家熟悉下双端队列的增删排序遍历操作
// 本文用的有 首部添加:.push_front(x) 查看首部:.front(), 剔除 .pop_front()
// 尾部添加: .push_back(i), 查看尾部 .back(), 剔除 .pop_back()
// 此题维护单调递减,当破坏单调性的时候,从队列尾部进行向前pop,并维护K这个范围
// 尝试维护一个单调队列的方式去更新最大值
// 使用双向队列,建议大家熟悉下双端队列的增删排序遍历操作
// 本文用的有 首部添加:.push_front(x) 查看首部:.front(), 剔除 .pop_front()
// 尾部添加: .push_back(i), 查看尾部 .back(), 剔除 .pop_back()
// 此题维护单调递减,当破坏单调性的时候,从队列尾部进行向前pop,并维护K这个范围
#include
#include
#include
using namespace std;
class Solution {
public:
vector
deque
vector
// 当 k == 1的时候返回自己即可。
if (nums.empty() || k <= 0 ) {
return nums;
}
que.push_back(0);
// 先判断前K个元素的最大值
for (int i = 1; i < k; i++) {
// 维护队列的单调递减性
while (!que.empty() && nums[i] > nums[que.back()]) {
que.pop_back();
}
que.push_back(i);
}
res.push_back(nums[que.front()]);
for (int j = k; j < nums.size(); j++) {
// 每一次进行处理的时候,先判断是否队列的长度要进行更新,判断是否更新窗口
if (j - que.front() >= k) {
que.pop_front();
}
// 维护单调性,不满足的时候 把队列尾部pop
while (!que.empty() && nums[j] > nums[que.back()]) {
que.pop_back();
}
que.push_back(j);
res.push_back(nums[que.front()]);
}
return res;
}
};
}