算法班小结

Chapter 2: Binary Search & LogN Algorithm

时间复杂度分析

O(1)
O(logn)	二分法
O(sqrt n)	分解质因数
O(n)	高频
O(nlogn)	排序
O(n^2)	数组，枚举，动规
O(n^3)	数组，枚举，动规
O(2^n)	组合有关搜索
O(n!)	排列有关搜索

 

根据时间复杂度倒推算法是面试中的常用策略

 

二分法模板

start + 1 < end
start + (end - start) / 2
A[mid] ==, <, >
A[start] A[end] ? target

1. 任意位置 VS 2. 第一个位置 VS 3. 最后一个位置

1. Classical Binary Search
2. First Position of Target
3. Last Position of Target

 

二分位置 之 OOXX

找到满足某个条件的第一个位置或者最后一个位置

1. First Bad Version
2. Find K closest Elements
3. Find Minimum in Rotated Sorted Array
   1. First Position <= Last Number
   2. Follow up: repeated number? Not guarantee in log(n) time
   3. 最坏情况下需要把每个位置上的值都看一遍
4. Maximum number in mountain sequence

倍增法 (Exponential Backoff)

int r = 1;
while (r < limit){
    r = r << 1;
}

使用到倍增思想的场景： 动态数组

1. Search in a big sorted array

相关练习

1. Search a 2D Matrix II
2. Search for a Range
3. Smallest Rectangle Enclosing Black Pixels

 

二分位置之 保留一半

保留有解的一半，或者去掉无解的一半

1. Find Peak element
2. Search in rotated Sorted Array

LogN 算法

1. Fast Power
2. Pow (x,n)

 

Chapter 3 Two Pointers Algorithm

同向双指针

两指针一前一后，直到前面的指针走过头 O(n)

1. Move zeros
2. window sum
3. remove duplicate numbers in array
4. intersection of two linked lists
5. linked list cycle
6. linked list cycle II

相向双指针

两根指针一头一尾，向中间靠拢直到相遇 O(n)

Reverse 类

1. Valid Palindrome
2. Valid Palindrome 2 可以删掉一个字符

Two sum 类

1. Two sum input array is sorted
2. Two sum – unique pairs
3. 3Sum
   1. 统计所有的和为 0 的三元组
4. Triangle Count
5. Two sum – Closest to Target
6. 3Sum Closest
7. two sum data structure design 只能使用hashmap
8. 4Sum
9. two sum difference equals to target

对于求两个变量如何组合的问题，可以循环其中一个变量，然后研究另外一个变量如何变化

Two sum 计数问题

1. Two sum less than or equal to target
2. Two sum greater than or equal to target

Partition 类

While left <= right:
    While left <= right and nums[left]在左侧：
        left+=1
    While left <= right and nums[right]在右侧: 
        right-=1
    If left <= right: 
        swap,
        left+=1,right-=1;

1. Partition array O(n)
2. Quick Sort
3. Quick Select (Kth largest element)
4. Partition Array by Odd and Even
5. Interleaving Positive and Negative Numbers
6. Sort Letters by Case
7. Sort Colors
8. Sort Colors II (K colors,Rainbow Sort O(nlogk)
9. pancake sort

 

三指针算法 (3-way partition)

一个指针循环，维护一个头指针指向第一个区域的边界，维护一个尾指针指向第三个区域的边界

void threeWayPartition(vector &nums, int low, int high) {
    int i = 0;
    int j = 0;
    int n = nums.size()-1;
    
    while(j <= n){
        if(nums[j] < low){
            swap(nums[i],nums[j]);
            i++;
            j++;
        }else if(nums[j] > high){
            swap(nums[j],nums[n]);
            n--;
        }else{
            j++;
        }
    }
}

1. Sort Colors

2. Partition Array II

 

Chapter 4 BFS & Topological Sorting

什么时候应该使用BFS？

BFS 空间由宽度决定：最多叶结点进队列 n/2. O(n)

图的遍历Traversal in Graph

• Level Order Traversal
• Connected Component
• Topological Sorting

 

最短路径Shortest Path in Simple Graph

• 仅限简单图求最短路径(每条边长都相等或等于1)

 

非递归方式找所有方案Iteration solution for all possible results

 

题型与算法的对应关系

最短路径

简单图-> BFS

复杂图 ->Dijkstra

最长路径

图可以分层 -> Dynamic programming

图不能分层 -> DFS

 

BFS in Binary Tree

Time: O(n)

1. Binary Tree Level Order Traversal
   1. 主要数据结构 Queue， 算法需要分层
2. Binary-tree serialization
3. Binary tree level order traversal ii
4. Binary Tree Zigzag Order Traversal
5. Convert Binary Tree to Linked Lists by Depth

BFS in Graph

Time: O(V+E) V个点，E条边

需要使用unordered_map 来储存访问过的节点(进过queue的)

图中存在环，同一个节点可能重复进入队列

1. Clone Graph
2. Word Ladder
   1. Implicit graph 最短路径
3. graph valid tree
4. search graph nodes
5. connected component in undirected graph

BFS in Matrix

Time: O(R*C) R行C列, R*C个点，R*C*2 条边

1. Number of Islands
2. Knight shortest path
3. zombie in matrix
4. build post office II

Topological Sorting

用BFS做

1. Topological Sorting
2. Course Schedule I && II
3. Alien Dictionary
4. Sequence reconstion
   1. 判断是否只有一个拓朴排序

方法：

1. 统计每个点的入度
2. 将每个入度为0的点放入QUEUE 作为起始节点
3. 不断从队列中拿出一个点，去掉这个点的所有连边，其他点的相应的入度-1
4. 一旦发现新的入度为0的点，丢回队列中

用DFS做方法：

// O(n)
// two states: VISITING,VISITED
for each node:
    if not marked:
        if(dfs(node) == CYCLE) return CYCLE
return OK

dfs(node):
    if node is VISITED: return OK
    if node is VISITING: return CYCLE
    make node as VISITING
    for each new_node in node.neighbors:
        if dfs(new_node) == CYCLE: return CYCLE;
    make node as VISITED
    add node to the head of ordered_list
    return OK

四种问法

1. 求任意一个拓扑序
2. 问是否存在拓扑序
3. 求所有的拓扑序
   1. DFS
4. 求是否存在且仅存在一个拓扑序
   1. QUEUE中最多同时只有一个节点

 

Chapter 5 Binary Tree & Tree-based DFS

二叉树

二叉树 最多2^h -1个结点

节点为N的二叉树，共有N个子树

二叉树高度 O(n)

heap, balanced BT(AVL,red-black-tree) 高度 O(logn)

二叉树考点剖析

Tree based DFS

DFS 空间由深度决定

1. subtree with maximum average
2. invert binary tree
3. validate binary search tree

 

 

第一类考察形态：求值，求路径类二叉树问题

maximum/minimum/average/sum/paths

1. Minimum subtree   (分治法 或分治+traversal（和全局变量打擂台))
2. Binary Tree Paths  (Traversal)
3. Lowest Common Ancestor    (分治：左右子树）
   1. follow up LCA III (nodes may not exist => multiple returns record the existence of each node)
4. Subtree with maximum average

第二类考察形态：结构变化类二叉树问题

1. Flatten Binary Tree to Linked List (Traversal,分治）
2. Invert binary tree

第三类考察形态：二叉搜索树类问题

BST 问题很可能涉及到iterator （inorder traversal）必用stack

1. Kth smallest element in BST
   1. inorder traversal (iterator)
   2. space:O(h), time O(k+h)
   3. follow up: 二叉树经常被修改 用hashmap 储存某个节点为代表的子树的节点个数
2. Binary Search Tree Iterator
   1. stack 中保存一路走到当前节点的所有节点
   2. stack.peek() 一直指向 iterator 指向的当前节点
   3. hasNext() 只需要判断 stack 是否为空
   4. next() 只需要返回 stack.peek() 的值，并将 iterator 挪到下一个点，对 stack 进行相应的变化
   5. 挪到下一个点的算法如下：
      • 如果当前点存在右子树，那么就是右子树中“一路向西”最左边的那个点
      • 如果当前点不存在右子树，则是走到当前点的路径中，第一个左拐的点
3. Closest Binary search Tree Value
   1. inorder traversal
   2. lowerbound/upperbound
4. Validate binary search tree
5. Inorder successor in binary search tree
6. Search range in binary search tree
7. Insert node in a binary search tree
8. Remove node in binary search tree

BST基本性质

定义：

• 左子树都比根节点小
• 右子树都不小于根节点

效果：

• in-order traversal是不下降序列

性质：

• 如果 in-order traversal 不是不下降序列，则一定不是BST
• 如果一棵二叉树 in-order traversal 是不下降，也未必是BST

 

Chapter 6 Combination based DFS

碰到让你找所有方案的题，基本可确定z是 DFS 除了二叉树以外的90% DFS的题，要么是排列，要么是组合

组合问题用start index标记是否妨问过

组合搜索问题Combination （traversal）

• 问题模型：求出所有满足条件的“组合”。
• 判断条件：组合中的元素是顺序无关的。
• 时间复杂度：与2^n相关。

 

递归三要素

一般来说，如果面试官不特别要求的话，DFS都可以使用递归(Recursion)的方式来实现。

递归三要素是实现递归的重要步骤：

• 递归的定义
• 递归的拆解
• 递归的出口

1. Combination Sum

   1. 与Subsets比较

      Combination Sum限制了组合中的数之和

      加入一个新的参数来限制

      Subsets无重复元素，Combination Sum有重复元素

      需要先去重

      Subsets一个数只能选一次，Combination Sum一个数可以选很多次

      搜索时从index开始而不是从index + 1

2. Combination Sum II
3. k Sum II
4. Palindrome Partitioning
   1. O(2^(n-1)*n) worst time
5. Split String 

 

通用的DFS时间复杂度计算公式

O(答案个数*构造每个答案的时间)

 

1. Wildcard Matching
2. Regular Expression Matching
3. Split string
4. Word Break II

记忆化搜索 （memoization search）分治

有重复节点，节省计算

主要还是dfs但是用hashmap存了已经经过的节点。有动规的思想在里面

 

Chapter 7 Permutation based DFS

Permutation

问题模型：求出所有满足条件的“排列”。

判断条件：组合中的元素是顺序“相关”的。

时间复杂度：与n! 相关。

O(答案个数 * 构造答案） = O(n! * n)

排列问题用visited标记是否访问过

1. String Permutation II
   1. 去重（选代表，第一个不一样的，后面一样的只有前面都选了才能选）
   2. sort is necessary
2. N Queens
   1. 斜线攻击条件（x1+y1 == x2+y2 或x1-y1 == x2-y2)
   2. 优化 is_valid 成为 O(1) 用一个visited记录col, sum, diff,后两个是对角线攻击
3. Next closest time
4. next permutation
5. permutation index

 

Graph-based Depth-first Search

1. Letter Combinations of Phone Number
2. follow up
   1. 如果有个词典，要求组成的单词都是词典里的，如何优化

Word 四兄弟

1. Word break
2. Word Ladder II
   1. DFS+BFS 所有，最短路径
   2. BFS 从end 到 start 记录到终点距离数组
   3. 起点开始DFS
3. Word Search II
   1. hash map or Trie
4. Word Pattern II
   1. 匹配字符串，DFS

 

Chapter 8 Stack, Queue, Hash & Heap

数据结构类面试问题的三种考法

数据结构可以认为是一个数据存储集合以及定义在这个集合上的若干操作（功能）

他有如下的三种考法：

考法1：问某种数据结构的基本原理，并要求实现

例题：说一下Hash的原理并实现一个Hash表

考法2：使用某种数据结构完成事情

例题：归并K个有序数组

考法3：实现一种数据结构，提供一些特定的功能

例题：最高频K项问题

 

数据结构时间复杂度的衡量方法

数据结构通常会提供“多个”对外接口

只用一个时间复杂度是很难对其进行正确评价的

所以通常要对每个接口的时间复杂度进行描述

 

数据结构设计类问题

比如你需要设计一个 Set 的数据结构，提供 lowerBound 和 add 两个方法。lowerBound

的意思是，找到比某个数小的最大值

算法1：O(n) lowerBound O(1) add

使用数组存储，每次打擂台进行比较，插入就直接插入到数组最后面

算法2：O(logn) lowerBound O(logn) add

使用红黑树（Red-black Tree）存储 C++里的map

不一定谁好谁坏！要看这两个方法被调用的频率如何。

如果lowerBound很少调用, add非常频繁,则算法1好。

如果lowerBound和add调用的频率都差不多，或者lowerBound被调用得更多，则算法2好

不过通常来说，在面试中的问题，我们会很容易找到一个像算法1这样的实现方法，其中一个操作时间复杂度很大，另外一个操作时间复杂度很低。

通常的解决办法都是想办法增大较快操作的时间复杂度来加速较慢操作的时间复杂度。

 

队列Queue

支持操作：O(1) Push / O(1) Pop / O(1) Top

队列的基本作用就是用来做BFS

1. Moving Average from Data Stream

 

栈Stack

支持操作：O(1) Push / O(1) Pop / O(1) Top

非递归实现DFS的主要数据结构

 

哈希表Hash

支持操作：O(1) Insert / O(1) Find / O(1) Delete

问：这些操作都是O(1)的前提条件是什么？

任何操作的时间复杂度从严格意义上来说都是O(keySize)而不是O(1)

整数可以说O(1),但字符串不行，字符串可能很长。

 

Hash Table, Hash Map 和 Hash Set的区别

什么是Hash Function (产生HashCode的函数)，作用以及实现原理

什么是Open Hashing

什么是Rehashing（重哈希）

 

1. LRU Cache
   1. 因为要快速删除中间元素，所以想到链表
   2. LinkedHashMap = LinkedList + HashMap
   3. ListNode with key, value,next
   4. Hash中存储Singly List中的prev node即可
2. Insert Delete GetRandom O(1)
   1. 只有数组能随机访问
   2. 删除后得空位后面元素补
   3. 哈希表key=number，value = index
3. First Unique Character in a String
   1. 不用额外空间，用时间复杂度增加
   2. 哈希表
   3. 限制一遍遍历
4. first unique number in a stream II
   1. data stream
   2. 保存到目前为止unique number 列表
   3. linked list + hash_map +hash_set
   4. hash: key= value, val = prev node, hashset 记录有没有出现过

Related Questions

1. Subarray sum
2. Copy List with random pointer
3. Anagrams
4. Longest consecutive sequence

Heap

支持操作：O(log N) Add / O(log N) Remove / O(1) Min or Max

Max Heap vs Min Heap

Heap 加了哈希表实现了remove O(logN)

priority_queue: remove O(N)

 

1. Ugly Number II
   1. 每个丑数都是前面一个丑数×2，x3，x5得到
   2. 用heap O(nlogn)
2. Merge K Sorted Lists
   1. priority_queue: O(Nlogk)
   2. 两两归并，像一个树一样 也是O(Nlogk)
   3. 归并排序，分治法还是 O(Nlogk) 然后用merge two sorted lists (leetcode 超时？？？）
3. K closest Points
4. Top K largest number II
   1. online 算法 maxHeap=> O(nlogn+klogn) 建堆 heapify O(n) 或者 O(nlogn), 然后pop k次
   2. minHeap of k elements O(nlogk) 再sort O(klogk)

Top K problem

1. Quick select O(n)
2. heap 在线算法

Related Questions

1. high five
2. merge k sorted arrays
3. data stream median
4. top-k largest numbers
5. kth smallest number in sorted martix

 

Chapter 9 Interval,Array, Matrix & Binary Indexed Tree

• Merge Two / K Sorted Arrays / Intervals相关算法即拓展题
• Median of Unsorted / Two Sorted / K Sorted Arrays相关算法及拓展题
• 通过Range Sum Query学习Binary Indexed Tree

1.  Merge Two Sorted Arrays
   1. 思想就像简易版merge k sorted lists
2. merge sorted array
   1. 把小数组merge到有足够空余空间的大数组里
   2. 空余位置在尾巴上，大的数组往后面丢
3. merge two sorted interval lists
   1. 按区间左端点排列
   2. 重点在于 merge function， merge function 传入 result 和 cur interval就够。 last intervel可以从 result 中最后一个interval取得。比较当前区间的头和last区间的尾然后看看需不需要合并，不合并直接推入result，合并，直接更改last的 end
4. merge k sorted arrays
   1. K路归并算法（外排序算法 External sorting）
5. merge k sorted interval lists
   1. merge k sorted arrays + merge two sorted interval lists

extra space = extra memory = 不包含输入和输出的算法耗费得额外空间

1. Intersection of two arrays
   1. 从O(min(n,m))space 降到O(1) space
   2. 先排序两个array 然后用binary search 在第一个array里找第二个array每一个数
   3. O(nlogn + mlogm +mlogn)
2. intersection of two arrays ii
   1. 先排序再merge two sorted arrays
   2. 哈希表
3. intersection of arrays
   1. 先sort每个array
   2. 再用pq类似merge k sorted arrays
4. Sparse Matrix Multiplication
   1. 一般矩阵乘法O(n^3) =>O(n*n*x)
   2. 每个矩阵变成行向量,列向量 O(n*n) 把非0位拿出来，存入非0位得坐标至向量
   3. 第一个矩阵列坐标和第二个矩阵行坐标相等得乘一下加起来

Median

求数组的中位数

Follow up I:没排序数组的第k大

用我们之前学过的Quick Select算法就可以

1. Median of two sorted arrays
   1. find median = find kth (k=n/2)
   2. O(1)时间把 k 问题变成 k/2 问题 => O(logk)
2. median of k sorted arrays
   1. 二分答案
   2. O(k) start = min{},end = max{}
   3. mid = x    第一个number   count of (<=x) >= （N+1）/2 是中位数
   4. 每个数组 count of (<=x) 也是用二分 O(klogn)
   5. O(logR klogn)
3. 假如K个排序数组位于不同的机器上如何利用机器的并发性提高算法效率？
   1. 每个数组 count of (<=x)这部分二分可以并发

 

1. Best Time to Buy and Sell Stock
   1. prefix sum (贪心）
   2. 等同于 maximum subarray 当前值减去之前得最小值
2. Submatrix Sum
   1. 把submartix 转化为 subarray
   2. 做prefix sum在row 方向上
   3. 上下边界搭配 （可能性 O(n^2)）
   4. 根据上下边界用prefix sum得到一个一维数组
   5. 一维数组左右边界之间等于0 用prefix sum相等 （subarray sum）
3. Maximum Submatrix
   1. 类似上一题
   2. 转化为1维array后用maximum subarray做

 

Binary Indexed Tree 树状数组

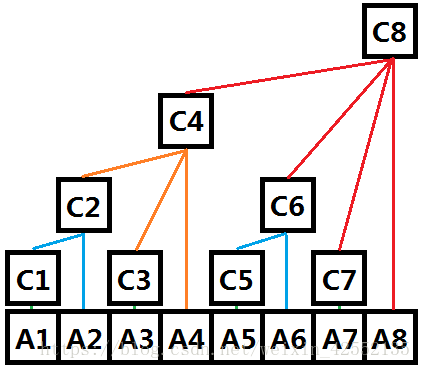
数组在物理空间上是连续的，而树是通过父子关系关联起来的，而树状数组正是这两种关系的结合，首先在存储空间上它是以数组的形式存储的，即下标连续；其次，对于两个数组下标x，y(x < y)，如果x + 2^k = y (k等于x的二进制表示中末尾0的个数)，那么定义(y, x)为一组树上的父子关系，其中y为父结点，x为子结点。(4的二进制表示为"100"，所以k=2，那么4 + 2^2 = 8，（8,4）一定是树上的父子关系）

我们定义C[i]的值为它的所有叶子结点的权值 的总和。根据上述逻辑结构和思想，可以写出C[i]的表达式，C[i]=A[i]+A[i-1]+....+A[i-2^k+1]。k代表i的二进制的最后连续0的个数。

其实C[i]还有一种更加普适的定义，它表示的其实是一段原数组A的连续区间和。区间的左端点为i - 2^k + 1，右端点为i。

构建树状数组，实则就是初始化C数组。对于C数组，我们知道，下标为i的Ci，在树形逻辑结构中，它的父亲是i + 2^k = y，而它父亲的父亲则是y + 2^ k' = m...一直到超出数据范围为止。也就是说，原本的Ai，只会影响Ci及Ci的祖先。

 

基于“前缀和”信息来实现:

• Log(n)修改任意位置值
• Log(n)查询任意区间和

功能特性：

对于一个有N个数的数组，支持如下功能：

update(index, val) // logN 的时间内更新数组中一个位置上的值

getPrefixSum(k) // log(K) 的时间内获得数组中前K个数的和

问：如何用 getPrefixSum(k) 实现 getRangeSum(x, y) ?

实现特性：

虽然名字叫做Tree，但是是用数组（Array）存储的

BIT是一棵多叉树，父子关系代表包含关系

BIT的第0位空出来，没有用上

如何求前缀和？

由前面可知，C[i] = A[i - 2^k + 1] + A[i - 2^k + 2] +... + A[i]，所以

sum(i) = A[1] + A[2] + ... + A[i] 
       = A[1] + A[2] + ... + A[i - 2^k] + A[i - 2^k + 1] + ... + A[i]
       = A[1] + A[2] + ... + A[i - 2^k] + C[i]
       = sum(i - 2^k) + C[i]
       = sum(i - lowbit(i)) + C[i]

如何更新？

 

BIT的两个操作总结

getPrefixSum(x)

不断的做 x = x - lowbit(x)直到 x = 0

update(x,val)

• 计算出 delta = val - A[x] 也就是增量
• 从x开始，不断的将 BIT[x] += delta,然后 x = x + lowbit(x),直到 x > N

void update(int index, int val){
    int delta = val - A[index];
    A[index] = val;
    
    for(int i = index + 1; i <= arr.size(); i += lowbit(i)){
        BIT[i] += delta;
    }
}

int getPrefixSum(int index){
    int sum = 0;
    for(int i = index + 1; i > 0; i -= lowbit(i)){
        sum += BIT[i];
    }
    return sum;
}

int lowbit(int x)
    return x & (-x);

Binary Indexed Tree 总结

Binary Indexed Tree 事实上就是一个有部分区段累加和数组
把原先我们累加的方式从：
for (int i = index; i >= 0; i = i - 1) sum += arr[i];
改成了
for (int i = index+1; i >= 1; i = i - lowbit(i)) sum += bit[i];
 

 

首先我们必须明确的事情是，树状数组只能维护前缀(前缀和，前缀积，前缀最大最小)，而线段树可以维护区间。我们求区间和，是用两个前缀和相减得到的，而区间最大最小值是无法用树状数组求得的。(经过一些修改处理，也可以处理)

所以树状数组可以针对的题目是：
1.如果问题带有区间和，或者可以转化成区间和问题，可以尝试往树状数组方向考虑

• 从面试官给的题目中抽象问题，将问题转化成一列区间操作，注意这步很关键

2.当我们分析出问题是一个区间和的问题时，如果有以下特征：

• 对区间的单个元素进行修改操作
• 对区间进行求和操作

3.我们就可以套用经典的树状数组模型进行求解

什么情况下，无法使用树状数组？
首先，线段树无法处理的问题树状数组也无法处理。其次，对于区间最大值这类无法通过两个区间相减操作得到解答的问题，树状数组一般也无法处理。（即经过一些修改处理，也可以处理）

那么相比较于线段树，为什么选择树状数组？
1.更好写（lowbit函数、add函数、sum函数构成树状数组的核心，共计十余行左右）
2.更快（树状数组运用位运算、不递归）
3.更少空间（树状数组只有O(n)的空间消耗，线段树根据写法和实现不同空间消耗也有所不同，但都大于树状数组的消耗

 

1. Range Sum Query Immutable
2. Range Sum Query 2D Immutable
3. Range Sum Query Mutable
4. Range Sum Query 2D Mutable
5. Count of Smaller Number before itself
   1. 基于“值的范围”构建Binary Indexed Tree是一种常见策略
6. Reverse Pairs