网易2020校招笔试- 系统开发/研发工程师（提前批）算法题题解

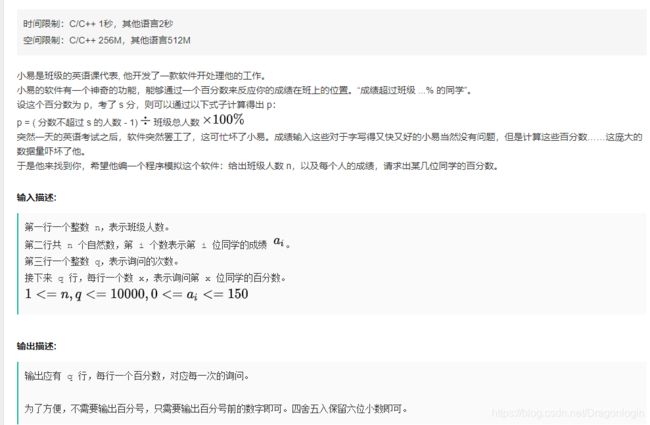
13 小易的英语软件

题面

思路

发现分数最大值是150， 题目要求每次找不超过分数x的人数，需要找10000次。

• 考虑暴力解法
  每次找不超过分数x的人数，都遍历一次数组，需要遍历10000次，肯定超时
• 优化
  优化可以优先考虑空间换时间， 所以可以用map存每个分数的人数，然后遍历分数就可以了，最多只需要遍历150次

代码

#include 
using namespace std;
const int N = 10010, M = 160;
int a[N], mp[M];
int n, q;
int main() {
    scanf("%d", &n);
    memset(mp, 0, sizeof mp);
    for (int i = 1; i <= n; ++ i) {
        scanf("%d", &a[i]);
        mp[a[i]] ++ ;
    }
    scanf("%d", &q);
    int x;
    while (q -- ) {
        scanf("%d", &x);
        int cnt = 0;
        for (int i = 0; i <= a[x]; ++ i) {
            cnt += mp[i] ;
        }
        // 必须用double，用float 错误
        double ret = (cnt - 1) * 100.0 / n ;
        printf("%.6lf\n", ret);
    }

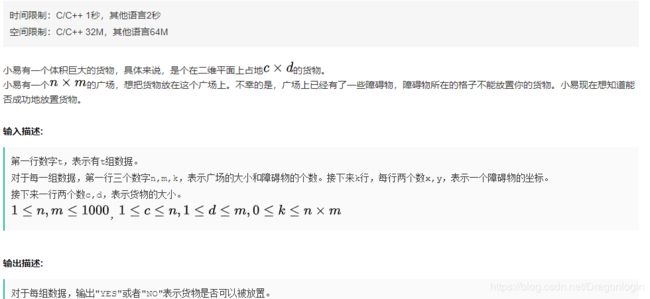
    return 0;
}

14题 放置货物

题面

思路

稍稍思考一下就会发现就是力扣85题最大矩阵和的思路。
我们可以把障碍点设为1，非障碍点设为0，跑一遍求最大0矩阵的代码，同时记录最大矩阵面积为eara，长和宽最大值maxv和最小值minv，
如果eara > c * d && maxv > max(c, d) && minv > min(c, d), 返回YES，否则NO

代码

#include 
using namespace std;
const int N = 1010;
 
int t, n, m, k, c, d;
char mat[N][N]; // 存地图，障碍物为 1 ，非障碍物为 0 

// 最大 0 矩阵面积代码模板，用数组模拟栈

int help(vector<int>& a,int &minv, int& maxv) {
    int n = a.size();
 
    int tt = 0;
    vector<int> stk(n + 10), left(n), right(n);
    // left[i] 表示左边第一个比 a[i] 值小的下标
    for (int i = 0; i < n; ++ i) {
        while (tt && a[stk[tt]] >= a[i]) tt--;
 
        if (tt) left[i] = stk[tt];
        else left[i] = -1;
 
        stk[++ tt] = i;
    }
 
    tt = 0;
    // right[i] 表示右边第一个比 a[i] 值大的下标
    for (int i = n - 1; ~i; -- i) {
        while (tt && a[stk[tt]] >= a[i]) tt--;
 
        if (tt) right[i] = stk[tt];
        else right[i] = n;
 
        stk[++ tt] = i;
    }
 
    int ret = 0;
    for (int i = 0; i < n; ++ i) {
 
        int erea = (right[i] - left[i] - 1) * a[i];
        if (ret < erea) {
            ret = erea;
            minv = min({a[i], right[i] - left[i] - 1});
            maxv = max({a[i], right[i] - left[i] - 1});
        }
    }
 
    return ret;
}
int main() {
    cin >> t;
    while (t -- ) {
        cin >> n >> m >> k;
        int x, y;
        memset(mat, 0, sizeof mat);
        for (int i = 1; i <= k ; ++i ) {
            cin >> x >> y;
            mat[x - 1][y - 1] = '1';
        }
        cin >> c >> d;
 
        vector<int> a(m + 1);
        int ret = 0;
        bool f = false;
        for (int i = 0; i < n; ++ i) {
            for (int j = 0; j < m; ++ j) {
                if (mat[i][j] == '1')
                    a[j] = 0;
                else
                    a[j] ++ ;
            }
            int minv = 0, maxv = 0;
            int ans = help(a, minv, maxv);
 
            if (ans >= c * d && minv >= (min(c, d)) && (maxv >= (max(d,c)))) {
                f = true;
                // 若满足条件，提前退出
                break;
            }
 
        }
        if (f)
            cout << "YES" <<endl;
        else
            cout << "NO" << endl;
    }
 
    return 0;
}

• 时间复杂度 O(MN)， M N为矩阵宽和长

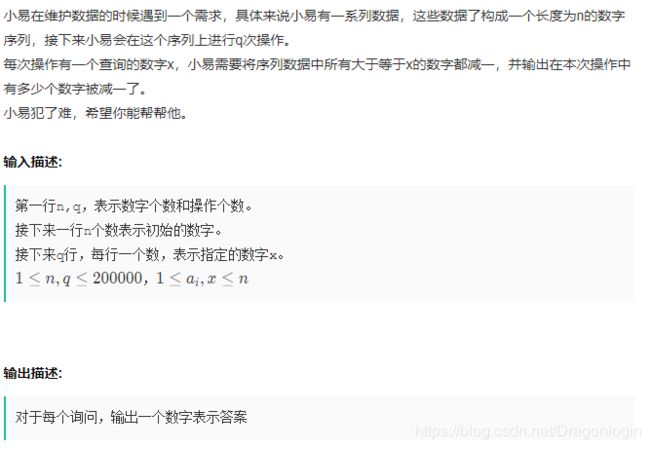
15题 序列维护

题面

思路

• 暴力解法
  暴力解法很容易想到，直接按题目说的来做就可以了
• 优化
  这个数据量，显然需要用O(nlogn)或者O(n)算法，则会想到排序，如果从大到小排，那么每次查询一个数字x，使得大于等于x的数字都会-1，那么数列还是有序的。也就是数列始终都是有序的，这样就可以进行剪枝了，遍历到小于x的直接break跳出循环即可。

代码

#include 
using namespace std;
const int N = 200010;
int a[N], hs[N];
int n, q, x;

int main() {
    scanf("%d%d", &n, &q);
    int x;
    for (int i = 1; i <= n; ++ i) {
        scanf("%d", &a[i]);
    }
    sort(a + 1, a + n + 1, greater<int>());

    while (q -- ) {
        scanf("%d", &x);
        int ret = 0;
        for (int i = 1; i <= n; ++ i) {
            if (a[i] >= x) {
                a[i] -= 1;
                ret ++ ;
            } else {
                break;
            }
        }
        printf("%d\n", ret);
    }
    return 0;
}

---

16题 按位或

题面

思路

难点就是：怎么在一个集合 a 中判断是否存在一个子集，使得子集中所有元素 或运算后的结果为 x

• 暴力想法
  找到集合a中的所有子集，然后一一判断是否满足条件。
  子集个数一共有2^n,n为集合元素个数。所以肯定超时

• 优化
  有没有可能遍历一遍集合，就可以完成。
  假设元素 x 的二进制为 100100101
  如果存在a1 | a2 | a3 | 。。。 | an = x
  根据 | 的特点，
  0 | 0 = 0,
  1 | 0 = 1,
  0 | 1 = 1,
  1 | 1 = 1
  如果我x的倒数第二位是0，那么a1, a2,…,an的倒数第二位肯定不能为1
  所以，需要满足a1 | x = x, a2 | x = x,可以用反证法证明。

代码

#include 
using namespace std;
const int N = 100010;
bool st[N];
int q, o, x;

int main() {
    scanf("%d", &q);
    vector<int> a;
    while (q --) {
        scanf("%d%d", &o, &x);
        if (o == 1) {
            if (st[x] == false)
                a.push_back(x);
                st[x] = true;
        }
        else {
            int y = 0;
            for (int v : a) {
                if ((v | x) == x)
                    y |= v;
            }

            if (y == x) {
                printf("YES\n");
            }
            else {
                printf("NO\n");
            }
        }
    }
    return 0;
}