数字图像处理——第三章 空间域图像增强（空间滤波）
文章目录
- 1. 空间滤波基础
- 2. 线性滤波器
- 2.1 平滑空间滤波器
- 2.2 锐化空间滤波器
- 2.2.1 基于一阶微分的图像增强——梯度法
- 2.2.2 基于二阶微分的图像增强——拉普拉斯算子
- 3. 非线性滤波器
- 3.1 统计排序滤波器
- 4. 总结
1. 空间滤波基础
某些邻域处理工作是操作邻域的图像像素值以及相应的与邻域有相同维数的子图像的值。这些子图像可以被称为滤波器、空间掩模、核、模板或窗口，其中前三个词是更为普遍的术语。在滤波器子图像中的值是系数值，而不是像素值。
空间滤波的机理就是在待处理图像中逐点地移动掩模，在每一点(x, y)处，滤波器在该点的响应通过事先定义的关系来计算。
对于线性空间滤波其响应由滤波器系数与滤波掩模扫过区域的相应像素值的乘积之和给出。一般来说，使用大小为mn的滤波器对大小为MN的图像进行线性空间滤波，可由下式表示：
一般来说，选取的掩模的长与宽都为奇数，其最小尺寸为3*3。当然也可以使用偶数尺寸的滤波器，或使用混合有偶数尺寸和奇数尺寸的滤波器。但是使用奇数尺寸的滤波器可以简化索引并且更为直观，因为滤波器的中心落在整数值上。
非线性空间滤波处理也是基于邻域处理，且掩模滑过一幅图像的机理与上述相同。然而，一般来说，滤波处理取决于所考虑的邻域像素点的值，而不能直接用前式中所描述的乘积求和中的系数。
2. 线性滤波器
2.1 平滑空间滤波器
平滑滤波器用于模糊处理和降低噪声。模糊处理经常用于预处理任务中，例如在（大）目标提取之前去除图像中的一些琐碎细节，以及连接直线或曲线的缝隙。通过线性滤波和非线性滤波模糊处理可以降低噪声。
平滑线性空间滤波器的输出（响应）是包含在滤波掩模邻域内像素的简单平均值。因此，这些滤波器也称为均值滤波器。 平滑滤波器用滤波掩模确定的邻域内像素的平均灰度值去代替每个像素点的值。这种处理减小了图像灰度的“尖锐”变化。由于典型的随机噪声由灰度级的尖锐变化组成，因此常见的平滑处理应用就是减噪。
由于图像边缘（几乎总是一幅图像希望有的特性）也是由图像灰度尖锐变化带来的特性，所以均值滤波处理还是存在着不希望的边缘模糊的负面效应。
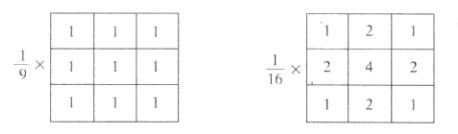
上图显示了两个3*3的平滑滤波器，第一个滤波器产生掩模下标准的像素平均值，这从把掩模系数代入前边的线性滤波公式可清楚的看出：
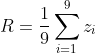
第二种掩模也叫作加权平均，使用这一术语是指不同的系数乘以像素，这样从权值上看，一些像素比另外一些更为重要。对于第二种掩模，处于掩模中心位置的像素比其他任何像素的权值都要大，因此在均值计算中给定的这一像素显得更为重要，而距离掩模中心较远的其他像素就显得不太重要了。
一幅M * N的图像经过一个m * n的加权均值滤波器的过程可由下式给出：
上述式子中，分子反映了子图像像素乘积之和。分母部分简单地表示为模板的各系数之和，它是一个仅需计算一次的常数。
下图反映了平均滤波和加权平均滤波的不同：
从上图可以看出，虽然加权平均滤波处理的要复杂许多，但是确实减小了原图像的尖锐的变化要比平均滤波小，也就是比平均滤波在边界模糊的副作用要小。
从这个图中可以更加明显的看出，加权平均滤波在边界模糊上要弱于简单平均滤波。所以在使用时就要考虑对感兴趣的物体的呈现程度，选取合适的滤波来忽略背景的影响。
工具箱使用函数imfilter来实现线性空间滤波，该函数的语法为：
在这里使用大小为3*3的简单滤波器完成实验：
>> w = ones(3)
>> imshow(f)
>> gd = imfilter(f, w)
>> figure, imshow(gd, [])
>> gr = imfilter(f, w, 'replicate')
>> figure, imshow(gr, [])
得到的结果如下图所示：
用滤波器w对图像进行卷积会产生模糊的效果，，由于滤波器是对称的，所以可以使用imfilter中默认的相关。如图，我们使用了默认边界的选项，用零填充了图像的边界，使黑白边缘模糊了。当使用参数‘replicate’后，会将亮部与边界的边缘模糊消除。
2.2 锐化空间滤波器
锐化处理的主要目的是突出图像中的细节或者增强被模糊的细节，这种模糊不是由于错误操作，就是特殊图像获取方法的固有印象。
锐化处理可以用空间微分来完成，总的来说，微分算子的响应强度与图像在该点的突变程度有关。这样一来，图像微分增强了边缘和其他突变，并削弱了灰度变化缓慢的区域。
对于一阶微分的任何定义都必须保证以下几点：
- 在平坦段微分值为零
- 在灰度阶梯或斜坡的起始点处微分值非零
- 沿着斜坡面微分值非零
因为我们处理的是数字量，其值是有限的，故最大灰度级的变化也是有限的，变化发生的最短距离是在两相邻像素之间。
对于一元函数f(x)，表达一阶微分的定义是一个差值：
这里为了与对二元图像函数f(x,y)求微分时的表达式保持一致，使用偏导数符号。对二元函数，我们将沿着两个空间轴处理偏微分。
任何二阶微分的定义也类似，也满足上述三个条件中的前二，第三个条件为沿着斜坡面微分值为零，用差分定义二阶微分：
通过比较一阶微分和二阶微分处理的响应，可以得出以下结论：
- 一阶微分处理通常会产生较宽的边缘；
- 二阶微分处理对细节有较强的响应，如细线和孤立点；
- 一阶微分处理一般对灰度阶梯有较强的响应；
- 二阶微分处理对灰度阶梯变化产生双响应，同时在图像灰度级变化相似时，二阶微分对线的响应要比对阶梯强，且点比线响应强。
2.2.1 基于一阶微分的图像增强——梯度法
在图像处理中，一阶微分是通过梯度法来实现的。对于函数f(x, y)，在其坐标(x, y)上的梯度是通过一个二维列向量来定义的：
这个向量的模值由下式给出：
尽管梯度向量的分量本身是线性算子，但这一向量的模值显然不是线性的，这是由于用到了平方和开方运算。在实际操作用，常用绝对值代替平方和开方运算。
梯度处理常用语工业检测、辅助人工检测缺陷或者更为通用的自动监测的预处理。
2.2.2 基于二阶微分的图像增强——拉普拉斯算子
首先定义一个二阶微分的离散公式，然后构造一个基于此式的滤波器，最关注的是一种各向同性滤波器，这种滤波器的响应与滤波器作用的图像的突变方向无关。
最简单的的各向同性微分算子是拉普拉斯算子，一个二元图像函数f(x, y)的拉普拉斯变换定义为：
为了更适合数字图像处理，这一方程需要表示为离散形式，由x方向和y方向的两个分量相加得到：
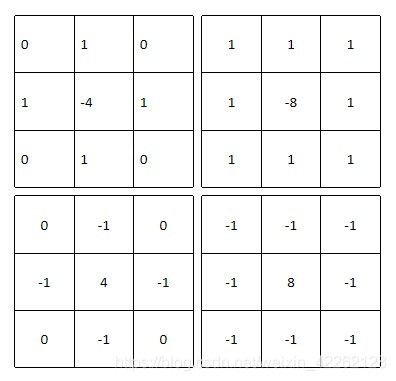
上边的公式可以由图示的掩模来实现，它们给出了以90º旋转的各向同性的结果。对角线方向也可以加入到离散拉普拉斯变换的定义中。另外两个中心为正的掩模在实践中也经常使用，这两个掩模也是以拉普拉斯变换定义为基础的，只是其中的系数与常用的符号相反。
由于拉普拉斯是一种微分算子，它的应用强调图像中灰度的突变及降低灰度慢变化的区域，这将产生一幅把图像中的浅灰色边线和突变点叠加到暗背景中的图像，将原始图像和拉普拉斯图像叠加到一起的简单方法可以保护拉普拉斯锐化处理的效果，同时又可以复原背景信息。
工具箱支持一些预定义的二维空间滤波器，这些空间滤波器可以使用函数fspecial来实现。用来生成掩模w的函数语句为：
>> w= fspecial('laplacian', 0)
w =
0 1 0
1 -4 1
0 1 0
考虑使用拉普拉斯滤波器来完成如下实验：
>> g1 = imfilter(f, w, 'replicate')
>> figure, imshow(g1, [])
>> f2 = im2double(f)
>> g2 = imfilter(f2, w, 'replicate')
>> figure, imshow(g2, [])
>> g = f2 - g2
>>figure, imshow(g)
得到的结果如下图所示：
右上角的图片显示了在应用中心为-4的掩模拉普拉斯算子后的图像，明显使图像锐化，但存在一个问题，即负值全部为0，细节的增强还不如原图像明显。之后将图片转化为double类，用原图像减去拉普拉斯运算后的结果以还原图像中失去的灰色调，即在图像锐化增强细节的同时，尽可能保留图像的灰色调。最后右下角的图可以看出，其细节的表现要比原图像更好。
3. 非线性滤波器
3.1 统计排序滤波器
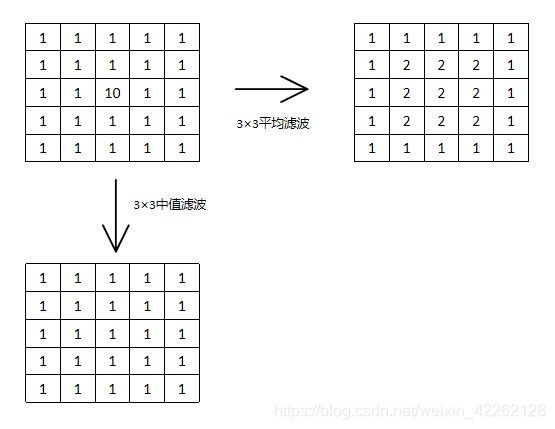
统计排序滤波器是一种非线性的空间滤波器，它的响应基于图像滤波器包围的图像区域中的像素排序，然后由统计排序结果决定的值代替中心像素的值。统计排序滤波器中最常见的例子就是中值滤波器。
中值滤波器是将像素（在中值计算中包括的原像素值）邻域内的灰度的中值代替该像素的值。 其使用非常普遍，这是因为对于一定类型的随机噪声，它提供了一种优秀的去噪能力，比小尺寸的线性平滑滤波器的模糊程度明显要低。
下图显示了平均滤波和中值滤波在处理上的不同：
从上图中可以明显看出，使用中值滤波完全消除了噪声。但是线性空间滤波是有模糊边缘效果的，可是中值滤波却不行，从下例可见：
可以看出，对于图像中特有的边缘，中值滤波却不太好处理，就需要考虑选取合适的尺寸来处理模糊细节。
4. 总结
在这一部分了解到了图像增强的另一种方法，即空间滤波。空间滤波是通过模板运算来实现的，强调像素与其周围相邻像素的关系。
主要的线性空间滤波器为平滑滤波器和锐化滤波器。平滑滤波器把每个像素都用周围的多个像素做均值操作，平滑图像速度快，算法简单。但是在降低噪声的同时，使图像产生模糊，特别是边缘和细节处，而且模糊尺寸越大，图像模糊程度就越大。空间域锐化是采用图像微分来实现的，但在增强边缘的同时，会丢失图像的层次和亮度。
非线性滤波使用模板进行计算时，结果值只取决于像素邻域的值，而非乘积和。其特点主要在于去除噪声的同时，可以较好的保护边缘的锐度和图像的细节。