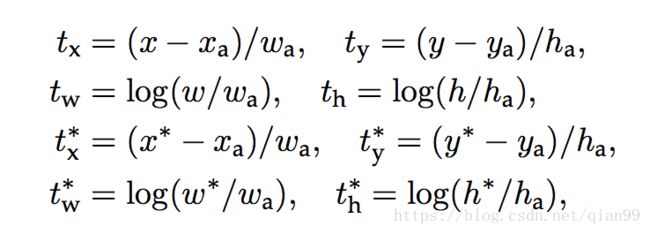FasterRcnn中boundingbox regression的一些理解

在fasterrcnn中，做框的回归，有三个输入，anchor，预测的框，groundtruth的框。一个框的表示，使用中心点 (x,y) ( x , y ) ，和框的宽高 (w,h) ( w , h ) 表示。

那么这个回归的loss怎么算呢？首先看下图：

其中：
绿框：ground truth box
红框：predict box
蓝框：anchor box

首先我们需要明白下面两个问题：
1. anchor box， ground truth box和predict box的宽高的大小之间没有大小关系，哪个框都有可能比其他框大或者小
2. 坐标值与宽高不能用绝对值，也就是用原始的坐标和宽高，这是由于做了roipooling，将每个anchorbox的feature变成了同样的size。

所以，做这个回归，要先对box的值做一些处理：

xa x a 表示anchor box的 x x , x x 表示predict box的 x x ， x∗ x ∗ 表示ground truth box的 x x 。剩下的 y,w,h y , w , h 同理。

可以看出来，这里 tx，ty t x ， t y 是计算了相对于anchor box中心点的相对距离，然后做了normalize。

但是 tw,th t w , t h 呢？为什么要用一个 log l o g 呢，刚开始一直没想明白，后来发现，这其实是个很简单的事情，上面说了，实际上的 w,h,w∗,h∗ w , h , w ∗ , h ∗ 可能大于或小于 wa,ha w a , h a ，但实际我们想要的值是一个范围是 (0,1] ( 0 , 1 ] 的值，表示预测的结果是anchor box宽高的多少倍。比较容易想到的是使用指数函数来“包装”一下：

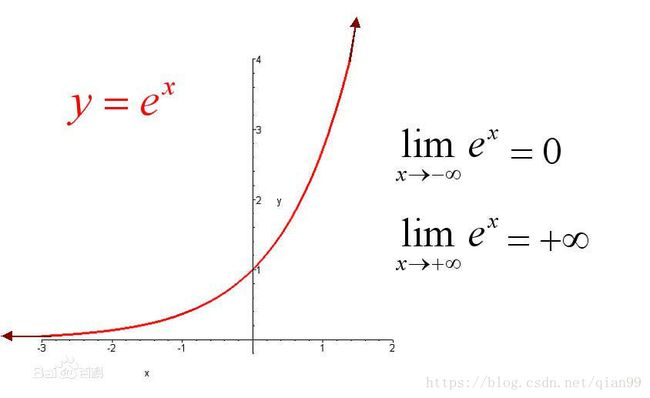
简单来说，假设回归结果为 wp,hp w p , h p ，那么实际的预测结果就应该为：

w=exp(wp)∗wa w = e x p ( w p ) ∗ w a

h=exp(hp)∗ha h = e x p ( h p ) ∗ h a

这下就清楚了，为了预测结果是exp的形式，在训练的时候，就要把输入做“反向”的处理，也就是 tw=log(w/wa) t w = l o g ( w / w a ) 。