sklearn_聚类算法K-Means

菜菜的scikit-learn课堂—sklearn中的聚类算法K-Means

1 概述

1.1 无监督学习与聚类算法

聚类算法又叫做“无监督分类”，其目的是将数据划分成有意义或有用的组（或簇）。无监督的算法在训练的时候只需要特征矩阵X，不需要标签。

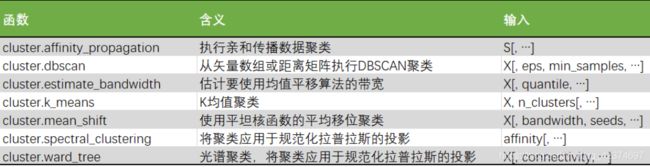
1.2 sklearn中的聚类算法

聚类算法在sklearn中有两种表现形式，

• 一种是类（和目前为止学过的分类算法以及数据预处理方法们都一样），需要实例化，训练并使用接口和属性来调用结果。

• 另一种是函数（function），只需要输入特征矩阵和超参数，即可返回聚类的结果和各种指标。

2 KMeans

2.1 KMeans是如何工作的

作为聚类算法的典型代表，KMeans可以说是最简单的聚类算法没有之一

关键概念：簇与质心
KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇，直观上来看是簇是一组一组聚集在一起的数据，在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。 簇中所有数据的均值 ${\mu }_j$ 通常被称为这个簇的“质心”（centroids）。在一个二维平面中，一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值，质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。

在KMeans算法中，簇的个数K是一个超参数，需要我们人为输入来确定。KMeans的核心任务就是根据我们设定好的K，找出K个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去。

具体过程可以总结如下：

●算法过程：
1）从N个样本数据中随机选取K个对象作为初始的聚类中心；
2）分别计算每个样本到各个聚类中心的距离，将对象分配到距离最近的聚类中；
3）所有对象分配完成后，重新计算K个聚类的中心：
4）与前一次计算得到的K个聚类中心比较，如果聚类中心发生变化，转2），否则转5）；
5）当质心不发生变化时停止并输出聚类结果。

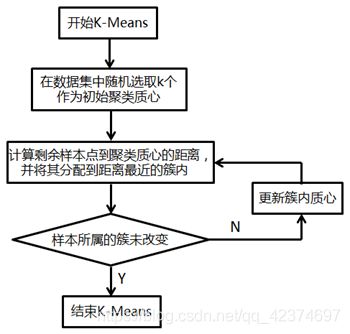
可以看见，第六次迭代之后，基本上质心的位置就不再改变了，生成的簇也变得稳定，此时聚类就完成了。

2.2 簇内误差平方和

被分在同一个簇中的数据是有相似性的，而不同簇中的数据是不同的。聚类算法的目的是追求“簇内差异小，簇外差异大”。而这个“差异“，由样本点到其所在簇的质心的距离来衡量。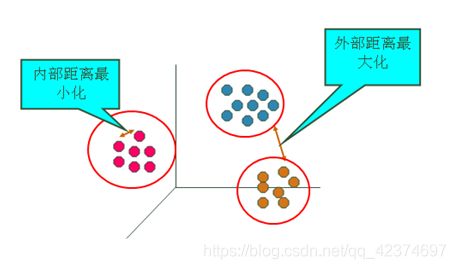

对于一个簇来说，所有样本点到质心的距离之和越小，我们就认为这个簇中的样本越相似，簇内差异就越小。而距离的衡量方法有多种，令 $x$ 表示簇中的一个样本点， $\mu$ 表示该簇中的质心，$n$ 表示每个样本点中的特征数目，$i$ 表示组成点 $x$ 的每个特征，则该样本点到质心的距离可以由以下距离来度量：

若采用欧几里得距离，则一个簇中所有样本点到质心的距离的平方和为：

其中，$m$ 为一个簇中样本的个数，$j$ 是每个样本的编号。

这个公式被称为簇内平方和（cluster Sum of Square）。而将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和（Total Cluster Sum of Square）。整体平方和越小，代表着每个簇内样本越相似，聚类的效果就越好。因此KMeans追求的是，求解能够让Inertia最小化的质心。

实际上，在质心不断变化不断迭代的过程中，总体平方和是越来越小的。我们可以使用数学来证明，当整体平方和最小的时候，质心就不再发生变化了。如此，K-Means的求解过程，就变成了一个最优化问题。

---

在KMeans中，在一个固定的簇数K下，最小化总体平方和来求解最佳质心，并基于质心的存在去进行聚类。并且，整体距离平方和的最小值其实可以使用梯度下降来求解。

Kmeans有损失函数吗？

损失函数本质是用来衡量模型的拟合效果的，只有有着求解参数需求的算法，才会有损失函数。Kmeans不求解什么参数，它的模型本质也没有在拟合数据，而是在对数据进行一
种探索。因此，K-Means不存在什么损失函数，Inertia更像是Kmeans的模型评估指标，而非损失函数。

2.3 KMeans算法的时间复杂度

使用另一种角度来度量算法：算法复杂度。

算法的复杂度分为时间复杂度和空间复杂度，时间复杂度是指执行算法所需要的计算工作量，常用大O符号表述；而空间复杂度是指执行这个算法所需要的内存空间。如果一个算法的效果很好，但需要的时间复杂度和空间复杂度都很大，那我们将会权衡算法的效果和所需的计算成本之间，

和KNN一样，KMeans算法是一个计算成本很大的算法。

在实践中，比起其他聚类算法，k-means算法已经快了，但它一般找到Inertia的局部最小值。

3 sklearn.cluster.KMeans

class  sklearn.cluster.KMeans (
			n_clusters=8, 
			init=’k-means++’, 
			n_init=10, 
			max_iter=300, 
			tol=0.0001,
			precompute_distances=’auto’, 
			verbose=0, 
			random_state=None, 
			copy_x=True, 
			n_jobs=None, 
			algorithm=’auto’)

3.1 重要参数n_clusters

n_clusters是KMeans中的 k，表示要分几类。这是KMeans当中唯一一个必填的参数，默认为8类，但通常聚类结果会是一个小于8的结果。通常，在开始聚类之前，我们并不知道n_clusters究竟是多少，因此需要对它进行探索。

使用自建数据集

from sklearn.datasets import make_blobs 
import matplotlib.pyplot as plt

#自己创建数据集 
X, y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)

X.shape # (500, 2)
y.shape

fig, ax1 = plt.subplots(1) 
ax1.scatter(X[:, 0], X[:, 1]#.scatter散点图 
            ,marker='o' #点的形状 
            ,s=8 #点的大小 
           ) 
plt.show()

#如果我们想要看见这个点的分布，怎么办？
color = ["red","pink","orange","gray"]
fig, ax1 = plt.subplots(1)

for i in range(4):
    ax1.scatter(X[y==i, 0], X[y==i, 1]
            ,marker='o' #点的形状
            ,s=8 #点的大小
            ,c=color[i]
           )
plt.show()

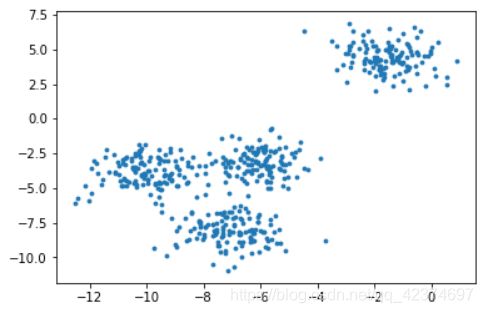
基于这个分布，我们来使用Kmeans进行聚类。首先，我们要猜测一下，这个数据中有几簇？

from sklearn.cluster import KMeans
n_clusters = 3  # 先猜测 k=3
cluster = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
#重要属性Labels_，查看聚好的类别，每个样本所对应的类
y_pred = cluster.labels_
y_predd
'''
array([0, 0, 2, 1, 2, 1, 2, 2, 2, 2, 0, 0, 2, 1, 2, 0, 2, 0, 1, 2, 2, 2,
       2, 1, 2, 2, 1, 1, 2, 2, 0, 1, 2, 0, 2, 0, 2, 2, 0, 2, 2, 2, 1, 2,
       ....
'''

#KMeans因为并不需要建立模型或者预测结果，因此我们只需要fit就能够得到聚类结果了
#KMeans也有接口predict和fit_predict，表示学习数据X并对X的类进行预测
#但所得到的结果和我们不调用predict，直接fit之后调用属性labels一模一伴
pre = cluster.fit_predict(X)
pre
'''
array([0, 0, 2, 1, 2, 1, 2, 2, 2, 2, 0, 0, 2, 1, 2, 0, 2, 0, 1, 2, 2, 2,
       2, 1, 2, 2, 1, 1, 2, 2, 0, 1, 2, 0, 2, 0, 2, 2, 0, 2, 2, 2, 1, 2,
       ....
'''

什么时候需要predict呢？当数据量太大的时候！

其实我们不必使用所有的数据来寻找质心，少量的数据就可以帮助我们确定质心了，

当数据量非常大的时候，可以使用部分数据来帮助我们确认质心，剩下的数据的聚类结果，使用predict来调用

cluster_smallsub = KMeans(n_clusters=n_clusters, random_state=0).fit(X[:200])
y_pred_ = cluster_smallsub.predict(X)
'''
array([1, 1, 2, 0, 2, 0, 2, 2, 2, 2, 1, 1, 2, 0, 2, 1, 2, 1, 0, 2, 2, 2,
       2, 0, 2, 2, 0, 0, 2, 2, 1, 0, 2, 1, 2, 1, 2, 2, 1, 2, 2, 2, 0, 2,
'''
y_pred == y_pred_#数据量非常大的时候，效果会好
'''
array([False, False,  True, False,  True, False,  True,  True,  True,
        True, False, False,  True, False,  True, False,  True, False,
'''
#但从运行得出这样的结果，肯定与直接fit全部数据会不一致。有时候，当不要求那么精确，或者我们的数据量实在太大，那我们可以使用这种方法，使用接口predict
#如果数据量还行，不是特别大，直接使用fit之后调用属性.labels_提出来

#重要属性cLuster_centers_，查看质心
centroid = cluster.cluster_centers_
centroid
'''
array([[-7.09306648, -8.10994454],
       [-1.54234022,  4.43517599],
       [-8.0862351 , -3.5179868 ]])
'''
centroid.shape # (3, 2)


#重要属性inertia_，查看总距离平方和
inertia = cluster.inertia_
inertia
# 1903.4503741659223

color = ["red","pink","orange","gray"]

fig, ax1 = plt.subplots(1)

for i in range(n_clusters):
    ax1.scatter(X[y_pred==i, 0], X[y_pred==i, 1]
            ,marker='o' #点的形状
            ,s=8 #点的大小
            ,c=color[i]
           )
# 质心    
ax1.scatter(centroid[:,0],centroid[:,1]
           ,marker="x"
           ,s=15
           ,c="black")
plt.show()

n_clusters = 4  # 猜测 k=4
cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
inertia_ = cluster_.inertia_
inertia_
# 908.3855684760613

n_clusters = 5
cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
inertia_ = cluster_.inertia_
inertia_
# 811.0841324482415

n_clusters = 6
cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)
inertia_ = cluster_.inertia_
inertia_
# 733.153835008308

随着 n_clusters 越来越大，inertia 可以变成0

我们不能够通过调节 n_clusters ，降低 inertia ，来表示模型效果变好了，模型的效果变好只有在 n_clusters 固定的时候。

3.1.1 聚类算法的模型评估指标

不同于分类模型和回归，聚类算法的模型评估不是一件简单的事。在分类中，有直接结果（标签）的输出，并且分类的结果有正误之分，所以我们使用预测的准确度，混淆矩阵，ROC曲线等等指标来进行评估，但无论如何评估，都是在”模型找到正确答案“的能力。而回归中，由于要拟合数据，我们有SSE均方误差，有损失函数来衡量模型的拟合程度。但这些衡量指标都不能够使用于聚类。

如何衡量聚类算法的效果？

KMeans的目标是确保“簇内差异小，簇外差异大”，可以通过衡量簇内差异来衡量聚类的效果。而Inertia是用距离来衡量簇内差异的指标，因此，是否可以使用Inertia来作为聚类的衡量指标呢？。

可以，但是这个指标的缺点和极限太大。

• 第一，它不是有界的。我们只知道，Inertia是越小越好，是0最好，但我们不知道，一个较小的Inertia究竟有没有达到模型的极限，能否继续提高。

• 第二，它的计算太容易受到特征数目的影响，数据维度很大的时候，Inertia的计算量会陷入维度诅咒之中，计算量会爆炸，不适合用来一次次评估模型。

• 第三，它会受到超参数K的影响，在我们之前的常识中其实我们已经发现，随着K越大，Inertia注定会越来越小，但这并不代表模型的效果越来越好了。

• 第四，Inertia对数据的分布有假设，它假设数据满足凸分布（即数据在二维平面图像上看起来是一个凸函数的样子），并且它假设数据是各向同性的（isotropic），即是说数据的属性在不同方向上代表着相同的含义。但是现实中的数据往往不是这样。

所以使用Inertia作为评估指标，会让聚类算法在一些细长簇，环形簇，或者不规则形状的
流形时表现不佳：

事实上，K-Means更擅长一堆一堆分开的数据

3.1.1.1 当真实标签已知的时候

虽然在聚类中不输入真实标签，但这不代表数据中一定不具有真实标签，或者一定没有任何参考信息。

当然，在现实中，拥有真实标签的情况非常少见（几乎是不可能的）。如果拥有真实标签，更倾向于使用分类算法。但不排除我们依然可能使用聚类算法的可能性。如果有样本真实聚类情况的数据，可以对于聚类算法的结果和真实结果来衡量聚类的效果。

3.1.1.2 当真实标签未知的时候：轮廓系数

大部分情况下，是对没有真实标签的数据进行探索，也就是对不知道真正答案的数据进行聚类。这样的聚类，是完全依赖于评价簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来评估聚类的效果。

其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的，它能够同时衡量：

1）样本与其自身所在的簇中的其他样本的相似度a，等于样本与同一簇中所有其他点之间的平均距离

2）样本与其他簇中的样本的相似度b，等于样本与下一个最近的簇中的所有点之间的平均距离

根据聚类的要求”簇内差异小，簇外差异大“，我们希望b永远大于a，并且大得越多越好。
单个样本的轮廓系数计算为：

$$s=\frac{b-a}{\max \left(a,b\right)}$$

公式可以被解析为：
$$s=\{\begin{array}{l}1-a/b\text{，}ifa<b\\ \\ 0\text{，}ifa=b\\ \\ b/a-1\text{，}ifa>b\end{array}$$

很容易理解轮廓系数范围是(-1,1)，其中值越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似，当样本点与簇外的样本更相似的时候，轮廓系数就为负。当轮廓系数为0时，则代表两个簇中的样本相似度一致，两个簇本应该是一个簇。

可以总结为轮廓系数越接近于1越好，负数则表示聚类效果非常差。

如果一个簇中的大多数样本具有比较高的轮廓系数，则簇会有较高的总轮廓系数，则整个数据集的平均轮廓系数越高，则聚类是合适的。如果许多样本点具有低轮廓系数甚至负值，则聚类是不合适的，聚类的超参数K可能设定得太大或者太小。

---

在sklearn中，使用模块metrics中的类silhouette_score来计算轮廓系数，它返回的是一个数据集中所有样本的轮廓系数的均值。

metrics模块中的silhouette_sample，它的参数与轮廓系数一致，但返回的是数据集中每个样本自己的轮廓系数。

我们来看看轮廓系数在我们自建的数据集上表现如何：

from sklearn.metrics import silhouette_score
from sklearn.metrics import silhouette_samples
X.shape#(500, 2)
y_pred #.labels_  3簇
'''
array([0, 0, 2, 1, 2, 1, 2, 2, 2, 2, 0, 0, 2, 1, 2, 0, 2, 0, 1, 2, 2, 2,
       2, 1, 2, 2, 1, 1, 2, 2, 0, 1, 2, 0, 2, 0, 2, 2, 0, 2, 2, 2, 1, 2,
'''

返回的是一个数据集中所有样本的轮廓系数的均值

silhouette_score(X,y_pred)
0.5882004012129721

silhouette_score(X,cluster_.labels_) #分4簇的确比分3簇效果要好
0.6505186632729437

silhouette_score(X,cluster_.labels_) #分5簇
0.5746932321727456

silhouette_score(X,cluster_.labels_) #分6簇
0.5150064498560357

分4簇，轮廓系数最高

---

返回的是数据集中每个样本自己的轮廓系数

silhouette_samples(X,y_pred)
'''
array([ 0. 62982017,0.5034877,0.56148795, 0. 84881844,0.56034142,
		0.78740319,0.39254042, 0.4424015 ,0. 48582704,0. 41586457,
		.....
'''

silhouette_samples(X,y_pred).shape#(500,)
silhouette_samples(X,y_pred).mean() # 0.5882004012129721

轮廓系数有很多优点，它在有限空间中取值，使得我们对模型的聚类效果有一个“参考”。并且，轮廓系数对数据的分布没有假设，因此在很多数据集上都表现良好。但它在每个簇的分割比较清洗时表现最好。

但轮廓系数也有缺陷，它在凸型的类上表现会虚高，比如基于密度进行的聚类，或通过DBSCAN获得的聚类结果，如果使用轮廓系数来衡量，则会表现出比真实聚类效果更高的分数。

3.1.1.3 当真实标签未知的时候：Calinski-Harabaz Index

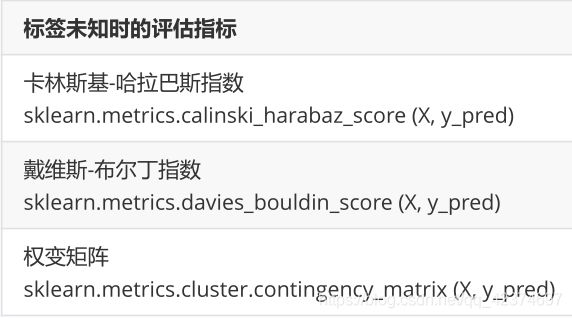
除了轮廓系数是最常用的，还可以使用

• 卡林斯基-哈拉巴斯指数（Calinski-Harabaz Index，简称CHI，也被称为方差比标准）
• 戴维斯-布尔丁指数（Davies-Bouldin）
• 权变矩阵（Contingency Matrix）

卡林斯基-哈拉巴斯指数越高越好。对于有k个簇的聚类而言，卡林斯基-哈拉巴斯指数s(k)写作如下公式：

from sklearn.metrics import calinski_harabaz_score

X
y_pred

calinski_harabaz_score(X, y_pred)
1809. 991966958033

虽然calinski-Harabaz指数没有界，在凸型的数据上的聚类也会表现虚高。但是比起轮廓系数，它有一个巨大的优点，就是计算非常快速。

3.1.3 案例：基于轮廓系数来选择n_clusters

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm #colormap
import numpy as np
import pandas as pd

#先设定我们要分成的簇数
n_clusters = 4

#创建--个画布，画布上共有一行两列两个图
fig, (ax1, ax2) = plt.subplots(1, 2)

#画布尺寸
fig.set_size_inches(18,7)

#第一个图是轮廓系数图像，是由各个簇的轮廓系数组成的横向条形图
#横向条形图的横坐标是轮廓系数取值。纵坐标是每个样本，因为轮廓系数是对于每一-个样本进行计算的


#首先我们来设定横坐标
#轮廓系数的取值范围在[-1，1]之间，但我们希望轮廓系数至少是要大0的
#太长的横坐标不利于可视化，所以只设定X轴的取值在[-0.1，1]之间
ax1.set_xlim([-0.1, 1])


#接下来设定纵坐标，通常来说，纵坐标是从0开始，最大值取到X.shape[0]的取值
#但我们希望，每个簇能够排在一起，不同的簇之间能够有一-定的空隙
#以便我们看到不同的条形图聚合成的块，理解它是对应了哪一个簇
#因此我们在设定纵坐标的取值范围的时候，在X.shape[0]上，加上--个距离（n_clusters + 1）*10，留作间隔用
ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])

# 开始建模
clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)

#重要属性Labels_，查看聚好的类别，每个样本所对应的类
cluster_labels = clusterer.labels_

#调用轮廓系数分数，注意，silhouette_score 生成的是所有样本点的轮廓系数均值
#两个需要输入的参数是，特征矩阵X和聚类完毕后的标签
silhouette_avg = silhouette_score(X, cluster_labels)

#现在的簇数量（n_clusters）下，整体的轮廓系数究竟有多少
print("For n_clusters =", n_clusters,
      "The average silhouette_score is :", silhouette_avg)

#调用silhouette_samples，返回每个样本点的轮廓系数，这就是我们的横坐标
sample_silhouette_values = silhouette_samples(X, cluster_labels)

#设定y轴上的初始取值，使与X轴有一定的距离
y_lower = 10

# 对每一簇进行循环
for i in range(n_clusters):
    #从每个样本的轮廓系数结果中抽取出第i个簇的轮廓系数，并对他进行排序
    ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
    
    #注意，.sort（）这 个命令会直接改掉原数据的顺序
    ith_cluster_silhouette_values.sort()
    
    #查看这一个簇中究竞有多少个样本
    size_cluster_i = ith_cluster_silhouette_values.shape[0]
    
    #colormap库中的，使用小数来调用颜色的丽数
    #在nipy_spectral（[输入任意小数来代表一个颜色]）
    #在这里我们希望每个颜的颜色是不同的，我们需要的颜色种类刚好是循环的个数的种类
    #在这里，只要能够确保，每次循环生成的小数是不同的，可以使用任意 方式来获取小数
    #在这里，我是用的浮点数除以n_clusters，在不同的下，自然生成不同的小数
    #以确保所有的簇会有不同的颜色
    y_upper = y_lower + size_cluster_i
    color = cm.nipy_spectral(float(i)/n_clusters)
    
    
    #开始填充子图81中的内容
    #fill_between是让--个范围中的柱状图都统--颜色的函数
    #fill_betweenx的范围是在纵坐标上#fill_betweeny的范围是在横坐标上
    #fill_betweenx的参 数应该输入（纵坐标的下限，纵坐标的上限，柱状图的颜色）
    ax1.fill_betweenx(np.arange(y_lower, y_upper)
                      ,ith_cluster_silhouette_values
                      ,facecolor=color
                      ,alpha=0.7
                     )

    #为每个簇的轮廓系数写上簇的编号，并且让簇的编号显示坐标轴上每个条形图的中间位置'
    #text的参数为（要显示编号的位置的横坐标，要显示编号的位置的纵坐标，要显示的编号内容）
    ax1.text(-0.05
             , y_lower + 0.5 * size_cluster_i
             , str(i))
    #为下一个簇计算新的y轴上的初始值，是每一次迭代之后，y的上线再加上10
    #以此来保证，不同的簇的图像之间显示有空隙
    y_lower = y_upper + 10

#给图1加上标题，横坐标轴，纵座标轴的标签
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")

#把整个数据集上的轮廓系数的均值以虚线的形式放入我们的图中
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

#y轴不显示任何刻度
ax1.set_yticks([])
#x轴上的刻度显示为我们规定的列表
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

#开始对第二个图进行处理，首先获取新颜色，由于这里没有循环，因此我们需要一次性生成多个小数来获取多个颜色
# cluster_labels.astype(float)就是把0,1,2,3变为浮点数，相同的浮点数有相同的颜色
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)

ax2.scatter(X[:, 0], X[:, 1]
            ,marker='o'
            ,s=8
            ,c=colors
           )
#把生成的质心放到图像中去
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='x',
            c="red", alpha=1, s=200)

ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")

plt.suptitle(("Silhouette analysis for KMeans clustering on sample data"
              "with n_clusters = %d" % n_clusters),
             fontsize=14, fontweight='bold')
plt.show()

可见，蓝色的所有样本的轮廓系数都过平均线，说明蓝色的簇分的最好，剩下的簇，都有一半或者三分之一的样本的轮廓系数过平均线，基本上分簇较好

将上述过程包装成一个循环，可以得到：

n_clusters 分别等于2，3，4，5，6，7，查看每一种聚类的最终效果

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score

import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np

for n_clusters in [2,3,4,5,6,7]:
    n_clusters = n_clusters
    fig, (ax1, ax2) = plt.subplots(1, 2)
    fig.set_size_inches(18, 7)
    ax1.set_xlim([-0.1, 1])
    ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])
    clusterer = KMeans(n_clusters=n_clusters, random_state=10).fit(X)
    cluster_labels = clusterer.labels_
    silhouette_avg = silhouette_score(X, cluster_labels)
    print("For n_clusters =", n_clusters,
          "The average silhouette_score is :", silhouette_avg)
    sample_silhouette_values = silhouette_samples(X, cluster_labels)
    y_lower = 10
    for i in range(n_clusters):
        ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
        ith_cluster_silhouette_values.sort()
        size_cluster_i = ith_cluster_silhouette_values.shape[0]
        y_upper = y_lower + size_cluster_i
        color = cm.nipy_spectral(float(i)/n_clusters)
        ax1.fill_betweenx(np.arange(y_lower, y_upper)
                          ,ith_cluster_silhouette_values
                          ,facecolor=color
                          ,alpha=0.7
                         )
        ax1.text(-0.05
                 , y_lower + 0.5 * size_cluster_i
                 , str(i))
        y_lower = y_upper + 10

    ax1.set_title("The silhouette plot for the various clusters.")
    ax1.set_xlabel("The silhouette coefficient values")
    ax1.set_ylabel("Cluster label")
    ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
    ax1.set_yticks([])
    ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])

    colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
    ax2.scatter(X[:, 0], X[:, 1]
                ,marker='o'
                ,s=8
                ,c=colors
               )
    centers = clusterer.cluster_centers_
    # Draw white circles at cluster centers
    ax2.scatter(centers[:, 0], centers[:, 1], marker='x',
                c="red", alpha=1, s=200)
    
    ax2.set_title("The visualization of the clustered data.")
    ax2.set_xlabel("Feature space for the 1st feature")
    ax2.set_ylabel("Feature space for the 2nd feature")

    plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
                  "with n_clusters = %d" % n_clusters),
                 fontsize=14, fontweight='bold')
    plt.show()

当聚为2类时
For n_clusters = 2 The average silhouette_score is : 0.7049787496083262

当聚为3类时
For n_clusters = 3 The average silhouette_score is : 0.5882004012129721

当聚为4类时
For n_clusters = 4 The average silhouette_score is : 0.6505186632729437

当聚为5类时
For n_clusters = 5 The average silhouette_score is : 0.56376469026194

当聚为6类时
For n_clusters = 6 The average silhouette_score is : 0.4504666294372765

当聚为7类时
For n_clusters = 7 The average silhouette_score is : 0.39092211029930857

具体是聚2类还是4类，需要结合业务需求而定

3.2 重要参数init & random_state & n_init

初始质心怎么放好?

在K-Means中有一个重要的环节，就是放置初始质心。如果有足够的时间，K-means一定会收敛，但Inertia可能收敛到局部最小值。是否能够收敛到真正的最小值很大程度上取决于质心的初始化。

init 就是用来帮助我们决定初始化方式的参数。

初始质心放置的位置不同，聚类的结果很可能也会不一样，一个好的质心选择可以让K-Means避免更多的计算，让算法收敛稳定且更快。

使用”随机“的方法在样本点中抽取k个样本作为初始质心，这种方法显然不符合”稳定且更快“的需求。为此，我们可以使用random_state参数来控制每次生成的初始质心都在相同位置。

一个random_state对应一个质心随机初始化的随机数种子。如果不指定随机数种子，则sklearn中的K-means并不会只选择一个随机模式扔出结果，而会在每个随机数种子下运行多次，并使用结果最好的一个随机数种子来作为初始质心。我们可以使用参数 n_init 来选择，每个随机数种子下运行的次数。这个参数不常用到，默认10次，

如果希望运行的结果更加精确，那可以增加这个参数 n_init 的值来增加每个随机数种子下运行的次数。

为了优化选择初始质心的方法，**开发了”k-means ++“初始化方案，使得初始质心（通常）彼此远离，以此来引导出比随机初始化更可靠的结果。在sklearn中，使用参数init ='k-means ++'来选择使用k-means ++作为质心初始化的方案（默认）。

参数	说明
init	可输入"k-means++"，“random"或者一个n维数组。 这是初始化质心的方法，默认"k-means++”。 输入"k-means++"：一种为K均值聚类选择初始聚类中心的聪明的办法，以加速收敛。如果输入了n维数组，数组的形状应该是(n_clusters，n_features)并给出初始质心。
random_state	控制每次质心随机初始化的随机数种子
n_init	整数，默认10，使用不同的质心随机初始化的种子来运行k-means算法的次数。最终结果会是基于Inertia来计算的n_init次连续运行后的最佳输出

3.3 重要参数max_iter & tol

让迭代停下来

在之前提到过，当质心不再移动，Kmeans算法就会停下来。但在完全收敛之前，也可以使用max_iter，最大迭代次数，或者tol，两次迭代间Inertia下降的量，这两个参数来让迭代提前停下来。

有时候，当n_clusters选择不符合数据的自然分布，或者为了业务需求，必须要填入与数据的自然分布不合的n_clusters，提前让迭代停下来反而能够提升模型的表现。

参数	说明
max_iter	整数，默认300，单次运行的k-means算法的最大迭代次数
tol	浮点数，默认1e-4，两次迭代间Inertia下降的量，如果两次迭代之间Inertia下降的值小于tol所设定的值，迭代就会停下

random = KMeans(n_clusters = 10,init="random",max_iter=10,random_state=420).fit(X)
y_pred_max10 = random.labels_
silhouette_score(X,y_pred_max10)
0.3952586444034157

random = KMeans(n_clusters = 10,init="random",max_iter=20,random_state=420).fit(X)
y_pred_max20 = random.labels_
silhouette_score(X,y_pred_max20)
0.3401504537571701

3.4 重要属性与重要接口

3.5 函数cluster.k_means

sklearn.cluster.k_means (X, n_clusters, sample_weight=None, init=’k-means++’, precompute_distances=’auto’,
n_init=10, max_iter=300, verbose=False, tol=0.0001, random_state=None, copy_x=True, n_jobs=None,
algorithm=’auto’, return_n_iter=False)

函数k_means的用法其实和类非常相似，不过函数是输入一系列值，而直接返回结果。一次性地，函数k_means会依次返回质心，每个样本对应的簇的标签，inertia以及最佳迭代次数。

from sklearn.cluster import k_means

k_means(X,4,return_n_iter=False)

'''
(array([[ -6.08459039,  -3.17305983],
        [ -1.54234022,   4.43517599],
        [ -7.09306648,  -8.10994454],
        [-10.00969056,  -3.84944007]]),
 array([2, 2, 3, 1, 0, 1, 0, 0, 0, 0, 2, 2, 0, 1, 0, 2, 0, 2, 1, 0, 3, 3,
        0, 1, 0, 0, 1, 1, 3, 0, 2, 1, 0, 2, 0, 2, 3, 3, 2, 3, 0, 3, 1, 0,
        0, 2, 3, 0, 1, 1, 1, 3, 3, 0, 2, 3, 3, 3, 3, 0, 1, 1, 3, 0, 1, 0,
        2, 0, 3, 3, 2, 3, 0, 2, 0, 0, 2, 0, 0, 3, 1, 1, 3, 1, 1, 3, 3, 1,
        3, 3, 1, 2, 3, 0, 1, 2, 2, 0, 2, 1, 1, 2, 1, 3, 1, 0, 0, 1, 1, 3,
        0, 2, 1, 3, 1, 3, 1, 0, 1, 0, 3, 2, 2, 3, 0, 3, 1, 2, 2, 0, 1, 3,
        3, 3, 3, 2, 1, 0, 1, 1, 0, 2, 0, 1, 1, 1, 0, 0, 2, 2, 3, 3, 1, 2,
        1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 1, 2, 2, 2, 0, 1, 2, 3, 0, 2, 1, 3,
        3, 3, 3, 2, 0, 3, 1, 2, 2, 3, 0, 2, 2, 0, 1, 1, 2, 2, 0, 1, 0, 2,
        2, 1, 2, 3, 1, 0, 0, 2, 0, 3, 2, 0, 3, 0, 3, 2, 0, 0, 0, 1, 3, 1,
        0, 2, 3, 0, 3, 3, 3, 1, 3, 1, 2, 3, 2, 3, 1, 1, 3, 2, 1, 2, 0, 3,
        2, 2, 2, 2, 0, 3, 2, 3, 0, 1, 1, 0, 0, 1, 3, 0, 3, 1, 0, 1, 3, 3,
        1, 0, 2, 2, 3, 3, 3, 0, 1, 1, 0, 1, 3, 2, 1, 2, 1, 2, 2, 1, 2, 1,
        1, 0, 3, 3, 3, 0, 0, 3, 2, 1, 2, 2, 2, 0, 3, 0, 2, 3, 2, 2, 3, 2,
        2, 3, 1, 2, 0, 0, 1, 1, 3, 2, 1, 1, 0, 2, 1, 1, 0, 3, 1, 3, 0, 2,
        2, 1, 3, 2, 0, 1, 1, 0, 0, 0, 2, 0, 1, 1, 3, 1, 1, 1, 1, 2, 2, 0,
        1, 3, 0, 2, 1, 3, 1, 0, 1, 3, 0, 3, 1, 0, 0, 2, 1, 2, 2, 2, 2, 2,
        2, 3, 2, 1, 2, 1, 1, 3, 1, 0, 3, 3, 2, 1, 3, 1, 0, 2, 3, 3, 2, 3,
        3, 1, 1, 2, 3, 0, 1, 0, 0, 2, 2, 0, 2, 3, 3, 2, 3, 2, 3, 1, 2, 1,
        3, 0, 1, 3, 0, 1, 2, 0, 1, 1, 3, 0, 3, 0, 2, 1, 2, 0, 1, 2, 2, 2,
        3, 1, 0, 2, 0, 0, 3, 3, 2, 0, 0, 0, 0, 0, 0, 2, 0, 3, 2, 0, 1, 0,
        1, 0, 3, 3, 1, 1, 1, 3, 0, 3, 2, 3, 1, 0, 2, 1, 2, 1, 2, 0, 1, 1,
        2, 3, 0, 2, 3, 3, 3, 2, 0, 1, 3, 0, 2, 2, 2, 0]),
 908.3855684760613)
'''