牛客编程巅峰赛S1第5场 题解
完全平方数的尾巴
思路:暴力枚举。
考虑 a 2 ( m o d p ) = a ( m o d p ) × a ( m o d p ) a^2\pmod p=a\pmod p \times a\pmod p a2(modp)=a(modp)×a(modp)。
所以当 a = 1000 a=1000 a=1000时又回到 a = 0 a=0 a=0,即周期为 T = 1000 T=1000 T=1000。
所以我们只需要暴力枚举 a ∈ [ 0 , 999 ] a\in[0,999] a∈[0,999]特判 a 2 ( m o d 1000 ) = x a^2\pmod {1000}=x a2(mod1000)=x。
时间复杂度: O ( n ) O(n) O(n)
typedef long long ll;
class Solution {
public:
/**
*
* @param x int整型
* @return bool布尔型
*/
bool solve(int x) {
for(int i=0;i<1000;i++)
if(i*i%1000==x) return true;
return false;
}
};
牛牛的字符串
思路:归并排序
此题的实质就是求序列的逆序对数,使得整个字符串呈非递增序列。
因为此题字符集只有 ∣ Σ ∣ = 26 |\Sigma|=26 ∣Σ∣=26。所以我们可以考虑用 d p dp dp实现。
令 d p [ i ] [ j ] dp[i][j] dp[i][j]表示前 i i i个集合中,字符 j + ′ a ′ j+'a' j+′a′的个数。
显然每次我们只需统计对 k k k取模后,比当前字符 s [ i ] s[i] s[i]小的字符个数即可。
即: ∑ j < s [ i ] − ′ a ′ d p [ i % k ] [ j ] \sum\limits_{j
时间复杂度: O ( 26 n ) O(26n) O(26n)。
class Solution {
public:
int turn(string s, int k) {
int n=s.size(),ans=0;
vector<vector<int> >dp(k,vector<int>(26,0));
for(int i=0;i<n;i++){
for(int j=0;j<s[i]-'a';j++) ans+=dp[i%k][j];
dp[i%k][s[i]-'a']++;
}
return ans;
}
};
另外此题还可以用树状数组和线段树写,用权值树状数组维护一下前缀和即可。
时间复杂度: O ( n l o g 26 ) O(nlog26) O(nlog26)
#define lowbit(x) x&(-x)
const int N=1e5+5;
class Solution {
public:
int tr[N][30],sz=26;
void upd(int p,int x,int k){
while(x<=26){
tr[p][x]+=k;
x+=lowbit(x);
}
}
int query(int p,int x){
int ans=0;
while(x){
ans+=tr[p][x];
x-=lowbit(x);
}
return ans;
}
int turn(string s, int k) {
memset(tr,0,sizeof tr);
int n=s.size();
int ans=0;
for(int i=0;i<n;i++){
int p=i%k;
ans+=query(p,s[i]-'a');
upd(p,s[i]-'a'+1,1);
}
return ans;
}
};
下棋
思路:二维前缀和。
考虑:每次增加的贡献是多少,显然是一个类似于两个矩阵重合的图形。
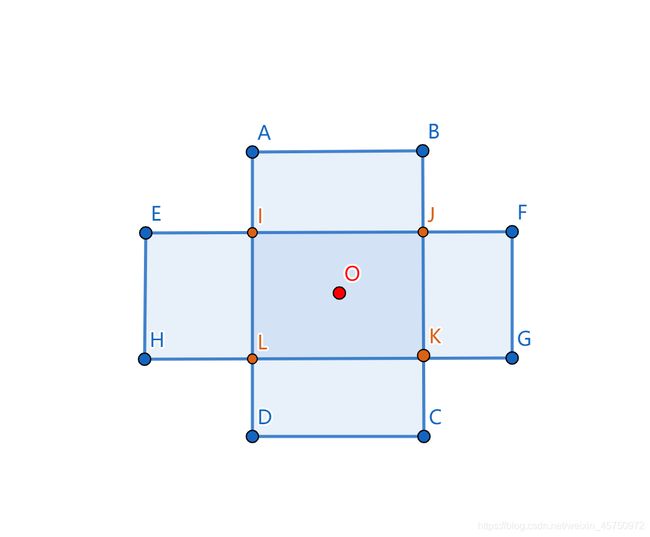
对于当前点: O ( x , y ) O(x,y) O(x,y),因为是在 s t e p step step范围内。
对应矩阵的几个边界点:
A ( 1 , y − s t e p + 1 ) , C ( n , y + s t e p − 1 ) → 矩 形 A B C D A(1,y-step+1),C(n,y+step-1)\rightarrow 矩形ABCD A(1,y−step+1),C(n,y+step−1)→矩形ABCD
E ( x − s t e p + 1 , 1 ) , G ( x + s t e p − 1 , n ) → 矩 形 E F G H E(x-step+1,1),G(x+step-1,n)\rightarrow 矩形EFGH E(x−step+1,1),G(x+step−1,n)→矩形EFGH
I ( x − s t e p + 1 , y − s t e p + 1 ) , K ( x + s t e p − 1 , y + s t e p − 1 ) → 矩 形 I J K L I(x-step+1,y-step+1),K(x+step-1,y+step-1)\rightarrow 矩形IJKL I(x−step+1,y−step+1),K(x+step−1,y+step−1)→矩形IJKL
所以该图形的贡献是: S A B C D + S E F G H − S I J K L S_{ABCD}+S_{EFGH}-S_{IJKL} SABCD+SEFGH−SIJKL
所以我们只需要维护一下二维前缀和即可算出答案,需要注意的是边界情况。
时间复杂度: O ( n 2 + q ) O(n^2+q) O(n2+q)
const int N=2e3+10;
typedef long long ll;
class Solution {
public:
ll pre[N][N],a[N][N],mod=1e9+7;
int d[4][2]={0,1,1,0,0,-1,-1,0};
struct P{
int x,y;
}b[N*N];
ll cal(int n,int x1,int y1,int x2,int y2){
if(x1<1) x1=1;if(y1<1) y1=1;
if(x2>n) x2=n;if(y2>n) y2=n;
return pre[x2][y2]-pre[x2][y1-1]-pre[x1-1][y2]+pre[x1-1][y1-1];
}
vector<int> getScores(int n, vector<int>& query) {
int x=1,y=1,id=0;
for(int i=1;i<=n*n;i++){
a[x][y]=i;b[i]={x,y};
int nx=x+d[id][0],ny=y+d[id][1];
if(a[nx][ny]||nx<1||nx>n||ny<1||ny>n) id=(id+1)%4;
x+=d[id][0],y+=d[id][1];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];
//printf("pre[%d][%d]=%d\n",i,j,pre[i][j]);
}
vector<int>ans;
ll sum=0;
int pos=1;
for(int i=0;i<query.size();i++){
int step=query[i];
pos=(pos+step-1)%(n*n)+1;
int x=b[pos].x,y=b[pos].y;
sum+=cal(n,x-step+1,1,x+step-1,n)+cal(n,1,y-step+1,n,y+step-1);
sum-=cal(n,x-step+1,y-step+1,x+step-1,y+step-1);
sum%=mod;
ans.push_back((int)sum);
}
return ans;
}
};