GraphX入门简介

GraphX入门

1.     GraphX应用背景

   Spark GraphX是一个分布式图处理框架，它是基于Spark平台提供对图计算和图挖掘简洁易用的而丰富的接口，极大的方便了对分布式图处理的需求。

众所周知·，社交网络中人与人之间有很多关系链，例如Twitter、Facebook、微博和微信等，这些都是大数据产生的地方都需要图计算，现在的图处理基本都是分布式的图处理，而并非单机处理。Spark GraphX由于底层是基于Spark来处理的，所以天然就是一个分布式的图处理系统。

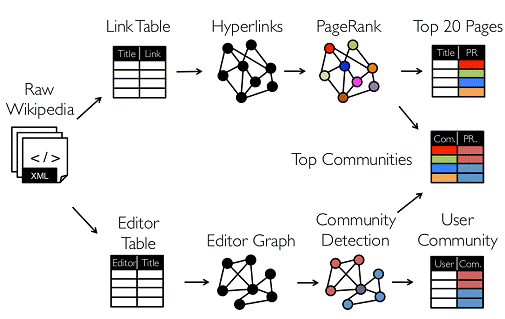
图的分布式或者并行处理其实是把图拆分成很多的子图，然后分别对这些子图进行计算，计算的时候可以分别迭代进行分阶段的计算，即对图进行并行计算。下面我们看一下图计算的简单示例：

从图中我们可以看出：拿到Wikipedia的文档以后，可以变成Link Table形式的视图，然后基于Link Table形式的视图可以分析成Hyperlinks超链接，最后我们可以使用PageRank去分析得出Top Communities。在下面路径中的Editor Graph到Community，这个过程可以称之为Triangle Computation，这是计算三角形的一个算法，基于此会发现一个社区。从上面的分析中我们可以发现图计算有很多的做法和算法，同时也发现图和表格可以做互相的转换。

 

2.     GraphX的框架

 设计GraphX时，点分割和GAS都已成熟，在设计和编码中针对它们进行了优化，并在功能和性能之间寻找最佳的平衡点。如同Spark本身，每个子模块都有一个核心抽象。GraphX的核心抽象是Resilient Distributed Property Graph，一种点和边都带属性的有向多重图。它扩展了Spark RDD的抽象，有Table和Graph两种视图，而只需要一份物理存储。两种视图都有自己独有的操作符，从而获得了灵活操作和执行效率。

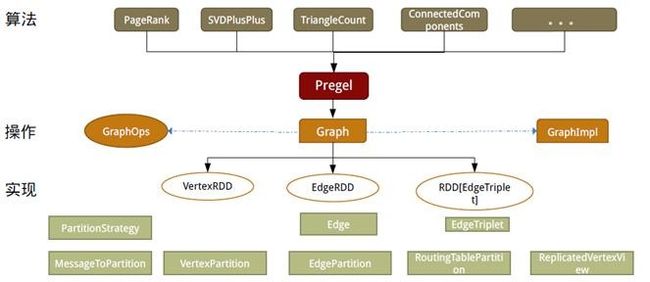
如同Spark，GraphX的代码非常简洁。GraphX的核心代码只有3千多行，而在此之上实现的Pregel模式，只要短短的20多行。GraphX的代码结构整体下图所示，其中大部分的实现，都是围绕Partition的优化进行的。这在某种程度上说明了点分割的存储和相应的计算优化，的确是图计算框架的重点和难点。

2.1.1图存储模式

l边分割（Edge-Cut）：每个顶点都存储一次，但有的边会被打断分到两台机器上。这样做的好处是节省存储空间；坏处是对图进行基于边的计算时，对于一条两个顶点被分到不同机器上的边来说，要跨机器通信传输数据，内网通信流量大。

l点分割（Vertex-Cut）：每条边只存储一次，都只会出现在一台机器上。邻居多的点会被复制到多台机器上，增加了存储开销，同时会引发数据同步问题。好处是可以大幅减少内网通信量。

 

2.1.2GraphX存储模式

Graphx借鉴PowerGraph，使用的是Vertex-Cut(点分割)方式存储图，用三个RDD存储图数据信息：

lVertexTable(id, data)：id为Vertex id，data为Edge data

lEdgeTable(pid, src, dst, data)：pid为Partion id，src为原定点id，dst为目的顶点id

lRoutingTable(id, pid)：id为Vertex id，pid为Partion id

点分割存储实现如下图所示：

 

2.1.3图计算模式

    目前基于图的并行计算框架已经有很多，比如来自Google的Pregel、来自Apache开源的图计算框架Giraph/HAMA以及最为著名的GraphLab，其中Pregel、HAMA和Giraph都是非常类似的，都是基于BSP（Bulk Synchronous Parallell）模式。

BulkSynchronous Parallell，即整体同步并行，它将计算分成一系列的超步（superstep）的迭代（iteration）。从纵向上看，它是一个串行模式，而从横向上看，它是一个并行的模式，每两个superstep之间设置一个栅栏（barrier），即整体同步点，确定所有并行的计算都完成后再启动下一轮superstep。

每一个超步（superstep）包含三部分内容：

1.计算compute：每一个processor利用上一个superstep传过来的消息和本地的数据进行本地计算；

2.消息传递：每一个processor计算完毕后，将消息传递个与之关联的其它processors

3.整体同步点：用于整体同步，确定所有的计算和消息传递都进行完毕后，进入下一个superstep。

3.GraphX实例

3.1 图例演示

3.1.1 例子介绍

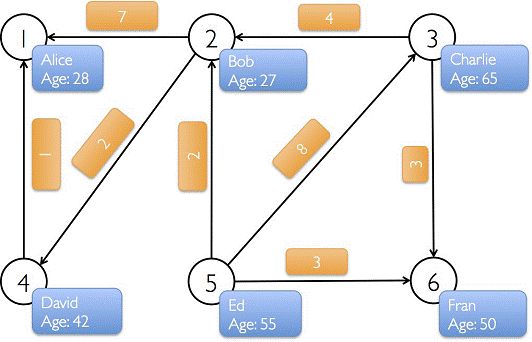
下图中有6个人，每个人有名字和年龄，这些人根据社会关系形成8条边，每条边有其属性。在以下例子演示中将构建顶点、边和图，打印图的属性、转换操作、结构操作、连接操作、聚合操作，并结合实际要求进行演示。

3.1.2 程序代码

import org.apache.log4j.{Level, Logger} import org.apache.spark.{SparkContext, SparkConf} import org.apache.spark.graphx._ import org.apache.spark.rdd.RDD   object GraphXExample {   def main(args: Array[String]) {     //屏蔽日志     Logger.getLogger("org.apache.spark").setLevel(Level.WARN)     Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)       //设置运行环境     val conf = new SparkConf().setAppName("SimpleGraphX").setMaster("local")     val sc = new SparkContext(conf)       //设置顶点和边，注意顶点和边都是用元组定义的Array     //顶点的数据类型是VD:(String,Int)     val vertexArray = Array(       (1L, ("Alice", 28)),       (2L, ("Bob", 27)),       (3L, ("Charlie", 65)),       (4L, ("David", 42)),       (5L, ("Ed", 55)),       (6L, ("Fran", 50))     )     //边的数据类型ED:Int     val edgeArray = Array(       Edge(2L, 1L, 7),       Edge(2L, 4L, 2),       Edge(3L, 2L, 4),       Edge(3L, 6L, 3),       Edge(4L, 1L, 1),       Edge(5L, 2L, 2),       Edge(5L, 3L, 8),       Edge(5L, 6L, 3)     )       //构造vertexRDD和edgeRDD     val vertexRDD: RDD[(Long, (String, Int))] = sc.parallelize(vertexArray)     val edgeRDD: RDD[Edge[Int]] = sc.parallelize(edgeArray)       //构造图Graph[VD,ED]     val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)       //***********************************************************************************     //***************************  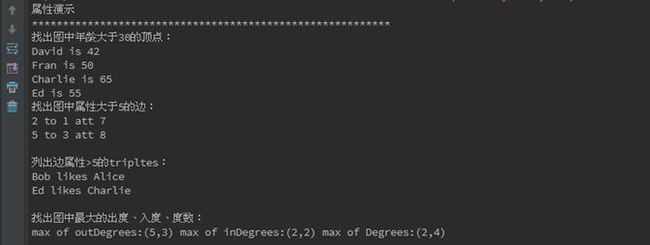图的属性    ****************************************     //**********************************************************************************         println("***********************************************")     println("属性演示")     println("**********************************************************")     println("找出图中年龄大于30的顶点：")     graph.vertices.filter { case (id, (name, age)) => age > 30}.collect.foreach {       case (id, (name, age)) => println(s"$name is $age")     }       //边操作：找出图中属性大于5的边     println("找出图中属性大于5的边：") graph.edges.filter(e => e.attr > 5).collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))     println       //triplets操作，((srcId, srcAttr), (dstId, dstAttr), attr)     println("列出边属性>5的tripltes：")     for (triplet <- graph.triplets.filter(t => t.attr > 5).collect) {       println(s"${triplet.srcAttr._1} likes ${triplet.dstAttr._1}")     }     println       //Degrees操作     println("找出图中最大的出度、入度、度数：")     def max(a: (VertexId, Int), b: (VertexId, Int)): (VertexId, Int) = {       if (a._2 > b._2) a else b     }     println("max of outDegrees:" + graph.outDegrees.reduce(max) + " max of inDegrees:" + graph.inDegrees.reduce(max) + " max of Degrees:" + graph.degrees.reduce(max))     println         //***********************************************************************************     //***************************  转换操作    ****************************************     //**********************************************************************************       println("**********************************************************")     println("转换操作")     println("**********************************************************")     println("顶点的转换操作，顶点age + 10：")     graph.mapVertices{ case (id, (name, age)) => (id, (name, age+10))}.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))     println     println("边的转换操作，边的属性*2：")     graph.mapEdges(e=>e.attr*2).edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))     println           //***********************************************************************************     //***************************  结构操作    ****************************************     //**********************************************************************************      println("**********************************************************")     println("结构操作")     println("**********************************************************")     println("顶点年纪>30的子图：")     val subGraph = graph.subgraph(vpred = (id, vd) => vd._2 >= 30)     println("子图所有顶点：")     subGraph.vertices.collect.foreach(v => println(s"${v._2._1} is ${v._2._2}"))     println     println("子图所有边：")     subGraph.edges.collect.foreach(e => println(s"${e.srcId} to ${e.dstId} att ${e.attr}"))     println              //***********************************************************************************     //***************************  连接操作    ****************************************     //**********************************************************************************      println("**********************************************************")     println("连接操作")     println("**********************************************************")     val inDegrees: VertexRDD[Int] = graph.inDegrees     case class User(name: String, age: Int, inDeg: Int, outDeg: Int)       //创建一个新图，顶点VD的数据类型为User，并从graph做类型转换     val initialUserGraph: Graph[User, Int] = graph.mapVertices { case (id, (name, age)) => User(name, age, 0, 0)}       //initialUserGraph与inDegrees、outDegrees（RDD）进行连接，并修改initialUserGraph中inDeg值、outDeg值     val userGraph = initialUserGraph.outerJoinVertices(initialUserGraph.inDegrees) {       case (id, u, inDegOpt) => User(u.name, u.age, inDegOpt.getOrElse(0), u.outDeg)     }.outerJoinVertices(initialUserGraph.outDegrees) {       case (id, u, outDegOpt) => User(u.name, u.age, u.inDeg,outDegOpt.getOrElse(0))     }       println("连接图的属性：") userGraph.vertices.collect.foreach(v => println(s"${v._2.name} inDeg: ${v._2.inDeg}  outDeg: ${v._2.outDeg}"))     println       println("出度和入读相同的人员：")     userGraph.vertices.filter {       case (id, u) => u.inDeg == u.outDeg     }.collect.foreach {       case (id, property) => println(property.name)     }     println          //***********************************************************************************     //***************************  聚合操作    ****************************************     //**********************************************************************************      println("**********************************************************")     println("聚合操作")     println("**********************************************************")     println("找出年纪最大的追求者：")     val oldestFollower: VertexRDD[(String, Int)] = userGraph.mapReduceTriplets[(String, Int)](       // 将源顶点的属性发送给目标顶点，map过程       edge => Iterator((edge.dstId, (edge.srcAttr.name, edge.srcAttr.age))),       // 得到最大追求者，reduce过程       (a, b) => if (a._2 > b._2) a else b     )       userGraph.vertices.leftJoin(oldestFollower) { (id, user, optOldestFollower) =>       optOldestFollower match {         case None => s"${user.name} does not have any followers."         case Some((name, age)) => s"${name} is the oldest follower of ${user.name}."       }     }.collect.foreach { case (id, str) => println(str)}     println        //***********************************************************************************     //***************************  实用操作    ****************************************     //**********************************************************************************     println("**********************************************************")     println("聚合操作")     println("**********************************************************")     println("找出5到各顶点的最短：")     val sourceId: VertexId = 5L // 定义源点     val initialGraph = graph.mapVertices((id, _) => if (id == sourceId) 0.0 else Double.PositiveInfinity)     val sssp = initialGraph.pregel(Double.PositiveInfinity)(       (id, dist, newDist) => math.min(dist, newDist),       triplet => {  // 计算权重         if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {           Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))         } else {           Iterator.empty         }       },       (a,b) => math.min(a,b) // 最短距离     )     println(sssp.vertices.collect.mkString("\n"))       sc.stop()   } }