并查集

一，并查集

说通俗点就是两个东西之间的连通器
例题嘛
HDU1232畅通工程
洛谷3367并查集
简单来说并查集也没什么，就是两个函数，一个是查找（找一个东西的祖先），另一个是合并（相当于两个人结为姻亲）

查找函数

注意：这里a【】数组是开在全局变量中的 而写在主函数中初始化为i也就是 a[i]=i 就是他自己跟他自己

int a[10000];
int find(int n){
	int r=n;
	while(r!=a[r]){
		r=a[r];
	}
	//路径压缩，有些题用不上下面有个图可以帮助理解
	int i=n,j;
	while(i!=r){//就是把每个点都连在根节点上； 
		j=a[i];
		a[i]=r;
		i=j;
	} 
	return r;
}

看一下这个图会帮组你理解不

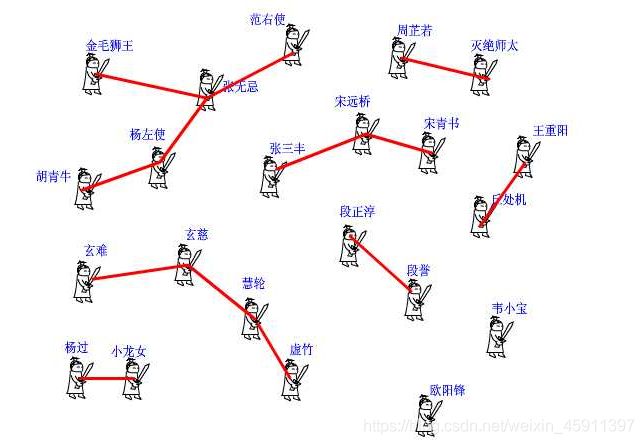
这个算是查找到图解吧其实也是合并的图解。

路径优化

也就是这一块代码：

	int i=n,j;
	while(i!=r){//就是把每个点都连在根节点上； 
		j=a[i];
		a[i]=r;
		i=j;
	} 

有时候查找会超时很大一部分原因是因为查找的结点太多，而路径优化之后 则不同他是直接一步就能找到根节点
如下图 就是将前面打的那种情况转换成后面那种，这样找起来就近但多了
例如 要找白面葫芦娃的根节点 ，首先找到六组长 ，再找到三营长，再找到曹公公，而路径压缩后就是右边这种，直接找到曹公公。这是数据量比较少，要是多了那。可见路径压缩可以解决一定的超时问题。

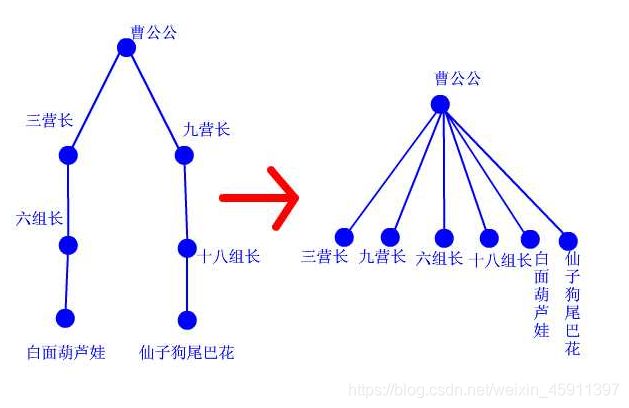
合并：

简单的来书就是把这两个数或者他们的祖先连起来

void add(int x,int y){
	int fx=find(x),fy=find(y);//找到他们各自的根节点 
	if(fx!=fy)//确保他们原本没连着
	a[fx]=fy;//将他们连起来
	//如果他们已经连起来了就没必要了 
} 

例题解读

畅通工程

Problem Description
某省调查城镇交通状况，得到现有城镇道路统计表，
表中列出了每条道路直接连通的城镇。
省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通
（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。
问最少还需要建设多少条道路？

Input
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，
分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，
每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。
为简单起见，城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。


Output
对每个测试用例，在1行里输出最少还需要建设的道路数目。


Sample Input
4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0


Sample Output
1
0
2
998

Hint
Hint

Huge input, scanf is recommended.

题意理解
简单的并查集问题

#include
#include
#include
#include
#include 
#include 
#define ll long long int
const int mod=998244353;
using namespace std;
const int inf=1e9+7;
const int maxn=1e5+10;

ll n ,k,m,x,y,sum,l,r,t,p;
ll  a[maxn],b[maxn];
ll dp[101][101];
char str[maxn];

int find(int n){
	int r=n;
	while(r!=a[r]){
		r=a[r];
	}
	//路径压缩，有些题用不上下面有个图可以帮助理解
	int i=n,j;
	while(i!=r){//就是把每个点都连在根节点上； 
		j=a[i];
		a[i]=r;
		i=j;
	} 
	return r;
}

void add(int x,int y){
	int fx=find(x),fy=find(y);//找到他们各自的根节点 
	if(fx!=fy)//确保他们原本没连着
	a[fx]=fy;//将他们连起来
	//如果他们已经连起来了就没必要了 
} 

int main(){
	while(cin>>n&&n){
		cin>>m;
		sum=0;
		for(int i=1;i<=n;i++)
			a[i]=i;
		for(int i=1;i<=n;i++)//注意这里要清负责下次进入是可能会出错
			b[i]=0;
		for(int i=1;i<=m;i++)
		{
			cin>>x>>y;
			add(x,y);	
		}	
		for(int i=1;i<=n;i++)	
			b[find(a[i])]++;
		for(int i=1;i<=n;i++)
			if(b[i]!=0) sum++;
		cout<<sum-1<<endl;//有n个点独立 则用n-1条边链接即可；
	}
	return 0;
}