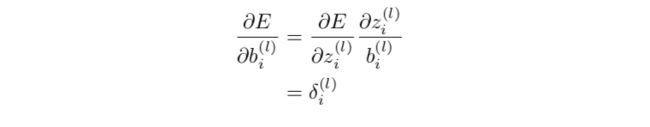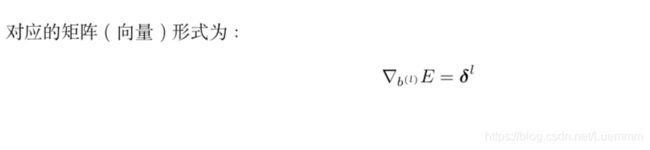理解dropout,梯度下降,反向传播算法
1. Dropout出现的原因
在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:模型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低。
过拟合是很多机器学习的通病。如果模型过拟合,那么得到的模型几乎不能用。为了解决过拟合问题,一般会采用模型集成的方法,即训练多个模型进行组合。此时,训练模型费时就成为一个很大的问题,不仅训练多个模型费时,测试多个模型也是很费时。
综上所述,训练深度神经网络的时候,总是会遇到两大缺点:
(1)容易过拟合
(2)费时
Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果。
2.什么是dropout
Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中,通过忽略一半的特征检测器(让一半的隐层节点值为0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
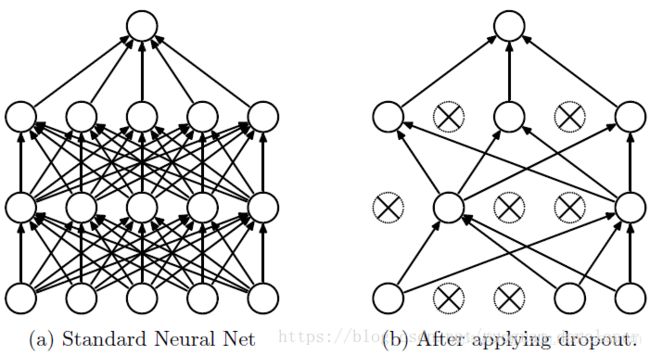
Dropout说的简单一点就是:我们在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征,如图1所示。
3.dropout流程
对于全连接网络,输入是x输出是y,正常的流程是:我们首先把x通过网络前向传播,然后把误差反向传播以决定如何更新参数让网络进行学习。
使用Dropout之后,过程变成如下:
(1)首先随机(临时)删掉网络中一半的隐藏神经元,输入输出神经元保持不变(图3中虚线为部分临时被删除的神经元)
(2) 然后把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)。
(3)然后继续重复这一过程:
. 恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
. 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉(备份被删除神经元的参数)。
. 对一小批训练样本,先前向传播然后反向传播损失并根据随机梯度下降法更新参数(w,b) (没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)。
4. 为什么说Dropout可以解决过拟合?
(1)取平均的作用: 先回到标准的模型即没有dropout,我们用相同的训练数据去训练5个不同的神经网络,一般会得到5个不同的结果,此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9,其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
(2)减少神经元之间复杂的共适应关系: 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
(3)Dropout类似于性别在生物进化中的角色:物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。
5.随机梯度下降
- 梯度下降的用处
在机器学习算法中,有时候需要对原始的模型构建损失函数,然后通过优化算法对损失函数进行优化,以便寻找到最优的参数,使得损失函数的值最小。而在求解机器学习参数的优化算法中,使用较多的就是基于梯度下降的优化算法(Gradient Descent, GD)。
优点:效率。在梯度下降法的求解过程中,只需求解损失函数的一阶导数,计算的代价比较小,可以在很多大规模数据集上应用。
缺点:求解的是局部最优值,即由于方向选择的问题,得到的结果不一定是全局最优步长选择,过小使得函数收敛速度慢,过大又容易找不到最优解。
- 梯度下降的变形形式
根据处理的训练数据的不同,主要有以下三种形式:
1)批量梯度下降法BGD(Batch Gradient Descent):
针对的是整个数据集,通过对所有的样本的计算来求解梯度的方向。
优点:全局最优解;易于并行实现;
缺点:当样本数据很多时,计算量开销大,计算速度慢
2)小批量梯度下降法MBGD(mini-batch Gradient Descent)
把数据分为若干个批,按批来更新参数,这样,一个批中的一组数据共同决定了本次梯度的方向,下降起来就不容易跑偏,减少了随机性
优点:减少了计算的开销量,降低了随机性
3)随机梯度下降法SGD(stochastic gradient descent)
每个数据都计算算一下损失函数,然后求梯度更新参数。
优点:计算速度快
缺点:收敛性能不好
总结:SGD可以看作是MBGD的一个特例,及batch_size=1的情况。在深度学习及机器学习中,基本上都是使用的MBGD算法。
6.误差反向传播算法
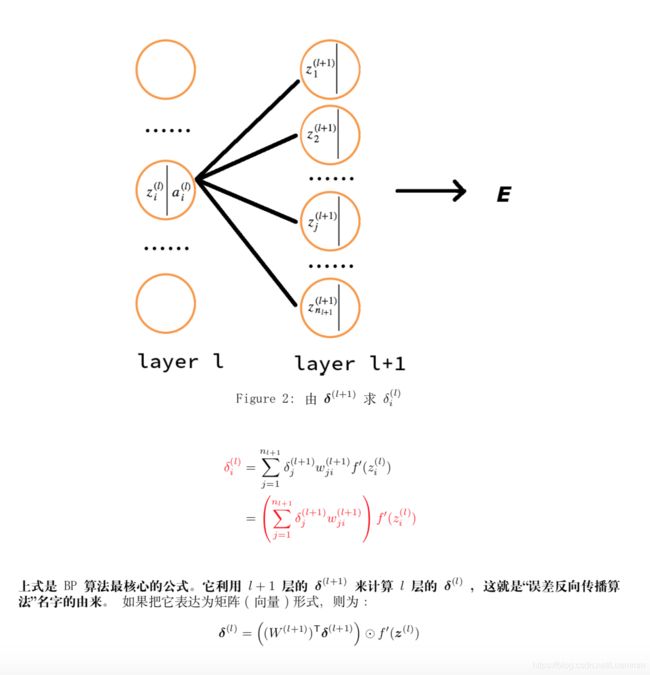
误差反向传播算法简称反向传播算法(即BP算法)。使用反向传播算法的多层感知器又称为BP神经网络。BP算法是一个迭代算法,它的基本思想为:(1)先计算每一层的状态和激活值,直到最后一层(即信号是前向传播的);(2)计算每一层的误差,误差的计算过程是从最后一层向前推进的(这就是反向传播算法名字的由来);(3)更新参数(目标是误差变小)。迭代前面两个步骤,直到满足停止准则(比如相邻两次迭代的误差的差别很小)。
- 代价函数
- 梯度下降方法
- 反向传播公式推导
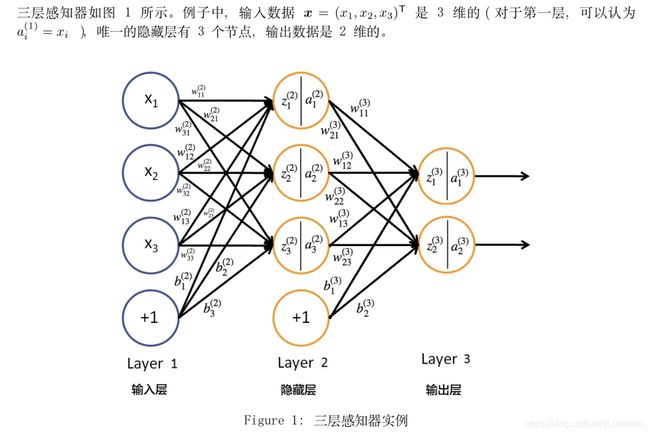
以三层感知器为例,本文中记号说明:
信息前向传播:
误差反向传播:
输出层的权值更新:
隐藏层的权重更新:
输出层和隐藏层的偏置参数更新:
反向传播算法的四个核心公式:
反向传播算法计算某个训练数据的代价函数对参数的偏导数:
算法总结:批量梯度下降算法更新参数:
梯度消失问题及解决办法: