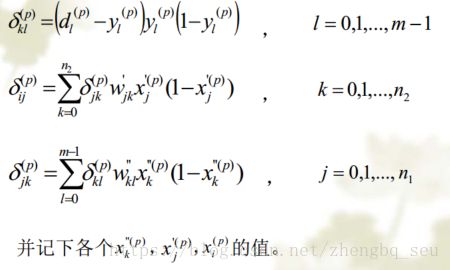神经网络课程(上)
自存。PDF 下载链接
第一讲 基本的神经元模型
1)神经元模型
最简单的MP模型,右图是“与”逻辑的数学表达:
神经元模型 基函数表示“如何组合” 激活函数表示“是否到阈值”“最后网络表达的方式”
基函数类型1:线性函数 基函数类型2:距离函数
激活函数类型:1)硬极限函数(sgn,大于0为1,否则为0);2)线性函数(常用于实现函数逼近的神经网络的输出层神经元。作为隐层神经元的激活函数时,线性函数常用于理论分析);3)饱和线性函数 (饱和激活函数也常用于分类。缺点:多个饱和线性函数前后互联时,会导致神经网络系统分析困难 );4)Sigmoidal函数 (也叫 S函数,是一类非常重要的激活函数,无论神经网络用于分类、函数逼近或优化, Sigmoidal函数都是常用的激活函数。表达式1/(1+ exp(- lenta u));5)径向基函数(极为重要的一类激活函数,常用于径向基函数神经网络(RBF网络))。 (不放图了 太占地方)
2)神经元学习算法
(1)Hebb学习规则是一种无导学习算法 ,Hebb规则说明:使用频繁的突触联系会变得更紧密,从而可理解为突触的特点是用进废退。除了上基本Hebb学习规则,根据应用的不同,还有Oja和Karhunenn的非线性Hebb学习算法。Hebb学习规则常用于自组织网络或特征提取网络。![]()
(2)离散感知器学习规则: 如果神经元的基函数取线性函数,激活函数取硬极限函数,则神经元就成了单神经元感知器(离散感知器)。单神经元感知器的学习规则称离散感知器学习规则,是一种有导学习算法 。
(3)δ学习规则也称梯度法或最速下降法,是最常用的神经网络学习算法。 δ学习规则是一种有导学习算法。
(4)Widrow-Hoff学习规则也是一种有导学习算法。 Widrow-Hoff学习规则常用于自适应线性单元(Adaline) 我觉得就是基函数确定为线性函数的δ学习规则而已
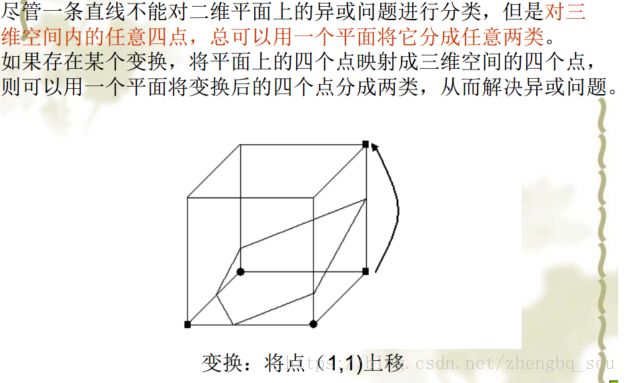
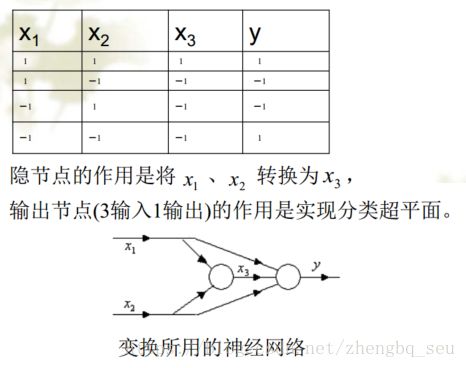
3)单个神经元解决问题的能力
以“异或问题”为例,
第二讲 多层感知器网络
权值修改中的一个改变学习速率的好算法 ![]() “一次到位”算法 或许可以加快收敛速度?
“一次到位”算法 或许可以加快收敛速度?
第三讲 BP算法
BP网与线性阈值单元组成的多层感知器网络结构完全相同,只是各隐节点的激活函数使用了第二章介绍的Sigmoidal函数,所以BP网也称隐节点激活函数采用Sigmoidal函数的多层感知器。 BP网输出节点的激活函数根据应用的不同而异:如果多层感知器用于分类,则输出层节点一般用Sigmoidal函数或硬极限函数;如果多层感知器用于函数逼近,则输出层节点应该用线性函数。
BP算法也称误差反向传播算法(Error Back-propagationAlgorithm) ,是一类有导学习算法,用于BP网的权值和阈值
学习。具体过程见PPT,详细推导过程已推导过一遍,具体的一个计算也已经计算过,除了某个正负号是错的,其余都没有问题。BP算法的各步骤:(可以参考第10章的灵敏度剪枝算法)
. 有关BP网和BP算法的讨论
| 样本预处理 | |
| 增量学习和批学习 | 批处理时, 不存在输入模式次序问题,算法稳定性好,是有平均效应的梯度下降法, 一般取较小 值; 增量处理适合于在线处理,但要求训练模式输入有足够的随机性,而且增量处理对输入模式的噪声 比较敏感,即对剧烈变化的输入模式,效果较差。 |
| 激励函数 | 另外,神经元函数的斜率由 大,权值的调节量就越大。用可变的λ可摆脱局部极小点。但大的λ值相当于大 此不如固定λ ,只调节 |
| 误差函数的选择 | 对BP网而言,网络的初始权值不同,每次训练的结果也不同,这是由于误差曲面的局部最小点非 常多, BP算法本质上是梯度算法,易陷入局部最小点。一般情况下,网络的初始权值要取小的随 机值, 既保证各神经元的输入 u值较小,工作在激励函数斜率变化最大的区域,也防止多次连续学 习后,某些权值的绝对值不合理的无限增长。 |
| 学习率(步长) |
一般要求是,当训练到误差曲面得平坦区时,为加快收敛应使 烈区时,为防止过学习(使误差增加),应使 步长算法。 还要注意到,小的 |
介绍一些避免局部最小和提高收敛速度的改进方法 :
第四讲 径向基函数神经网络 (RBF)
4.1 结构和工作原理

意味着如果神经网络有较大的输出,必定激活了一个或多个隐节点。
4.2 RBF网的数学基础
内插问题(引出改进方案——正则化网络)只要输入样本的X不相同,隐层输出阵H的可逆性是可以保证的。因此,如果把全部样本输入作为RBF网的数据中心,网络
在样本输入点的输出就等于教师信号,此时网络对样本实现了完全内插,即对所有样本误差为0。但上式方案存在以下问题:
(1). 通常情况下,样本数据较多,即N数值较大,上述方案中隐层输出阵H的条件数可能过大,求逆时可能导致不稳定。
(2). 如果样本输出含有噪声,此时由于存在过学习的问题,作完全内插是不合适的,而对数据作逼近可能更合理。
为了解决这些问题,可以采用下面的正则化网络。
4.3 RBF网的常用学习算法
正则化网络要求网络的隐节点数等于训练样本数,在训练样本较多时该方法显然不能令人满意,因此有必要寻找更适合
工程化应用的RBF网学习方法。给定了训练样本, RBF网的学习算法应该解决以下问题:结构设计,即如何确定网络隐节点数h;确定各径向基函数的数据中心c及扩展常数 ;输出权值修正。一般情况下,如果知道了网络的隐节点数、数据中心和扩展常数, RBF网从输入到输出就成了一个线性方程组,此时权值学习可采用最小二乘法求解。
根据数据中心的取值方法, RBF网的设计方法可分为两大类。
1) 数据中心从样本输入中选取
这种方法中数据中心从样本输入中选,如OLS算法、 ROLS算法、进化优选算法等。这类算法的特点是数据中心一旦获得便不再改变,而隐节点的数目或者一开始就固定,或者在学习过程中动态调整。
2) 数据中心动态调节方法
这类方法中数据中心的位置在学习过程中是动态调节的,如两步法(先基于这类方法中数据中心的位置在学习过程中是动态调节的,如两步法(先基于K-means等聚类算法确定隐层参数,然后确定输出层权参数)、梯度训练方法、正交最小二乘(OLS)算法、三步法、资源分配网络(RAN)等。
这些方法各有优缺点。第一类算法较容易实现,且能在权值学习的同时确定隐节点的数目,并保证学习误差不大于给定值,但数据中心从样本输入中选取是否合理,值得进一步讨论。另外, OLS算法并不一定能设计出具有最小结构的RBF网,也无法确定基函数的扩展常数。
第二类方法中,聚类方法的优点是能根据各聚类中心之间的距离确定各隐节点的扩展常数,缺点是确定数据中心时只用到了样本输入信息,而没有用到样本输出信息;另外聚类方法也无法确定聚类的数目 (RBF网的隐节点数)。由于RBF网的隐节点数对其泛化能力有极大的影响,所以寻找能确定聚类数目的合理方法,是聚类方法设计RBF网时需首先解决的问题。
4.3.1 两步法
最经典的RBF网学习,算法思路是先用无监督学习(用k-means算法对样本输入进行聚类)方法确定RBF网中h个隐节点的数据中心,并根据各数据中心之间的距离确定隐节点的扩展常数,然后用有监督学习(梯度法)训练各隐节点的输出权值。
4.3.2 梯度训练方法
RBF网的梯度训练方法[Hayk2001]与BP算法训练多层感知器的原理类似,也是通过最小化目标函数实现对各隐节点数据中心、扩展常数和输出权值的调节。(书里给出一种带遗忘因子的单输出RBF网学习方法)(对所有参数进行求解)
4.3.3 三步法 (很朴素 但很有效的思想)
4.3.4 正交最小二乘(OLS)学习算法 (很机智的想法)
能量贡献的计算原理 就不提了,一个基本原理是H的列被选择的越多,能量贡献得越多,误差越小。(简单的原理,复杂的或者说是科学的表达方式,写论文的时候参考)
正交最小二乘算法(OLS)对H的列的选择是在对H作Gram-Schmidt正交化的过程中实现的。 最小夹角具有最大贡献(夹角指的是输出数据矢量y 与H的N个列向量 的夹角)
一种方法是取固定值,但值的大小要通过凑试方法( Try and Error )确定;另一种方法是聚类。聚类方法能根据各聚类中心之间的距离确定各隐节点的扩展常数,缺点是确定数据中心时只用到了样本输入信息,而没有用到样本输出信息或误差信息;另外聚类方法也无法确定聚类的数目